近端策略优化 (Proximal policy optimization, PPO)：强化学习中的一种策略优化方法，其相比 TRPO 更简单、稳定与高效。

1 重要性采样的局限

上一篇文章策略梯度算法尾部提到了从 On-Policy 转换到 Off-Policy 的方法，从数学上看起来这个转换是无损的，但在实际情况中它是有代价的。

例如对于以下例子，蓝色为 $p(x)$，红色为 $q(x)$，绿色是 $f(x)$.

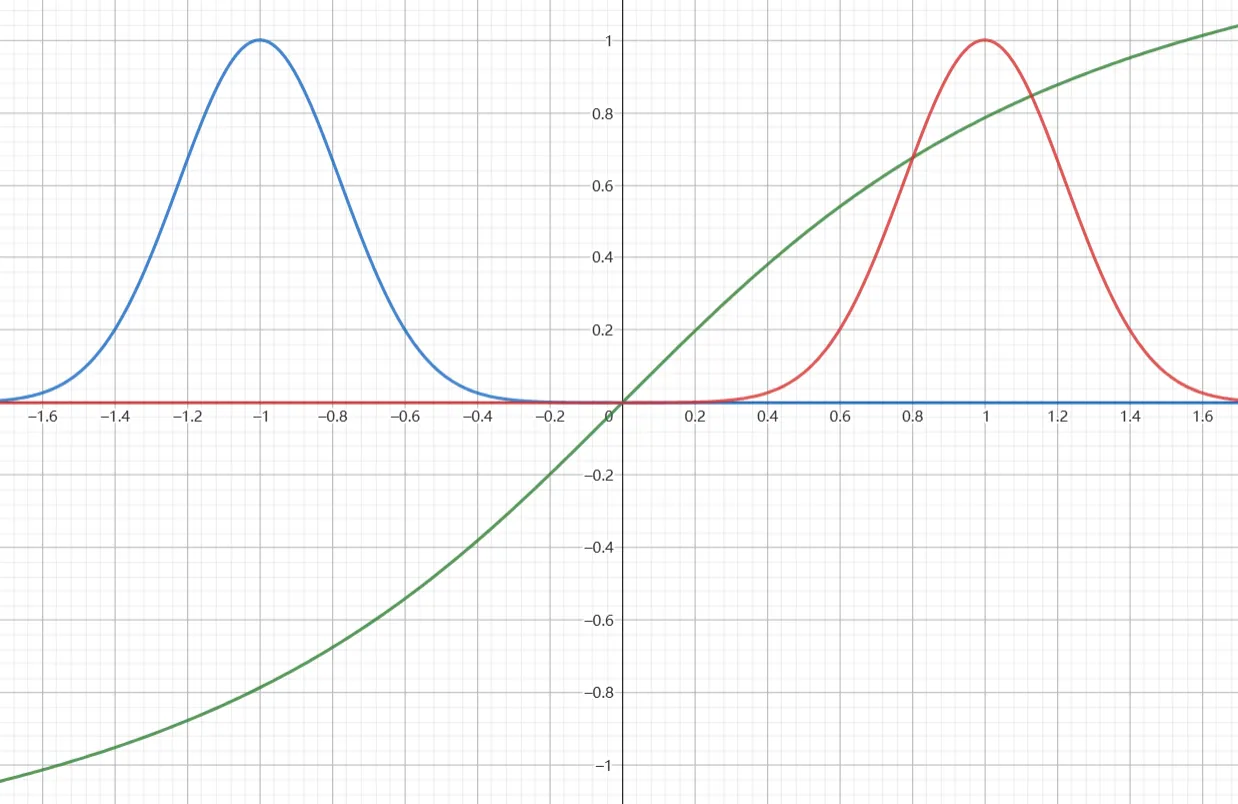
显然，$\mathbb{E}_{x\sim p}[f(x)]<0$，那根据重要性采样：

$$ \mathbb{E}_{x\sim p}[f(x)]=\mathbb{E}_{x\sim q}[\frac{p(x)}{q(x)}f(x)]<0 $$

这在数学上当然是成立的，但实际中需要考虑的是采样数量是有限的。

很有可能我们在 $q$ 分布中采样得到的 $x$ 全部都是 $>0$ 的，这就会导致算出 $\mathbb{E}_{x\sim p}[f(x)]>0$ 的错误结果。只有采样数量足够多（或者运气够好），采到 $x<0$ 的情况，才有可能得到更加正确的结果。

这便告诉我们，即使重要性采样在数学中是完全正确的，但在实际中需要保证 $p,q$ 两分布的差异不要太大，过大的差距会导致采样得到的期望有很大的偏差。

2 添加约束

首先来看重要性采样的策略梯度算法的目标：

$$ \max_{\theta}\mathbb{E}_{(s_t,a_t)\sim\pi_{\theta'}}\left[\frac{p_{\theta}(a_t\mid s_t)}{p_{\theta'}(a_t\mid s_t)}A^{\theta'}(s_t,a_t)\right] $$

最朴素的想法是添加一个约束条件，不要让 $\pi_{\theta}$ 和 $\pi_{\theta'}$ 两个分布差异太大：

$$ \begin{align} \max_{\theta}\ &\mathbb{E}_{(s_t,a_t)\sim\pi_{\theta'}}\left[\frac{p_{\theta}(a_t\mid s_t)}{p_{\theta'}(a_t\mid s_t)}A^{\theta'}(s_t,a_t)\right]\\ \text{s.t. }\ &\mathbb{E}[\mathrm{KL}[\pi_{\theta}(\cdot\mid s_t),\pi_{\theta'}(\cdot\mid s_t)]]\leq\delta \end{align} $$

这个最朴素的思想便是 TRPO (Trust Region Policy Optimization) 方法了，不过带约束的问题较难求解，将硬约束转换为惩罚值，把问题变成无约束的来求解更方便：

$$ \max_{\theta}\ \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta'}}\left[\frac{p_{\theta}(a_t\mid s_t)}{p_{\theta'}(a_t\mid s_t)}A^{\theta'}(s_t,a_t)-\beta\;\mathrm{KL}[\pi_{\theta}(\cdot\mid s_t),\pi_{\theta'}(\cdot\mid s_t)]\right] $$

但这又带来一个问题，$\beta$ 这个超参数的选择较为困难。很难选择一个适应于多种问题的 $\beta$，甚至在单一的问题求解中，设定固定的 $\beta$ 也表现不佳。

3 PPO 方法

在 PPO 的论文中，提出了两种方法，分别是：

  1. 截断代理目标 (Clipped Surrogate Objective)
  2. 自适应 KL 惩罚系数 (Adaptive KL Penalty Coefficient)

3.1 截断代理目标

这种方法的目标是：

$$ \max_{\theta}\ \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta'}}\left[\min\left(\frac{p_{\theta}(a_t\mid s_t)}{p_{\theta'}(a_t\mid s_t)}A^{\theta'}(s_t,a_t),\mathrm{clip}\left(\frac{p_{\theta}(a_t\mid s_t)}{p_{\theta'}(a_t\mid s_t)},1-\epsilon,1+\epsilon\right)A^{\theta'}(s_t,a_t)\right)\right] $$

其中：

$$ \mathrm{clip}(x,y,z)= \begin{align} \begin{cases} y&,\text{if}\;x<y\\ x&,\text{if}\;y\leq x\leq z\\ z&,\text{if}\;x>z\\ \end{cases} \end{align} $$

这个公式看着花里胡哨的，那就先看期望值里面的内容，画个图出来就好理解了。左边是 $A>0$ 的情况，右边是 $A<0$ 的情况：

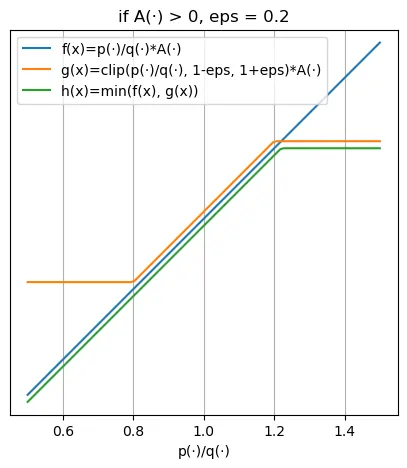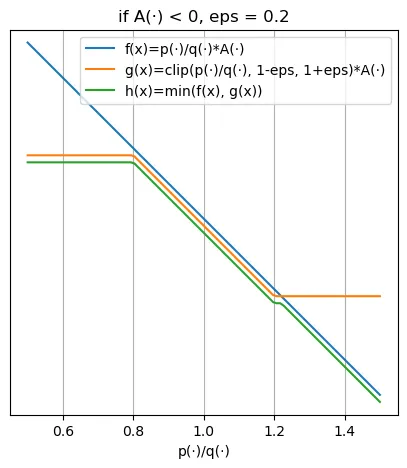对于 $A>0$ 的情况，学习时会设法通过变大 $p_{\theta}(a_t\mid s_t)$ 这个概率来最大化期望，但是变大 $p_{\theta}(a_t\mid s_t)$ 同时会导致 $\frac{p_{\theta}(a_t\mid s_t)}{p_{\theta'}(a_t\mid s_t)}$ 变大。当这个比值大于设定的 $1+\epsilon$ 后，目标函数值将会被截断，“告诉”模型再往上调整也不会获得收益了。反之，对于 $A<0$ 的情况也是一样的，就是加了个负号而已。

可以看到，这个方法的思路实际上很直白，就是通过限制模型通过加大 $\theta$ 和 $\theta'$ 的差距获得的收益，来维持两个分布相似。

3.2 自适应 KL 惩罚系数

这种方法实际上就是让带惩罚的 TRPO 方法的惩罚值可以自适应，它的目标和上文一模一样：

$$ \max_{\theta}\ \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta'}}\left[\frac{p_{\theta}(a_t\mid s_t)}{p_{\theta'}(a_t\mid s_t)}A^{\theta'}(s_t,a_t)-\beta\;\mathrm{KL}[\pi_{\theta}(\cdot\mid s_t),\pi_{\theta'}(\cdot\mid s_t)]\right] $$

唯一区别就是 $\beta$ 会进行自适应。首先设定一个目标差异 $d_{\text{target}}$：

  • 计算 $d=\mathbb{E}[\mathrm{KL}[\pi_{\theta}(\cdot\mid s_t),\pi_{\theta'}(\cdot\mid s_t)]]$

    • 如果 $d<\frac{d_{\text{target}}}{1.5}$，则 $\beta\leftarrow\frac{\beta}{2}$
    • 如果 $d>1.5\;d_{\text{target}}$，则 $\beta\leftarrow2\beta$

其中的超参数 $1.5$ 和 $2$ 是启发式选取得到的，但这个算法实际上对这两个超参不敏感。

这个方法的思路实际上也很直白：如果我们发现 $\theta$ 和 $\theta'$ 的差距太小，这代表 $\beta$ 的限制可能太大了，模型不愿意去调整 $\theta$ 的分布，于是将 $\beta$ 改小；如果发现 $\theta$ 和 $\theta'$ 的差距太大，这代表 $\beta$ 的限制不够，于是将 $\beta$ 改大。

4 效果

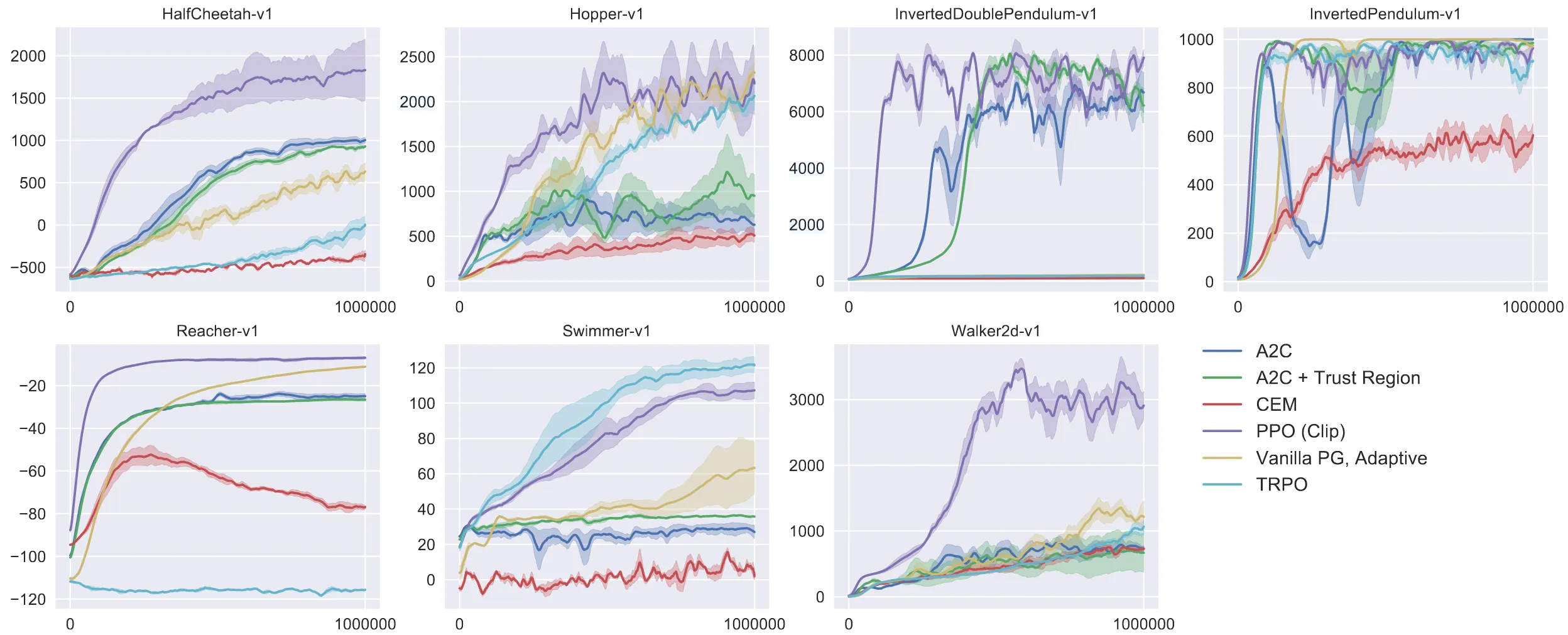
论文中将各种策略优化方法进行了对比实验，可以看到使用 Clip 方法的 PPO 算法在大多数场景下都优于其他算法。可以看到 PPO 算法的思路虽然朴素直白，但是效果是非常不错的。

5 Critic 模型的引入

在看了 PPO 相关的论文和博文后，我发现目前应用的 PPO 并不是原论文的原始版本。

原论文中，PPO 需要三个模型：Actor, Reference, Reward. 它们的功能上文介绍过了。

但阅读相关文献，可以发现现在最常见的 PPO 是四个模型的：Actor, Critic, Reference, Reward. 多的一个 Critic 模型便是本章的重点。

5.1 原始版本的缺点

首先，在 RL 训练时有很多随机性：

  • 行为是随机的：对于一个 State，Actor 选择要做的 Action 是随机的。
  • 环境是随机的：对于一个 State，在 Actor 做出一个 Action 后，转换为新的 State，新 State 的选择可能是随机的。

这给训练带来了非常大的不稳定性，对于同样的初始状态，多个 Episode 得到的 Reward 值可能是截然不同的。另外，多个随机变量叠加起来，方差会成平方增长，导致 RL 的训练非常不稳定。

用一个例子来解释：

例如我们训练一个 Actor 躲避对手的攻击，躲避得越好 Reward 越高，同时对手的出招随机，普攻好躲、大招难逃。

此时，如果使用普通 PPO 进行训练，对于同一个 Actor，如果对手出普攻时会发现躲避得比较好，Reward 比较高，但对手出大招时总躲不掉，Reward 很低。这就给 RL 训练带来很大得麻烦，对于同一个躲避的操作，Reward 很不稳定方差很大。

为了解决这个问题，可以让随机的 Reward 都减掉一个基准值 Baseline，从而降低方差、稳定训练。这个 Baseline 的值便是 Critic 模型来决定的，下面进行说明。

5.2 引入 Critic 模型

Critic 模型也叫做 Value 函数 $V(s)$，它的作用是评估当前 Actor 在特定 State 情况下，可以得到的 Reward 的期望值。它的作用是评估在当前 State 条件下，该 Actor 能达到的平均水准。

继续沿用上面的例子：

  • 如果对手出大招 $s_1$ 时，$V(s_1)$ 就会比较低，代表这个 Actor 得分期望低
  • 如果对手出普攻 $s_2$ 时，$V(s_2)$ 就会比较高，代表这个 Actor 得分期望高。

那么我们将这个 Value 作为 Baseline，让 Reward 减去这个 Value: $R(s_t,a_t)-V(s_t)$. 就可以让不同随机情况下的奖励更加稳定。

继续沿用上面的例子：

  1. 如果对手出大招，Actor 躲避失败了：那么 $R(s_1,a)-V(s_1)$ 也不会过小，因为这个操作确实很困难，奖励时得补偿难度。
  2. 如果对手出普攻，Actor 躲避成功了：那么 $R(s_1,a)-V(s_1)$ 也不会很大，因为这个操作在期望之中，适当奖励即可。
  3. 如果对手出大招，Actor 躲避成功了：那么 $R(s_1,a)-V(s_1)$ 就会非常大，代表这个操作是超常发挥，得狠狠奖励。
  4. 如果对手出普攻，Actor 躲避失败了：那么 $R(s_1,a)-V(s_1)$ 就会非常小，因为这个操作是发挥失常，奖励值就是负数。

那么，对于同一个 Actor，最可能发生的事情就是 1 和 2，可以发现将 Reward 减去 Baseline 后，奖励值稳定多了，不会出现方差过大的情况。

综上，引入 Critic 后，PPO 总共需要四个模型：

  1. Actor：与环境交互的主体，基于当前环境观测到的 State 给出下一步 Action.
  2. Critic：评估 Actor 行为的教练，基于 Actor 在当前 State 的期望水准给出基准值。Critic 是和 Actor 一起训练的。
  3. Reward：给出最终分数的模型，基于环境规则给出 Reward. Reward 往往是预定义好的，因此参数冻结。
  4. Reference：参考模型，约束 PPO 训练不要让模型偏离原始模型过远，参数也是冻结的。
文章目录