机器学习 | 混合专家模型 (MoE)
混合专家模型 (Mixture of Experts, MoE):一种通过将多个“专家”子模型组合起来,通过路由模块动态选择部分专家处理不同输入,从而实现高效扩展参数规模、提升性能并降低计算成本的深度学习方法。
如果没有额外注明,本文的图片都来源于 A Review of Sparse Expert Models in Deep Learning,这是一篇挺不错的综述,对 MoE 研究的介绍挺全面。
0 结构 Structure
目前运用最广泛的 MoE 结构,是运用在 Transformer 的 FFN 层中的:FFN 层拆分为多个独立权重的专家,但 Attention 层并不会拆分为多个专家。另外,为了将 Token 分配给专家,还需要一个路由用来挑选专家。在 MoE 模型中,每个 Token 经过残差连接和归一化输入路由,路由选择一个(或多个)专家,Token 经过选择的专家 FFN 层后加权求和,输入下一个残差连接和归一化层。
MoE 模型和传统模型的结构对比如下,左侧为传统模型(稠密模型),右侧为 MoE 模型(稀疏模型)。
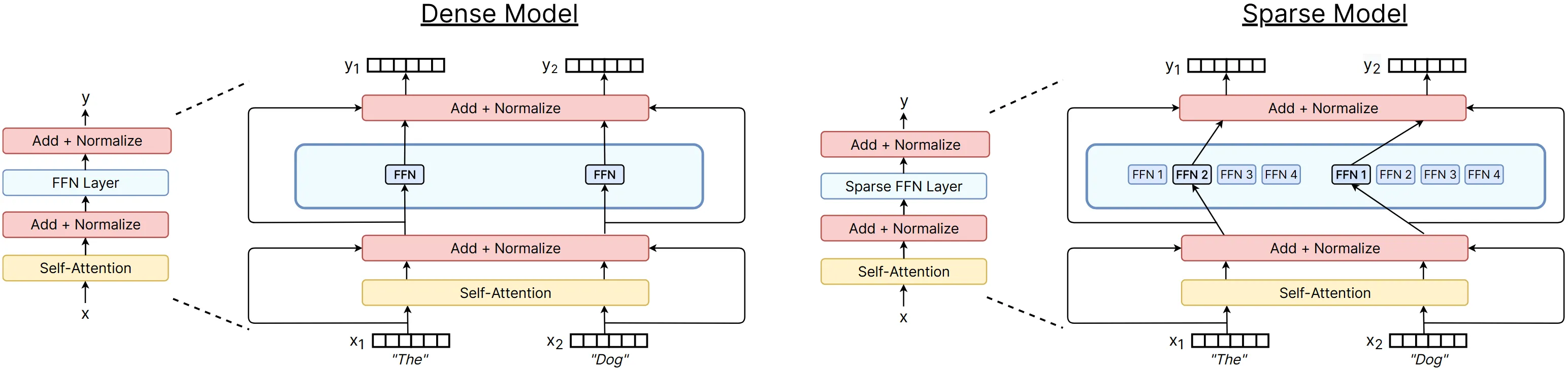
通过该结构,MoE 可以实现许多特性。首先是可以自由扩展参数规模,由于每次激活的专家较少,大部分专家参数是不纳入计算的,因此相对于传统模型,同参数量所需计算量大幅降低。其次是便于并行化,每个专家可以放在不同的计算设备上,该结构能自然地适配并行计算。最后最重要的是,相同参数量的 MoE 模型,模型能力往往较传统模型有明显提升。
从结构可以看出,MoE 中的重点无非分为三点,接下来会一一分析:
- 路由:怎么路由 Token?
- 专家:怎么配置专家数量和大小?
- 训练:怎么有效训练?
1 路由 Router
路由 Token 的方法非常多,这里挑选 3 个比较典型的方法,可以看 A Review of Sparse Expert Models in Deep Learning 深入了解。
1.1 哈希路由
原论文:Hash Layers For Large Sparse Models
哈希函数就可以作为一种简单的路由方式,通过哈希函数将每个 Token 通过映射到一个专家。这种方法的哈希函数在训练前挑选,路由方式直接静态确定,不包含可训练路由参数,也不参考任何语义信息。尽管这方案看起来过于简单粗暴,但仍然是一种有效的方案,甚至比下文会提到的 Switch Transformer 效果要好。
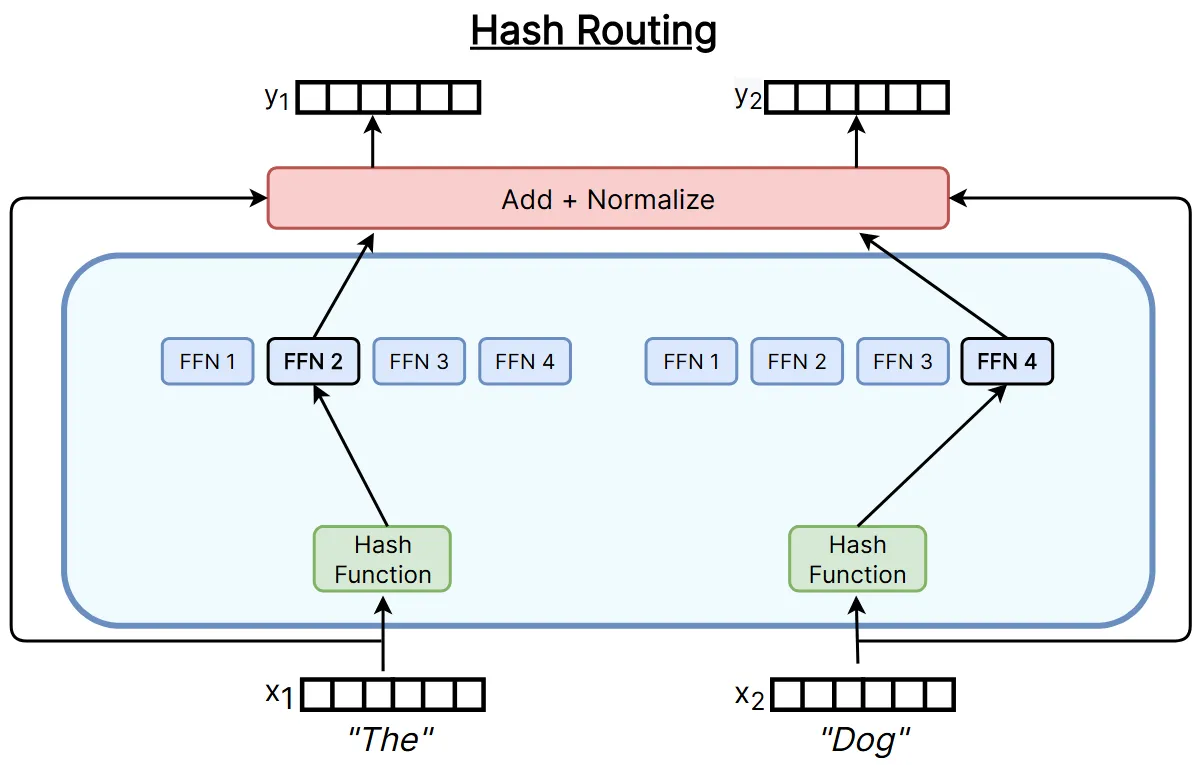
该方法最核心的就是哈希函数的挑选,有多种思路完成。下面介绍效果最好的两种哈希方法:
- 均衡随机哈希:初始化时,将词表中的 Token 按照出现频率分配给每个专家,构建查找表,同时确保每个专家负载均衡;运行时,当前 Token 通过查表映射给对应专家。
- 分散哈希:初始化时,对词表中的 Token 的 Embedding 进行 K-means 聚类,将每个类中的 Token 均匀分配给每个专家,构建查找表;运行时,当前 Token 通过查表映射给对应专家。
原文还提到了多重哈希的改进方案,限于篇幅不再展开。
1.2 Token 选专家的 Top-k 路由
原论文:
Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer
Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity
DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models
静态的哈希路由毕竟效果有限,要获得更好的效果,就需要可训练的动态路由方式了。Token 选专家的 Top-k 路由便是一种动态方法,本方法所代表的思想应该是目前最主流的。该方法的结构如下:
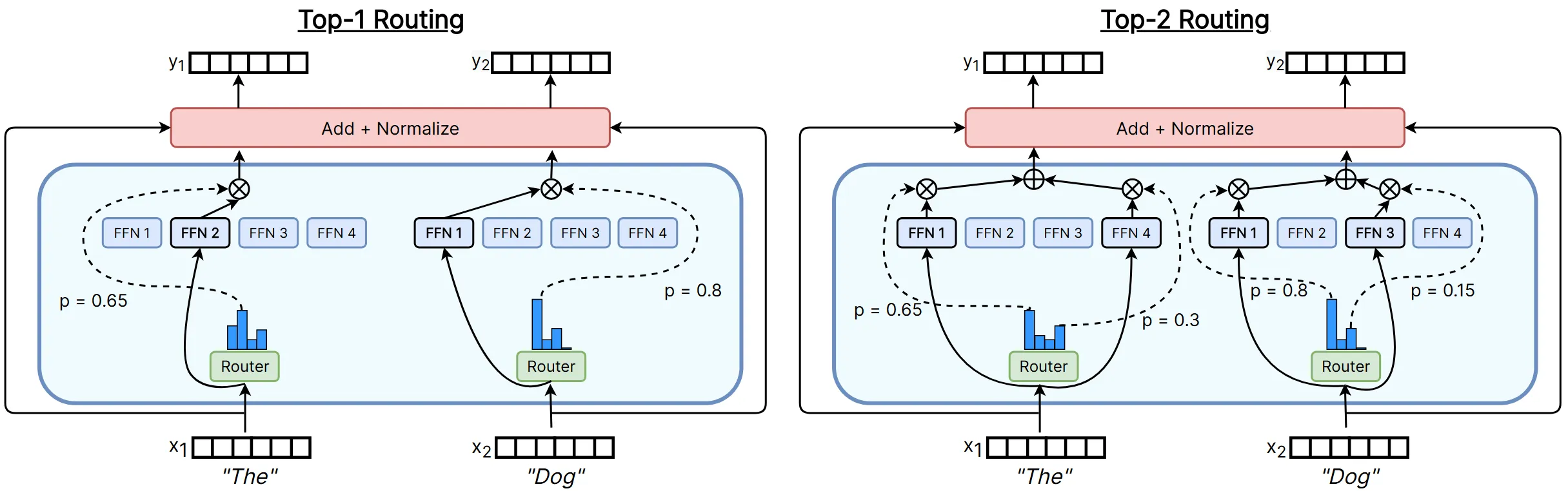
该方法的路由流程如下:
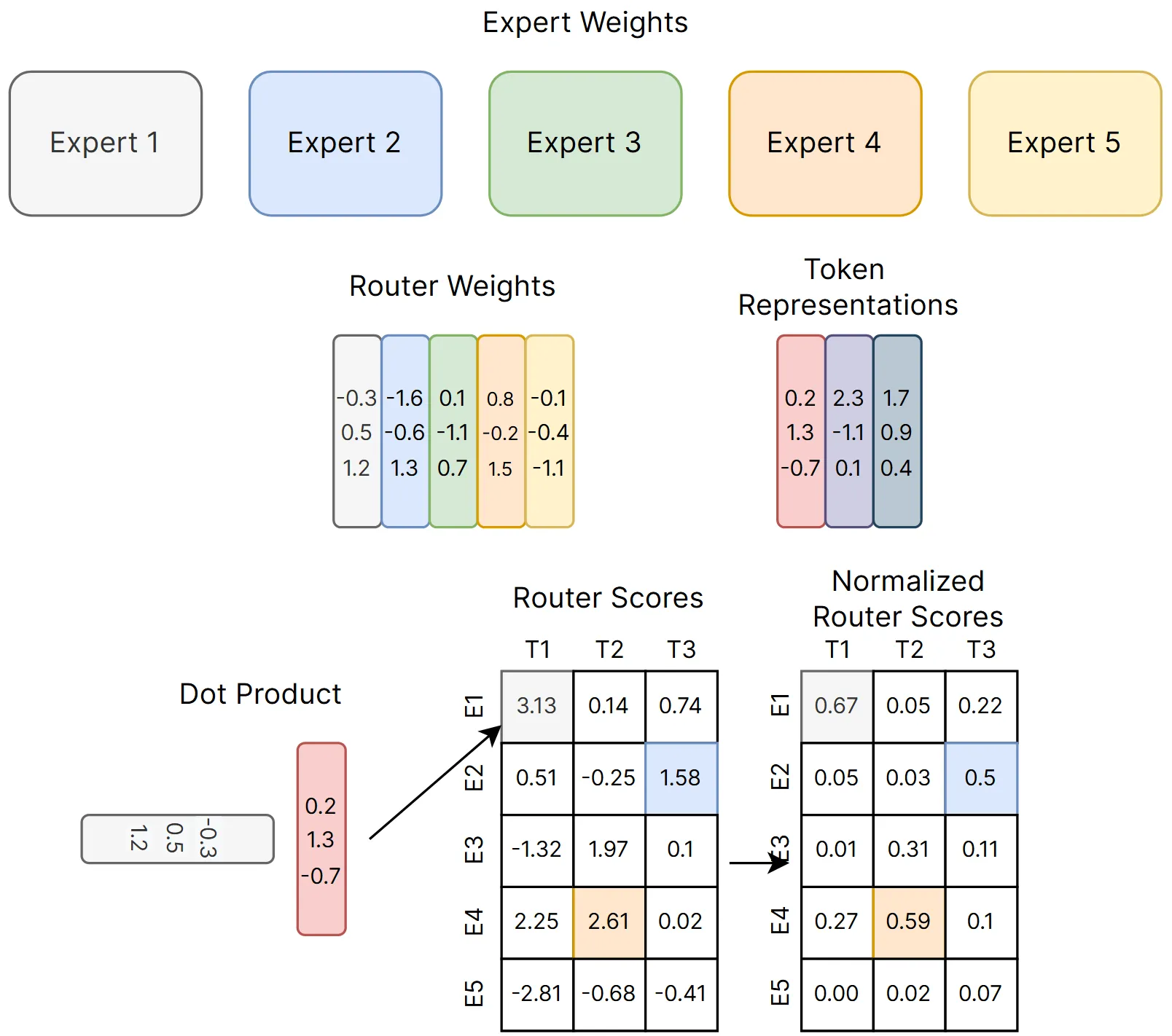
- 可训练的路由模块包含路由参数 $\boldsymbol{W}_g$,即下图中的 Router Weights。
- 要为 Token $x$ 选择专家,则与路由参数相乘 $H(x)=\boldsymbol{W}_g^{\text{T}}x$,即获得了下图中 Router Scores 中的一列。
- 接下来使用 Softmax 将每一列转为概率分布 $G(x)=\mathrm{Softmax}(H(x))$,即下图中 Normalized Router Scores 的一列。
- 最后,为 Token 选择概率值 Top-K 大的专家即可,图中 $k=1$。
- 选好专家后,再进行加权求和获得最后的结果 $y=\sum_{i=1}^{n}G(x)_i E_i(x)$。
用公式来表示:
$$ \begin{align} &y=\sum_{i=1}^{n}G(x)_i E_i(x)\\ &G(x)_i=\mathrm{KeepTopK}(\mathrm{Softmax}(x^{\text{T}}\boldsymbol{W}_g),k)_i\\ &\mathrm{KeepTopK}(v,k)_i= \begin{cases} v_i\quad\text{if}\;v_i\;\text{is in the top}\;k\;\text{elements of}\;v.\\ 0\;\quad\text{otherwise}. \end{cases} \end{align} $$
实际模型中将 Softmax 位置提到了 TopK 外侧,这样就能保证最后加权求和的权重和为 $1$,即:
$$ \begin{align} &y=\sum_{i=1}^{n}G(x)_i E_i(x)\\ &G(x)_i=\boxed{\mathrm{Softmax}}(\mathrm{KeepTopK}(x^{\text{T}}\boldsymbol{W}_g,k)_i)\\ &\mathrm{KeepTopK}(v,k)_i= \begin{cases} v_i\qquad\text{if}\;v_i\;\text{is in the top}\;k\;\text{elements of}\;v.\\ \boxed{-\infty}\quad\text{otherwise}. \end{cases} \end{align} $$
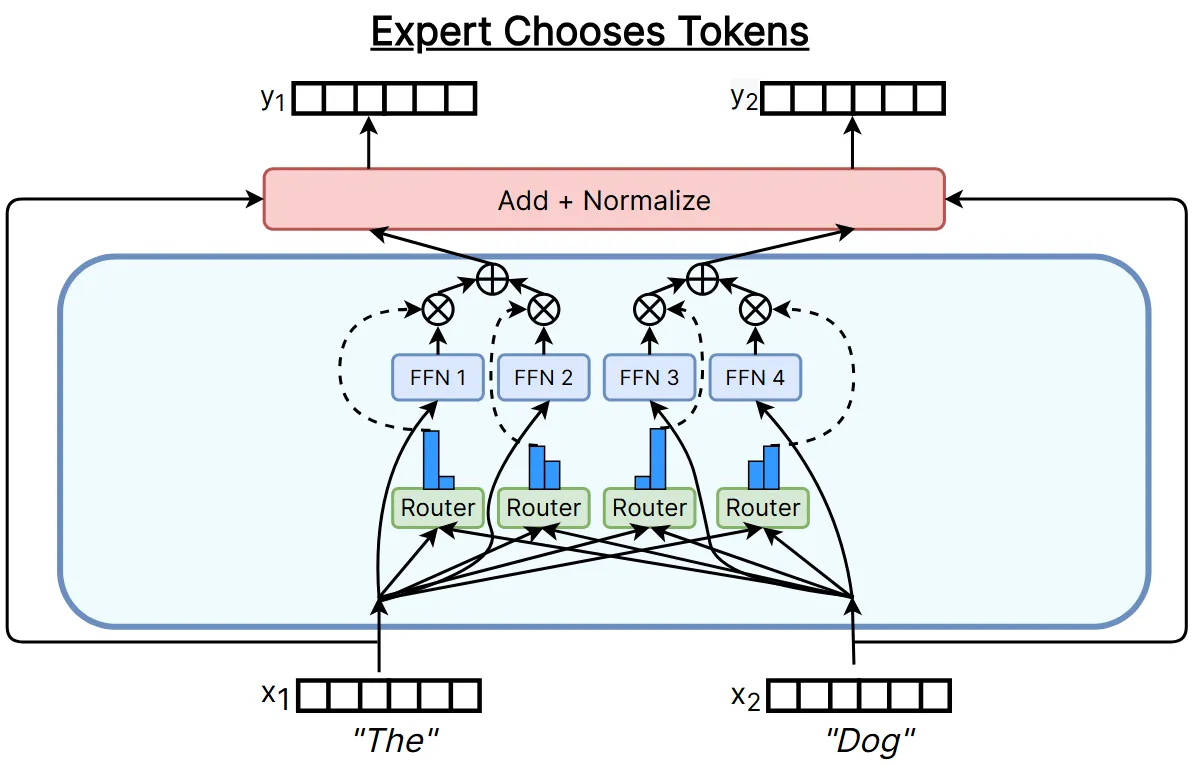
1.3 专家选 Token 的 Top-k 路由
原论文:Mixture-of-Experts with Expert Choice Routing
上一节 1.2 中提到的方法可以理解为每个 Token 在专家组中挑选专家,而本节 1.3 提到的方法正好相反,是每个专家在 Token 序列中挑选 Token。
这两种方法实际上差距不大,可以用下图来理解:左侧为 Token 选专家,对每一列进行 Softmax 后取 Top-K,将 Token 分配给对应专家;右侧为专家选 Token,对每一行进行 Softmax 后取 Top-K,将专家分配给 Token。
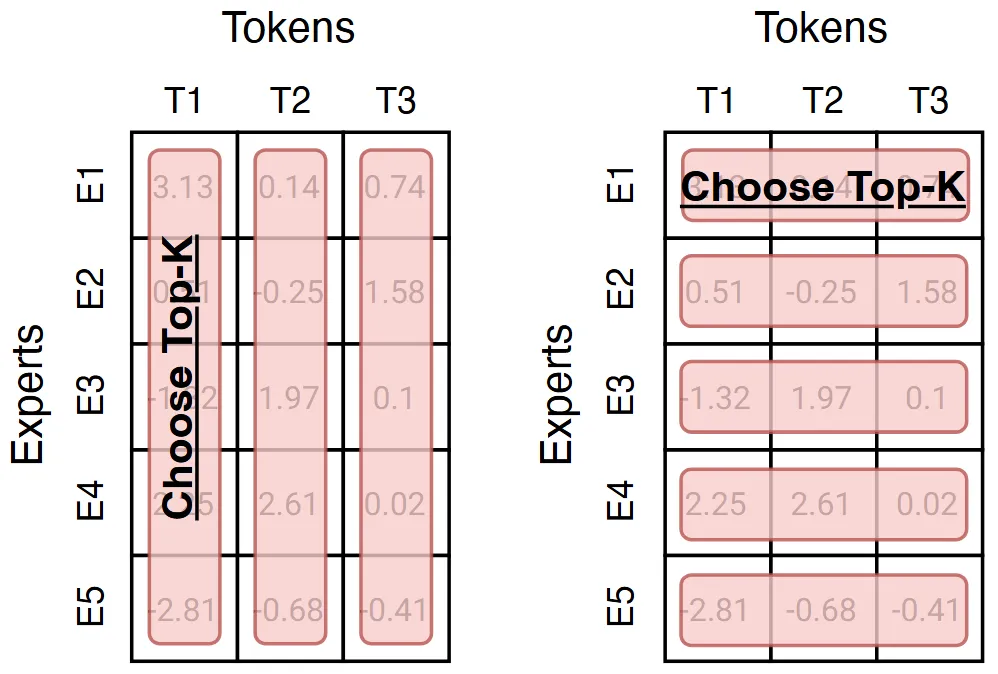
容易发现,该方法存在一个问题:有些令牌可能不会发送给任何专家(所有专家都没选),或者有些令牌可能会发送给所有专家(所有专家都选了)。但实际上该问题的影响并不大,并且可以视作模型在自动进行算力分配,为更重要的 Token 分配更多的专家提供计算,实现了算力自适应。
除此之外,该方法每个专家都会选择 $K$ 个 Token,天然地完成了专家间的负载均衡,训练时无需担心有专家获得的训练 Token 数量不足。
2 专家 Experts
在早期 MoE 的做法是保持模型 FFN 的大小,每个 FFN 专家都是全尺寸的。而目前的主流做法是减小模型 FFN 的大小,相当于把原始 FFN 切成多份,每份参数量都较小。这种方法能够起到节省算力的作用,并且更多小专家效果实际上比一个大专家效果更好。
除此之外,DeepSeek 团队还进行了进一步创新,提出了共享专家和路由专家的概念:共享专家是每个 Token 必选的专家,路由专家是由路由模块额外给 Token 选择的专家。该方法的思想是有些特征是每个 Token 均共有的,因此分配共享专家专用于处理这些共有特征,而路由专家则专注于每个 Token 中独特的特征。
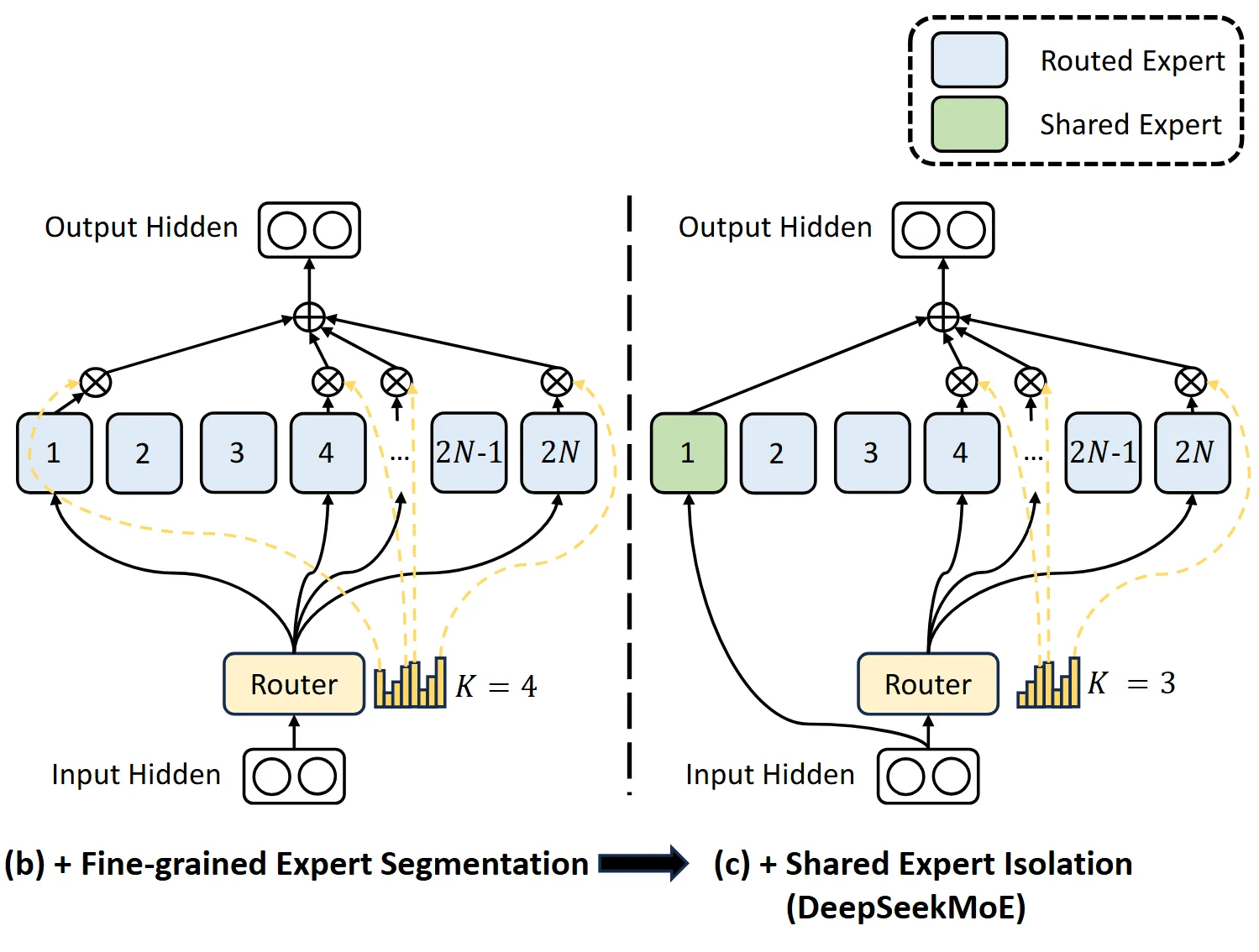
图片来源:DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models
下面的表格收录了一些有代表性的模型对专家数量和大小的配置,其中 Routed 代表总专家数,Active 代表路由专家数,Shared 代表共享专家数,Fine-grained ratio 代表每一个专家参数量大小相对于传统模型的比例,即切分大小。
观察可以发现,大多数模型都保持着 $(\text{Active}+\text{Shared})\times\text{FineGrainedRatio}\approx1$,即实际运行消耗的算力和传统模型相当,但所有模型的 $\text{Routed}\times\text{FineGrainedRatio}\gg1$,即模型总参数量实际上是远大于传统模型的。可以看出,目前主流模型的做法是使用更多专家学习更多的知识总量,实际运行时只激活少许专家,保证算力消耗和传统模型相当。
| Model | Routed | Active | Shared | Fine-grained ratio |
|---|---|---|---|---|
| GShard | 2048 | 2 | 0 | |
| Switch Transformer | 64 | 1 | 0 | |
| ST-MOE | 64 | 2 | 0 | |
| Mixtral | 8 | 2 | 0 | |
| DBRX | 16 | 4 | 0 | |
| Grok | 8 | 2 | 0 | |
| DeepSeek v1 | 64 | 6 | 2 | 1/4 |
| Qwen 1.5 | 60 | 4 | 4 | 1/8 |
| DeepSeek v3 | 256 | 8 | 1 | 1/14 |
| OlMoE | 64 | 8 | 0 | 1/8 |
| MiniMax | 32 | 2 | 0 | ~1/4 |
| Llama 4 (maverick) | 128 | 1 | 1 | 1/2 |
来源:Stanford CS336 Lecture 4 Course Materials
3 训练 Training
MoE 模型训练时非常重要的是不同专家间的训练平衡,如果没有确保每个专家均衡训练,很有可能模型收敛到使用唯一专家处理所有 Token,让 MoE 模型绝大多数参数直接报废,行为退化为一个传统模型。
3.1~3.3 介绍的都是用于平衡专家训练的方法,3.4 介绍的是稳定训练的一种方式。
3.1 Noisy Top-K Gating
原论文:Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer
噪声 Top-K 门控方式向原始 Top-K 方法(1.2 节)中引入了随机的噪声扰动,使 Token 选择专家时不再稳定地选择到理论 Top-K,而有可能探索到其他次优的专家。尽管噪声扰动会降低效率,但是该方法能够均衡每个专家的训练,探索更多可能性,从而增强模型鲁棒性,总体是值得的。
该方法的公式如下,其中 $\epsilon \sim \mathcal{N}(0, 1)$.
$$ \begin{align} &y=\sum_{i=1}^{n}G(x)_i E_i(x)\\ &G(x)_i=\mathrm{Softmax}(\mathrm{KeepTopK}(H(x),k)_i)\\ &H(x)_i=x^{\text{T}}\boldsymbol{W}_g+\epsilon\cdot\log\left(1+e^{(x\cdot W_{noise})_i}\right)\\ &\mathrm{KeepTopK}(v,k)_i= \begin{cases} v_i\qquad\text{if}\;v_i\;\text{is in the top}\;k\;\text{elements of}\;v.\\ -\infty\quad\text{otherwise}. \end{cases}\\ \end{align} $$
可以看到,$H(x)$ 项加入了噪声扰动,它进行 $\mathrm{KeepTopK}$ 操作得到的结果很可能和原始的不同,让模型训练时能够探索到更全面的专家。
3.2 Differentiable Load Balancing Loss
原论文:Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity
该方法是对 3.1 中方法的简化,核心思想是通过添加一个在均匀路由条件下取到最小值的损失值,引导模型训练时均衡负载。
对于 $N$ 个专家和包含 $T$ 个 Token 的批次 $\mathcal{B}$,损失值的计算方式如下:
$$ \mathrm{loss}=\alpha\cdot N\cdot\sum_{i=1}^{N}f_i\cdot P_i $$
其中,$f_i$ 是该批次中,分配给专家 $i$ 的 Token 比例(可理解为实际分配比例):
$$ f_i=\frac{1}{T}\sum_{t\in\mathcal{B}}\mathbb{1}(\text{Token}\;t\;\text{selects Expert}\;i) $$
$P_i$ 是该批次中,给专家 $i$ 分配 Token 的概率比例(可理解为预计分配比例):
$$ P_i=\frac{1}{T}\sum_{t\in\mathcal{B}}p_i(t) $$
参数 $\alpha$ 是控制该损失值力度的超参数,原论文中取 $\alpha=10^{-2}$.
可以发现,理想情况下当模型负载均衡时,$f_i$ 和 $P_i$ 均取到 $1/N$,此时损失之能取到最小值 $\mathrm{loss}=\alpha$,该方法就是通过这种损失值设计促进负载均衡的。最后,该方法的可微性由 $P_i$ 提供,但 $f_i$ 是不可微的。
原论文提出的方法用于平衡专家间的训练负载,但实际上该方法非常灵活,例如若将 $f_i$ 和 $P_i$ 改为分配给设备(比如 GPU)的 Token 比例,那么该方法就可以完成训练时多个设备的负载均衡。
3.3 Auxiliary-Loss-Free Load Balancing
原论文:DeepSeek-V3 Technical Report
该方法提供了一种无需辅助损失值的负载均衡方式,负载均衡参数和模型参数的训练分离,避免负载均衡参数对模型参数造成干扰。
$$ g_{i,t}'= \begin{cases} s_{i,t}\quad \text{if}\;s_{i,t}+b_i\in\mathrm{TopK}(\{s_{i,t}+b_i\mid1\leq j\leq N_r\},K_r).\\ 0\;\:\:\quad\text{otherwise}. \end{cases} $$
每个训练步后,若专家 $i$ 获得了过多训练 Token(过载),那么通过参数 $\gamma$ 降低 $b_i$,使该专家后续获得的 Token 数目减小;若专家 $i$ 获得的训练 Token 不足(欠载),那么通过参数 $\gamma$ 提升 $b_i$,使该专家后续获得的 Token 数目增大。
可以发现,该方法的 $b_i$ 项仅作用于取 $\mathrm{TopK}$ 的过程中,不作用于结果,因此不影响模型参数的训练。
3.4 Z-Loss
为了节约显存开销,大模型训练时采用 bf16 进行计算,该数据类型能够表达的数值范围有限,如果数值过大或者过小很有可能导致溢出,最终导致训练不稳定。换用 fp32 当然能解决这个问题,但双倍显存占用还是代价太大,因此提出了 Z-Loss 辅助损失值,用于控制 Logits 值的大小
Z-Loss 的公式如下:
$$ L_z(x)=\frac{1}{B}\sum_{i=1}^{B}\left(\log\sum_{j=1}^{N}e^{x_j^{(i)}}\right)^2 $$
其中,$B$ 代表当前批次大小,$N$ 为专家数量,$x$ 为路由模块的专家 logits 输出。
这个损失值的意思是,将每个专家的 logits 输出取指数求和,再取对数,接着在整个批次 $B$ 上求平均,得到最后的结果。该损失值相当于惩罚过大的 logits 输出,防止路由模块输出过大 logits 值使 Softmax 过程溢出,确保模型训练的稳定性。
本文采用 CC BY-SA 4.0 许可,本文 Markdown 源码:Haotian-BiJi