组相关策略优化 (Group Relative Policy Optimization, GRPO)：强化学习中的一种策略优化方法，通过采样求期望节省了 PPO 中的 Value (Critic) 模型。Deepseek-R1 的训练方法。

• DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models
• DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning

1 回顾 PPO

在 PPO 中，我们需要四个模型：

1. Policy (Actor) Model
2. Value (Critic) Model
3. Reference Model
4. Reward Model

其中，参数更新的是 Policy 和 Value 模型，Reference 和 Reward 的参数是不训练的。另外，通常这 4 个模型都是相同参数规模的，也就是说我们需要目标模型四倍大小的显存来进行训练，显存和算力消耗很大。

为了降低开销，涌现出了不少策略优化算法，针对的就是怎么省去这四个模型中的其中一个模型。例如之前的笔记中，DPO 省掉了 Value 模型同时是 Off-Policy 算法，SimPO 省掉了 Value 和 Reference 模型。

而本篇笔记分享的 GRPO 方法，就是通过采样求期望节省了 PPO 中的 Value 模型，只需要加载三个模型。

2 GRPO 的差异点

要省掉 PPO 中的 Value 模型，首先得看看这个模型做了什么，有什么方法去近似它所做的工作。Value 模型的作用是评估当前 Policy 在特定 State 情况下，可以得到的 Reward 的期望值。最终基于 Value 模型给出的值，让奖励值更稳定，方差减小，从而让 RL 训练更稳定。

看到这个期望值，我们容易想到，期望可以用采样求均值的方法来近似。采样 Policy 这个过程不需要引入额外的模型，因此通过采样求均值是可以省掉 Value 模型的。这便是 GRPO 朴素简单的思想。

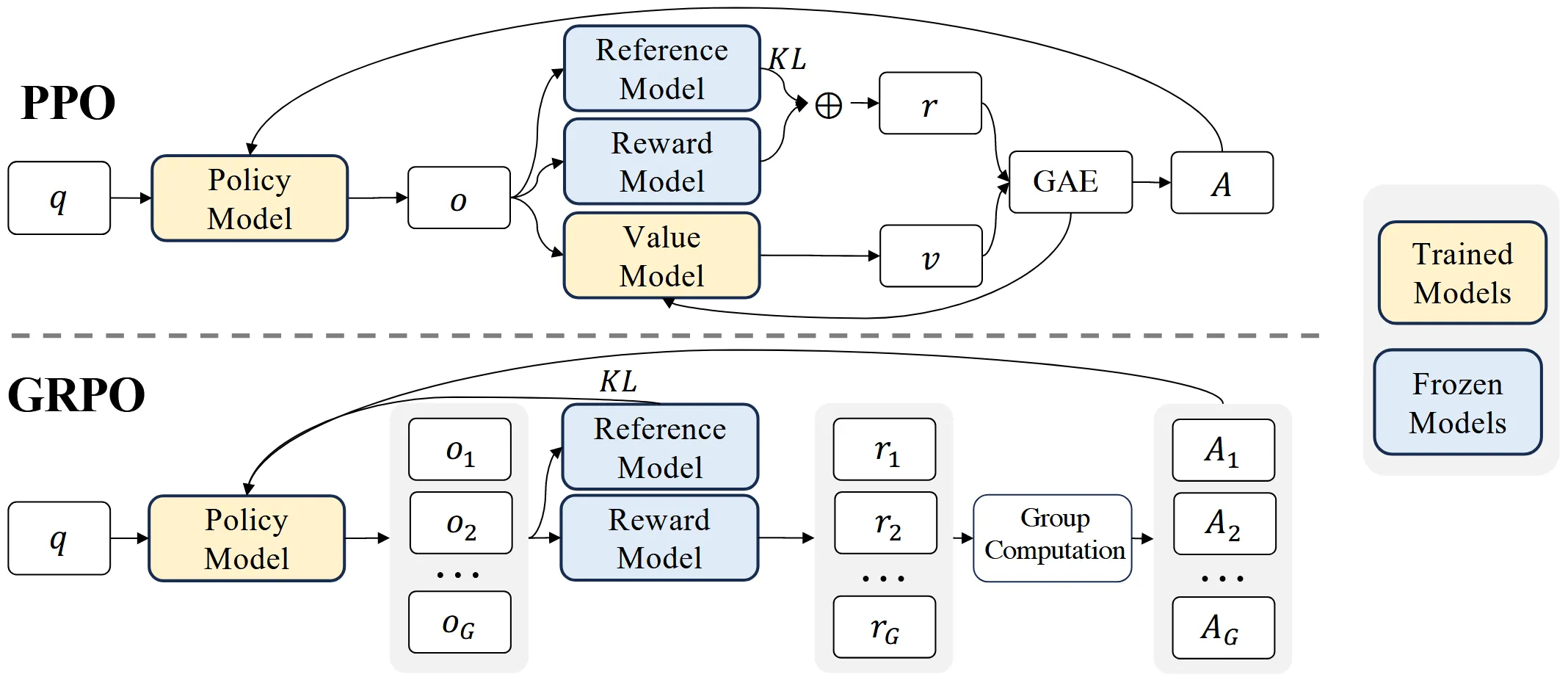
接下来，根据上图对比一下 PPO 和 GRPO 的差异。

首先最明显的就是上文说过的省去了 Value 模型，可以看到 GRPO 一次采样了 $G$ 个输出 $o_1,o_2,\dots ,o_G$. 对于这 $G$ 个输出，通过 Reward 模型获得每个输出的奖励值 $r_1,r_2,\dots ,r_G$. 然后通过计算这 $G$ 个采样的均值和方差，获得最终的优势值 $A_1,A_2,\dots ,A_G$. 然后基于优势值来指导模型更新。

除此之外，还能注意到，$\text{KL}$ 惩罚的施加位置不同。PPO 的 $\text{KL}$ 惩罚是逐 Token 计算的，而 GRPO 的 $\text{KL}$ 惩罚是直接拿 Policy 和 Reference 算出来施加到最终奖励值的。

3 GRPO 的细节

GRPO 的目标函数是：

$$\begin{array}{rl}& \underset{\theta }{max}\mathbb{E}[(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }},\{o_i{\}}_{i=1}^G\sim {\pi }^{\prime }(a_t|s_t)]\\ & \frac{1}{G}\sum _{i=1}^G[min(\frac{p_{\theta }(a_t\mid s_t)}{p_{{\theta }^{\prime }}(a_t\mid s_t)}{A}_i,\mathrm{clip}(\frac{p_{\theta }(a_t\mid s_t)}{p_{{\theta }^{\prime }}(a_t\mid s_t)},1-ϵ,1+ϵ)A_i)-\beta {\mathbb{D}}_{KL}({\pi }_{\theta }\Vert {\pi }_{\mathrm{ref}})]\end{array}$$

其中：

$$\begin{array}{rl}{\mathbb{D}}_{KL}({\pi }_{\theta }\Vert {\pi }_{\mathrm{ref}})& =\frac{{\pi }_{\mathrm{ref}}(a_t\mid s_t)}{{\pi }_{\theta }(a_t\mid s_t)}-\log \frac{{\pi }_{\mathrm{ref}}(a_t\mid s_t)}{{\pi }_{\theta }(a_t\mid s_t)}-1\\ A_i& =\stackrel{\sim }{r_i}=\frac{r_i-\mathrm{mean}(\{r_1,r_2,\cdots ,r_G\})}{\mathrm{std}(\{r_1,r_2,\cdots ,r_G\})}\end{array}$$

可以看到，GRPO 的目标函数和 PPO 的结构几乎一致，重要区别就是 $A_i$ 的计算方式是将 $G$ 个采样的奖励值 $\{r_1,r_2,\cdots ,r_G\}$ 归一化。

另外，还需要注意 GRPO 估计 $\text{KL}$ 惩罚时，使用了一种无偏的蒙特卡洛方法：http://joschu.net/blog/kl-approx.html