题目 | 方格取数 - 颢天笔记

AcWing 1027. 方格取数

动态规划典型例题

https://www.acwing.com/problem/content/1029/

题目

设有 $N\times N$ 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字 $0$。如下图所示：

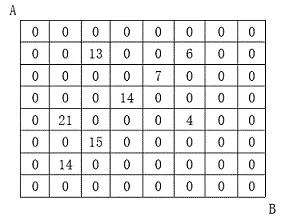
某人从图中的左上角 $A$ 出发，可以向下行走，也可以向右行走，直到到达右下角的 $B$ 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 $0$）。

此人从 $A$ 点到 $B$ 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式

第一行为一个整数 $N$，表示 $N\times N$ 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

行和列编号从 $1$ 开始。

一行 “0 0 0” 表示结束。

输出格式

输出一个整数，表示两条路径上取得的最大的和。

数据范围

$N\leq 10$

输入样例

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

输出样例

67

题解

能否分为两次取数？

一次取数的问题很好解决，该题的难点是进行了两次取数。需要注意的一点是，不可将两次取数分别处理，因为两次分别的最优操作在总体上并不一定是最优操作。如果这点无法理解，可以参考以下示例：

$$ \begin{matrix} 0 & 100 & 100 & 1 & 0\\ 0 & 1 & 100 & 100 & 0\\ 0 & 0 & 1 & 100 & 0\\ 0 & 0 & 0 & 100 & 0\\ 0 & 0 & 0 & 0 & 0 \end{matrix} $$

如果我们将其分为两次取数来思考，第一次取数时，最优策略如下，一共取到了 $600$：

$$ \begin{matrix} \framebox{0} & \framebox{100} & \framebox{100} & 1 & 0\\ 0 & 1 & \framebox{100} & \framebox{100} & 0\\ 0 & 0 & 1 & \framebox{100} & 0\\ 0 & 0 & 0 & \framebox{100} & \framebox{0}\\ 0 & 0 & 0 & 0 & \framebox{0} \end{matrix} $$

第二次取数时，最优策略如下，一共取到了 $2$：

$$ \begin{matrix} \framebox{0} & \framebox{0} & 0 & 1 & 0\\ 0 & \framebox{1} & \framebox{0} & 0 & 0\\ 0 & 0 & \framebox{1} & \framebox{0} & \framebox{0}\\ 0 & 0 & 0 & 0 & \framebox{0}\\ 0 & 0 & 0 & 0 & \framebox{0} \end{matrix} $$

但是我们通过目测都能发现更优的取法（方框代表第一次取，圆括号代表第二次取），一共能取 $603$：

$$ \begin{matrix} \framebox{(0)} & \framebox{100} & \framebox{100} & \framebox{1} & 0\\ (0) & (1) & (100) & \framebox{100} & 0\\ 0 & 0 & (1) & \framebox{100} & 0\\ 0 & 0 & (0) & \framebox{100} & \framebox{0}\\ 0 & 0 & (0) & (0) & \framebox{(0)} \end{matrix} $$

这就是为什么两次最优不等于总体最优。

朴素解法

先考虑仅一次操作的情形，$dp(i,j)=\max\left\{dp(i-1,j),dp(i,j-1)\right\}+mat(i,j)$，其中 $dp(i,j):=$ 从 $(1,1)$ 走到 $(i,j)$ 能取到的数字的和的最大值。

我们从一次操作再推广到两次，令 $dp(i,j,k,l):=$ 两次取数分别为从 $(1,1),(1,1)$ 走到 $(i,j),(k,l)$ 的情况能取到的数字的和的最大值。

此时，转移方式有四种，来源分别为：

第一次向下，第二次向下：$dp(i-1,j,k-1,l)$
第一次向右，第二次向下：$dp(i,j-1,k-1,l)$
第一次向下，第二次向右：$dp(i-1,j,k,l-1)$
第一次向右，第二次向右：$dp(i,j-1,k,l-1)$

转移后，我们需要加上本次取得数，此时就得考虑重复取数的情况：我们不能将一个数取两次

解决方法很简单，如果两次取的数相同，则只加一次，若不同，则加上取得两个不同的数：

若 $i=k$ 且 $j=l$：$mat(i,j)$
反之：$mat(i,j)+mat(k,l)$

综上，转移方式即为：

$$ \begin{align} dp(i,j,k,l)=&max\{\\ &dp(i,j,k,l),\\ &dp(i-1,j,k-1,l)+t,\\ &dp(i,j-1,k-1,l)+t,\\ &dp(i-1,j,k,l-1)+t,\\ &dp(i,j-1,k,l-1)+t\\ &\} \end{align} $$

其中：

$$ t= \begin{cases} mat(i,j), i=k\;且\;j=l\\ mat(i,j)+mat(k,l), 其他 \end{cases} $$

遍历所有 $i,j,k,l$ 后，答案即为 $dp(N,N,N,N)$

时间复杂度：$O(N^4)$
空间复杂度：$O(N^4)$

#include <bits/stdc++.h>
#define endl '\n'

using namespace std;

const int MAXN = 15;
int mat[MAXN][MAXN];
int dp[MAXN][MAXN][MAXN][MAXN];

void solve()
{
    int N;
    cin >> N;
    int a, b, c;
    while (cin >> a >> b >> c, a || b || c)
        mat[a][b] = c;
    for (int i = 1; i <= N; i++)
    {
        for (int j = 1; j <= N; j++)
        {
            for (int k = 1; k <= N; k++)
            {
                for (int l = 1; l <= N; l++)
                {
                    int t = mat[i][j];
                    if (i != k || j != l)
                        t += mat[k][l];
                    dp[i][j][k][l] = max({dp[i][j][k][l],
                                          dp[i - 1][j][k - 1][l] + t,
                                          dp[i - 1][j][k][l - 1] + t,
                                          dp[i][j - 1][k - 1][l] + t,
                                          dp[i][j - 1][k][l - 1] + t});
                }
            }
        }
    }
    cout << dp[N][N][N][N] << endl;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    solve();
    return 0;
}

优化维数

我们让两次取数同时进行，即两次取数的路径长一致，令路径长度为 $s$. 此处为了编程方便，点 $(x,y)$ 路径长度的含义为 $x+y$ 而非 $x+y-2$.

那么，记 $dp(s,i,k):=$ 两次取数分别为从 $(1,1),(1,1)$ 走到 $(i,s-i),(k,s-k)$ 的情况能取到的数字的和的最大值。

我们发现，之前四维才能表示的情况，现在用三维就能表示出现了，由此就省下了一个维度的复杂度。算法的其他部分一致。

时间复杂度：$O(N^3)$
空间复杂度：$O(N^3)$

#include <bits/stdc++.h>
#define endl '\n'

using namespace std;

const int MAXN = 15;
int mat[MAXN][MAXN];
int dp[2 * MAXN][MAXN][MAXN];

void solve()
{
    int N;
    cin >> N;
    int a, b, c;
    while (cin >> a >> b >> c, a || b || c)
        mat[a][b] = c;
    for (int s = 2; s <= 2 * N; s++)
    {
        for (int i = 1; i < s; i++)
        {
            for (int k = 1; k < s; k++)
            {
                int j = s - i, l = s - k;
                int t = mat[i][j];
                if (i != k || j != l)
                    t += mat[k][l];
                dp[s][i][k] = max({dp[s][i][k],
                                   dp[s - 1][i - 1][k - 1] + t,
                                   dp[s - 1][i - 1][k] + t,
                                   dp[s - 1][i][k - 1] + t,
                                   dp[s - 1][i][k] + t});
            }
        }
    }
    cout << dp[2 * N][N][N] << endl;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    solve();
    return 0;
}

题目 | 方格取数

题目