数据结构 | 并查集、种类并查集
维护例如“亲戚的亲戚是亲戚”这种关系的数据结构:并查集 (DST, Disjoint Set Union)
维护例如“敌人的敌人是朋友”这种关系的数据结构:种类并查集
1 并查集
1.1 分析
并查集通常使用数组来实现,例如我们有 0、1、2、3、4 五个元素,用 int father[5] 来存储,该数组的下标为数组元素,值为父节点(下文会解释)。
初始化时,令 father[i] = i,即 father[0] = 0, father[1] = 1, father[2] = 2, father[3] = 3, father[4] = 4.
此时代表着,这五个元素自成一派,一共有五类元素。用以下图来表示:
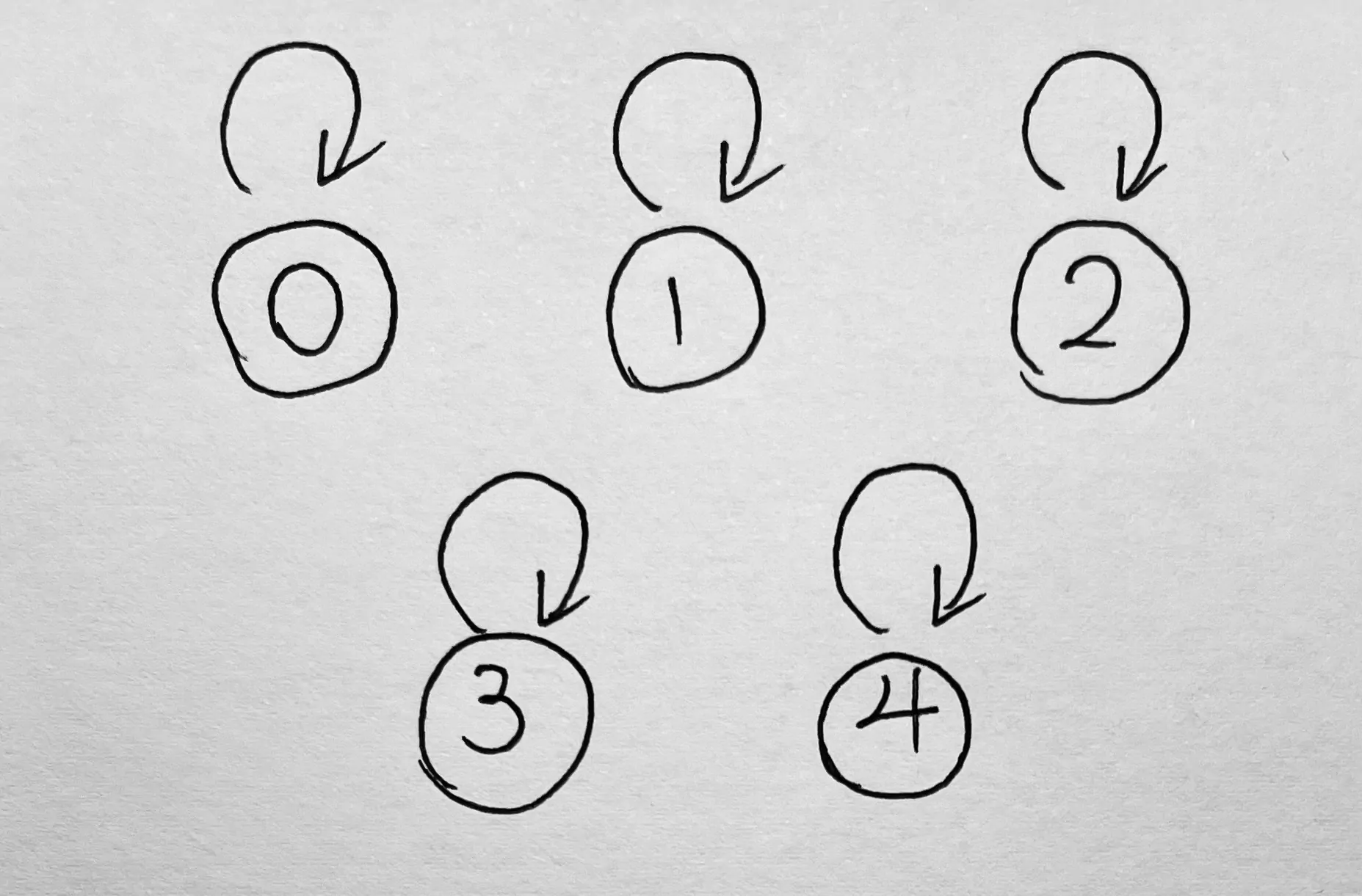
如果我们要将 0、1 分为一类,2、3、4 分为另一类,那么我们需要这样设置:father[1] = 0, father[3] = 2, father[4] = 2,此时我们称 1 的父节点是 0,3、4 的父节点是 2。此时 0 和 2 为根节点,我们将父节点为自身的节点叫根节点,从下图可以形象地理解。
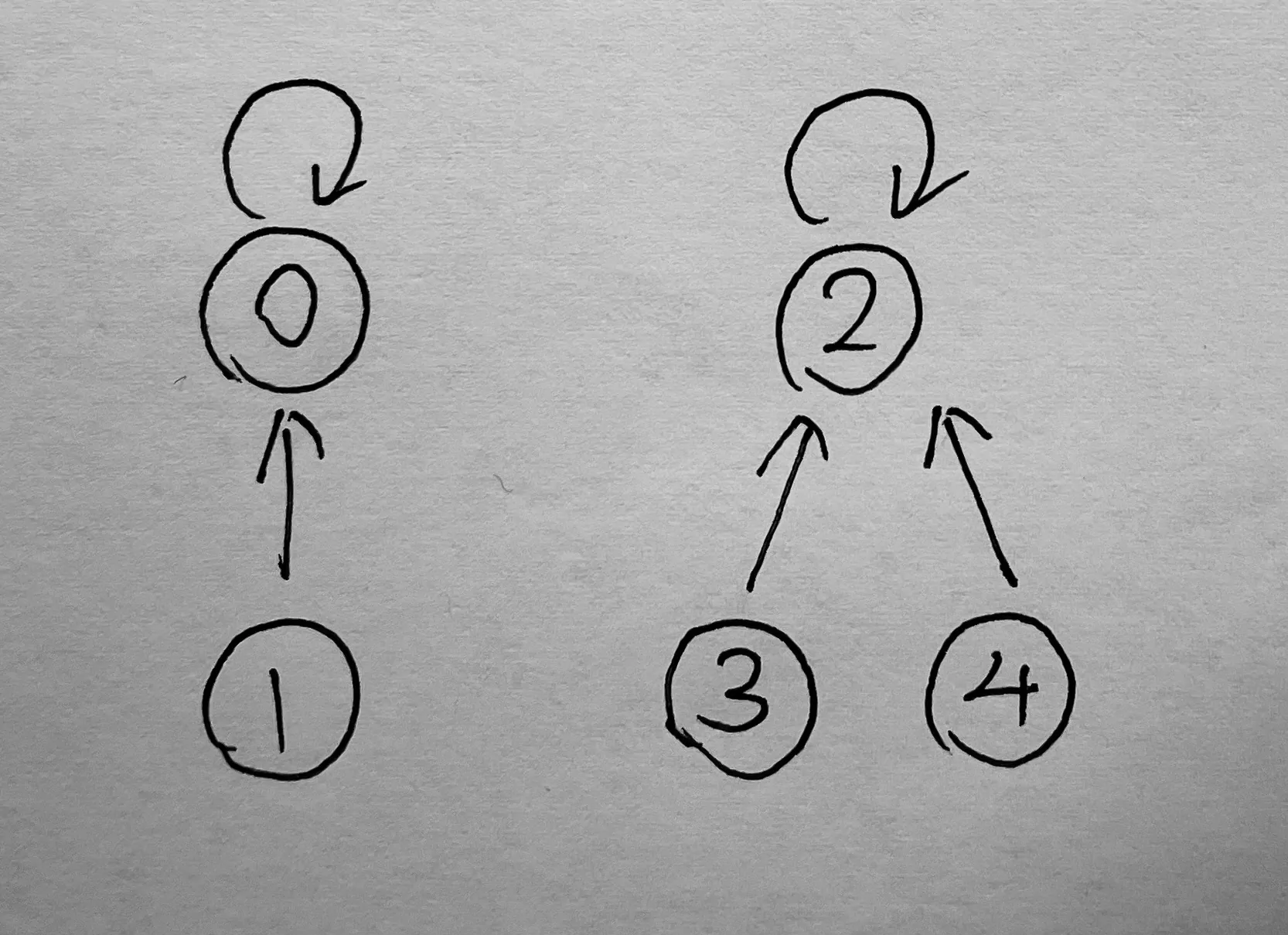
如果我们要把这两类合成一类呢,可以直接设置:father[2] = 0,即将一类的根节点指向另一类的根节点。
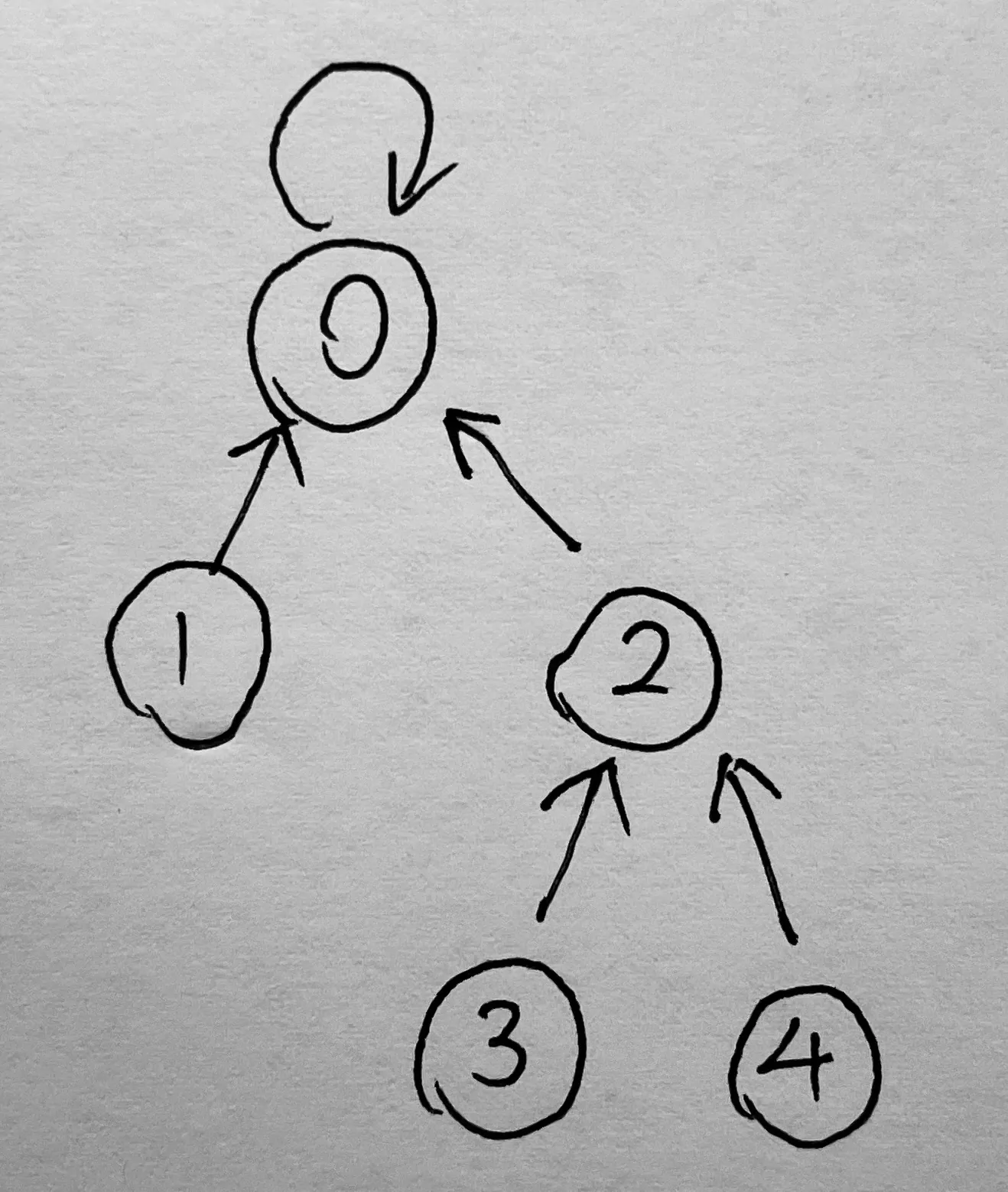
上面,已经讲了并查集的初始化和合并操作,并查集还剩下一种操作,就是查询。我们可以查询两个元素的根节点是否相同,如果相同那么我们就能判断这两个元素属于一类,反正不属于一类。
查询操作使用递归,我们查询该节点的父节点,再查询父节点的父节点直到根节点。以上图 9 为例:
- father[4] != 4 可知 4 不是根节点
- father[4] == 2 可知 4 的父节点是 2
- father[2] != 2 可知 2 不是根节点
- father[2] == 0 可知 2 的父节点是 0
- father[0] == 0 可知 0 就是根节点,查询完成,得到 4 的根节点为 0.
1.2 朴素实现
// 朴素版并查集(不推荐使用)
int fa[MAXN];
void init(int n)
{
for (int i = 1; i <= n; i++)
fa[i] = i;
}
int find(int x)
{
if(fa[x] == x)
return x;
else
return find(fa[x]);
}
void merge(int i, int j)
{
fa[find(i)] = find(j);
}1.3 可优化项目
1.3.1 路径压缩
在并查集中,合并元素常常会使树的深度越来越大,而我们的查询操作是采用递归,层层向上查询。如果元素的深度太大,那么我们的查询效率会很低,因此我们需要优化元素的排布。
因为进行该优化得查询根节点,我们不妨就将它与查询操作合并到一起,这样我们每次查询就顺带优化了该并查集。如下图:
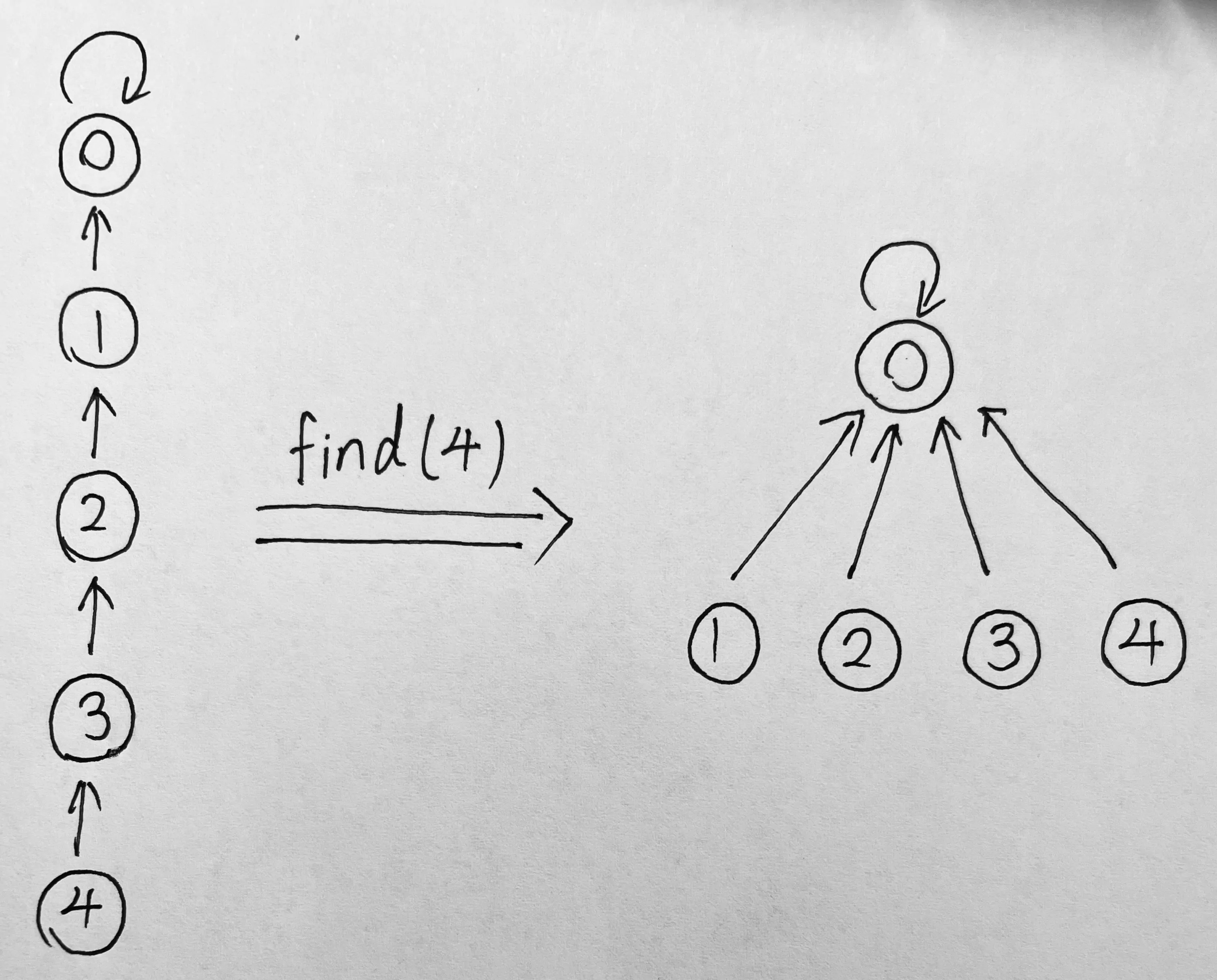
// 路径压缩版并查集(最常使用)
int fa[MAXN];
void init(int n)
{
for (int i = 1; i <= n; i++)
fa[i] = i;
}
int find(int x)
{
return x == fa[x] ? x : (fa[x] = find(fa[x])); // 注1
}
void merge(int i, int j)
{
fa[find(i)] = find(j);
}注1:
在 C 语言中,三元运算符 ? : 的优先级比赋值运算符 = 高,因此如果不加括号写成 x == fa[x] ? x : fa[x] = find(fa[x]),编译器会识别为 (x == fa[x] ? x : fa[x]) = find(fa[x]) 导致编译失败。
在 C++ 中,三元运算符 ? : 的优先级与赋值运算符 = 相同,从右至左结合,因此不加括号编译器也会正确识别为 x == fa[x] ? x : (fa[x] = find(fa[x])),但为了代码可读性和泛用性,建议加上括号。
参考资料:https://en.cppreference.com/w/cpp/language/operator_precedence#:~:text=In%20C%2C%20the,page%20for%20details.
1.3.2 启发式合并(按秩)
理想状况下,经过路径压缩操作,整个并查集应该为一个深度为 2 的树。但是路径压缩操作只在查询操作时进行,并且也只会压缩单条路线,不会优化整个并查集。
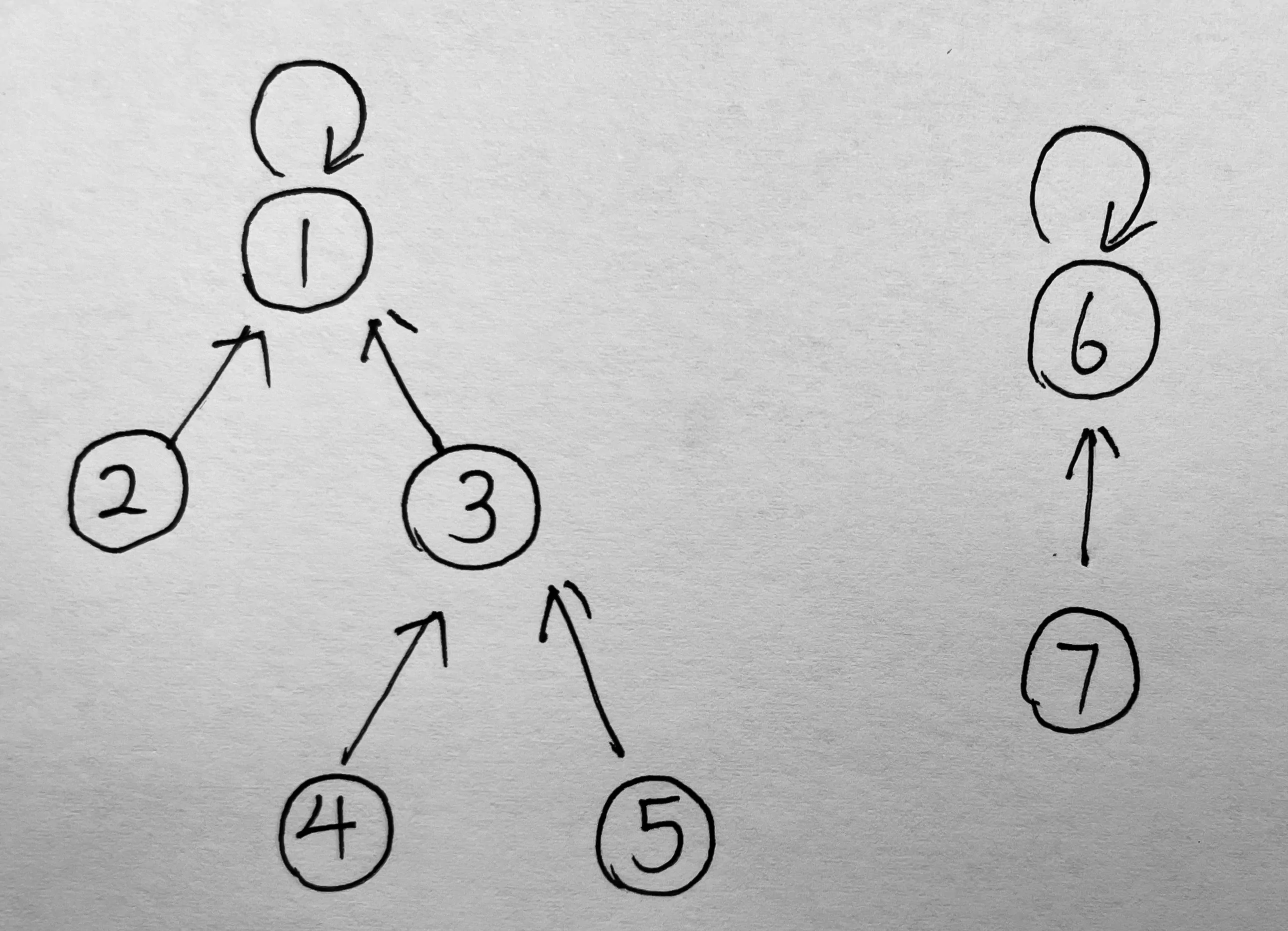
如上图,如果我们要合并这两个树,如果将 6 合并到 1,会得到下图左边的结果,深度为 3,如果将 1 合并到 6,会得到下图右边的结果,深度为 4。由此可见,如何合并两个树,对结果的深度有影响。
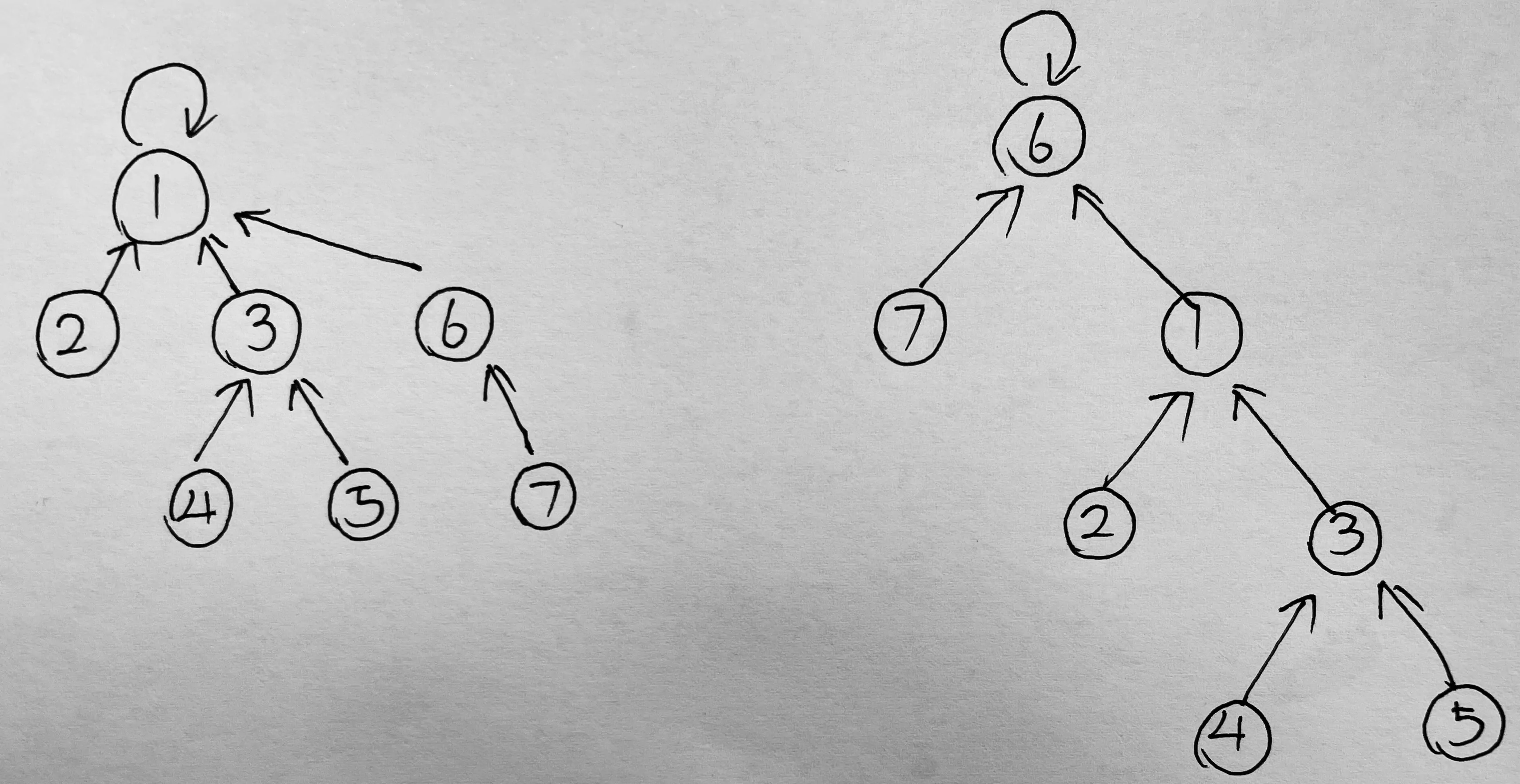
为了查询效率我们当然要让树的深度越小越好,简单分析可以得到,应当将深度小的树合并到深度大的树,这样深度不变。如果两树深度相同,那么如何合并结果是一样的,深度都会增大 1。我们要比对树的深度,因此需要额外的数组 rnk[ ] 来保存该节点的子树的深度。
int fa[MAXN], rnk[MAXN];
void init(int n)
{
for (int i = 1; i <= n; i++)
{
fa[i] = i;
rnk[i] = 1;
}
}
int find(int x)
{
return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
void merge(int i, int j)
{
int x = find(i), y = find(j);
if (x == y)
return;
if (rnk[x] < rnk[y])
swap(x, y);
fa[y] = x;
if (rnk[x] == rnk[y])
rnk[x]++;
}第一个 if 控制合并方式,将深度小的树合并到深度大的树。
第二个 if 维护 rnk[ ] 数组,当深度相同两树合并时,深度才会 +1。
1.3.3 启发式合并(按节点数)
不可能出现一个集合,节点数更少的同时深度更浅,因此,按节点数也能够实现启发式合并。
维护各联通集合的元素数量,元素数量另开辟一个数组储存,并且储存到根节点上。
易错点:merge 函数,当两元素在同一集合,需要跳过操作,否则集合元素数量会错误翻倍。
int fa[MAXN], sz[MAXN];
void init(int n)
{
for (int i = 1; i <= n; i++)
{
fa[i] = i;
sz[i] = 1;
}
}
int find(int x)
{
return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
void merge(int i, int j)
{
int x = find(i), y = find(j);
if (x == y)
return;
if (sz[x] < sz[y])
swap(x, y);
fa[y] = x;
sz[x] += sz[y];
}1.4 可额外维护项目
1.4.1 集合元素数量
按节点数的启发式合并维护好了集合元素数量,直接使用即可。
1.4.2 到根节点的距离
维护各节点到根节点的距离,距离另开辟一个数组储存,且储存到对应节点上。
易错点:merge 函数,修改 fa 和 ds 前一定要储存好父节点,否则会出错。因为更新后再运行 find 函数,结果会变化。
int fa[MAXN], ds[MAXN];
void init(int n)
{
for (int i = 1; i <= n; i++)
fa[i] = i;
}
int find(int n)
{
if (fa[n] == n)
return n;
int res = find(fa[n]); // 先路径压缩
ds[n] += ds[fa[n]]; // 再更新距离
return fa[n] = res; // 再路径压缩
}
void merge(int a, int b, int r) // r为两节点的距离关系
{
int faa = find(a), fab = find(b); // 一定要先储存好父节点,否则下面更新后会变化。
fa[faa] = fab;
ds[faa] = ds[b] - ds[a] + r;
}例题
POJ2524 - Ubiquitous Religions: http://poj.org/problem?id=2524
2 种类并查集
有时候,我们并不知道哪些元素应该为一类,只知道哪些元素不能为一类,此时一般并查集就没法处理这种问题了。
2.1 分析
借助第一个例题来具体分析:已知虫子有两种性别,我们简称为 A、B。输入告诉我们有几只虫子,也告诉我们这几只虫子之间的配对关系,也就是性别不同进行配对,然后我们需要判断这种配对关系是否出现矛盾(即出现了同性配对的情况)。
我们可以发现,如果我们想用一般并查集把虫子分成 A、B 两类,就会发现每组配对关系,到底谁是 A 谁是 B 是不确定的,那这就没法解决了。
这时就要用到种类并查集,种类并查集的所有代码都和一般并查集一样,不同的是使用方法。
2.2 初始化
本题有两种性别,那么就要初始化两倍大小的并查集。$1\sim N$ 和 $N+1\sim 2N$ 就可以表示出两种性别。(第二个例题有三个种类,那就得开三倍大小)

2.3 合并
例如我们要表示 1、2 虫配对,即 1、2 虫不能为同性,我们就要将 1 和 6、5 和 2 合并。推广来说,如果要配对 $A$、$B$,那么就要合并 $A$ 和 $B+N$、$A+N$ 和 $B$。
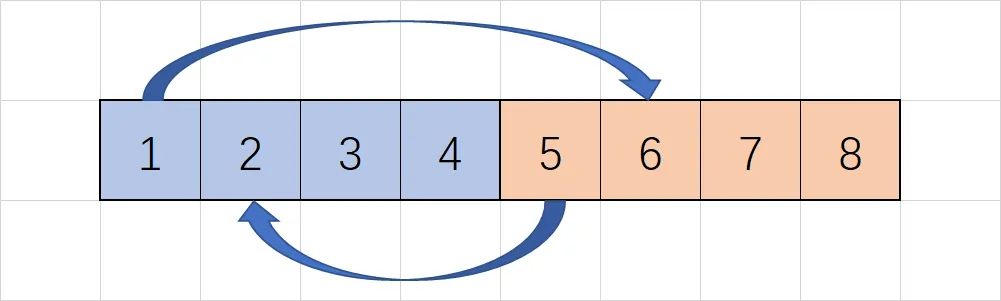
注意:需要注意合并的方向,有时合并的方向会影响题目的结果,最好是一次合并实点到虚点、一次合并虚点到实点。
如果再表示 2、4 虫配对,那么就再将 2 和 8、6 和 4 合并。

于是 1、4 虫就通过 6 间接连接到了一起,2 通过 5 与 8 建立关系,最后 1、4、(6) 为一组,2、(5)、(8) 为一组。
那我们如何判断是否有矛盾呢?只需要判断两虫是否在同一组即可,因为同一组的含义为。例如我们将 1、4 配对,发现 1、4 在同一组(即 find(1) == find(4)),那么就表明出现矛盾。于是本题只需每次添加新关系时,判断 find(a) == find(b) 就能得知是否有矛盾了。
例题
POJ2492 - A Bug's Life: http://poj.org/problem?id=2492
POJ1182 - 食物链: http://poj.org/problem?id=1182
本文采用 CC BY-SA 4.0 许可,本文 Markdown 源码:Haotian-BiJi