算法 | Manacher

Manacher (manachar, 马拉车)：在 $O(n)$ 时间内计算一个字符串内所有回文子串的算法。

回文半径

先介绍一个概念——回文半径，它是回文串的中心（“对称轴”）到回文串两端的长度。

它分为两类，一种是奇回文半径和偶回文半径，分别表示长度为奇数的回文串半径和长度为偶数的回文串半径。之所以与长度的奇偶性有关系，是因为长度为奇数时，回文串的“对称轴”恰好落在一个字符上，而长度为偶数时，“对称轴”落在字符之间。这两种情况在计算时有细节差异，因此得分开考虑。

例如对于奇数长度的回文串，回文半径是：$\stackrel{3}{\overbrace{aw\underset{\hat{}}{a}}}wa$ (字符下面的标记代表考虑的对称位置)

而对于偶数长度的回文串，就有所差别：$\stackrel{3}{\overbrace{aaw}}\underset{\hat{}}{w}aa$

下面一个示例给出了奇回文半径和偶回文半径的差异：

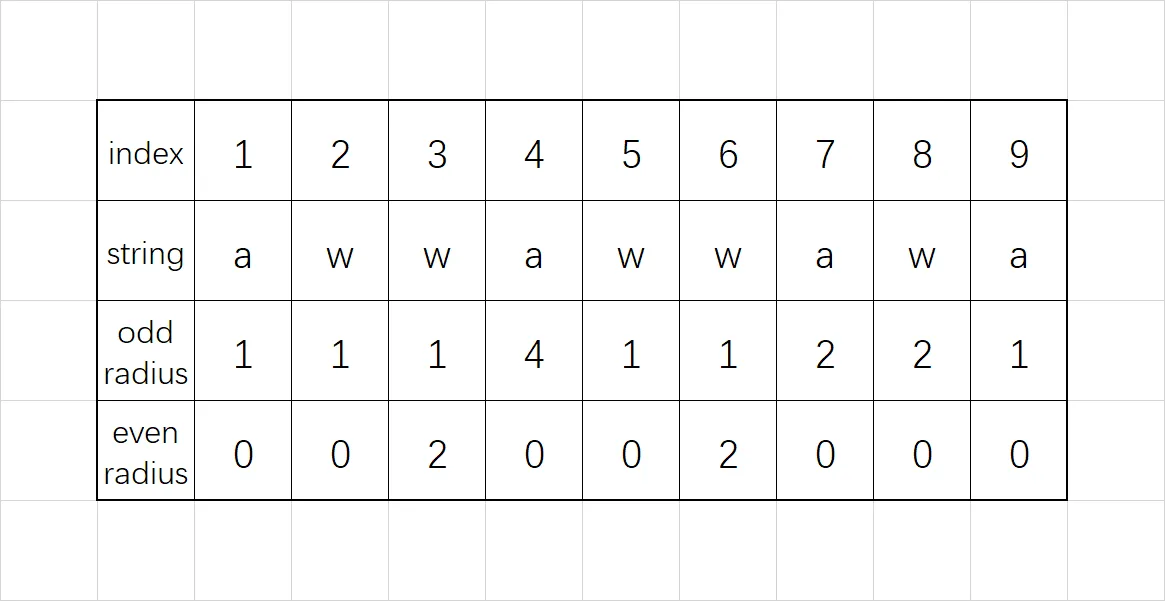
统一化

上面可以看到，回文串的长度奇偶性会造成许多细节差异，导致代码实现非常麻烦，接下来介绍将这两种情况统一的方法。

对于一个长度为 $x$ 的字符串，向它的首尾和每个字符之间插入一个字符，该字符必须在原串中不存在（否则会产生干扰）：

• awawa $\Rightarrow$ #a#w#a#w#a#

这样，就向其中插入了 $x+1$ 个字符，现在字符串长度为 $2x+1$ 一定是奇数了，因此就可以只考虑奇回文半径了。

为了实现方便，字符串下标从 $1$ 开始更好，所以再向首尾插入一个在原串中不存在的字符，且首尾要不一样（否则会产生干扰）：

• #a#w#a#w#a# $\Rightarrow$ ^#a#w#a#w#a#$

这样，奇数长度和偶数长度的字符串都统一成奇数长度了。如果想要恢复原串，再把插入的过滤掉就行了。

string pre_process(string &s)
{
    string ans = "^";
    for (auto &c : s)
    {
        ans += '#';
        ans += c;
    }
    ans += '#';
    ans += '$';
    return ans;
}

综上，下面的介绍都只介绍计算奇数长度的方法，需要先进行预处理统一后再使用。

朴素算法（中心扩展法）

在介绍马拉车算法前，先介绍解决上面这个问题的朴素算法，即中心扩展法。

中心扩展法的流程是：

• 对字符串内每一位字符 $a_i$，进行下面的操作：

  • 以 $a_i$ 为中心，向左右进行扩展，直到发现 $a_{i-j}\ne a_{i+j}$ 或到达边缘则停止。
  • 记该字符的回文半径 $r_i=j-1$.

这个算法的时间复杂度显然为 $O(n^2)$，性能较差。

manacher 算法

manacher 算法的核心思想就是充分利用已经计算过的部分推导出还没计算的部分，避免重复计算。

manacher 算法计算一位的回文半径有三种方法，在三种不同情况下使用：

• 直接对称
• 对称 + 中心扩展
• 直接中心扩展

直接对称

假设目前已经计算得到一个大回文串，且大回文串左侧的回文半径已经计算出了了。如果左侧某个位置的回文半径对应的回文串与大回文串的边界不重合，那么这个位置对称到右侧的回文半径与左侧相等。

用形式化的说法，如果目前已知的边界最靠右的回文串为 $[s,t]$，它的中心为 $m$，并且 $r_1,r_2,\dots ,r_m$ 已经计算完成，那么如果要计算 $(m,t]$ 区间的回文半径 $r_{m+i}$，那么考察关于中心 $m$ 对称的回文半径 $r_{m-i}$，如果 $(m-i)-r_{m-i}+1>s$，那么就可以直接令 $r_{m+i}=r_{m-i}$.

这种情况的示意图如下：

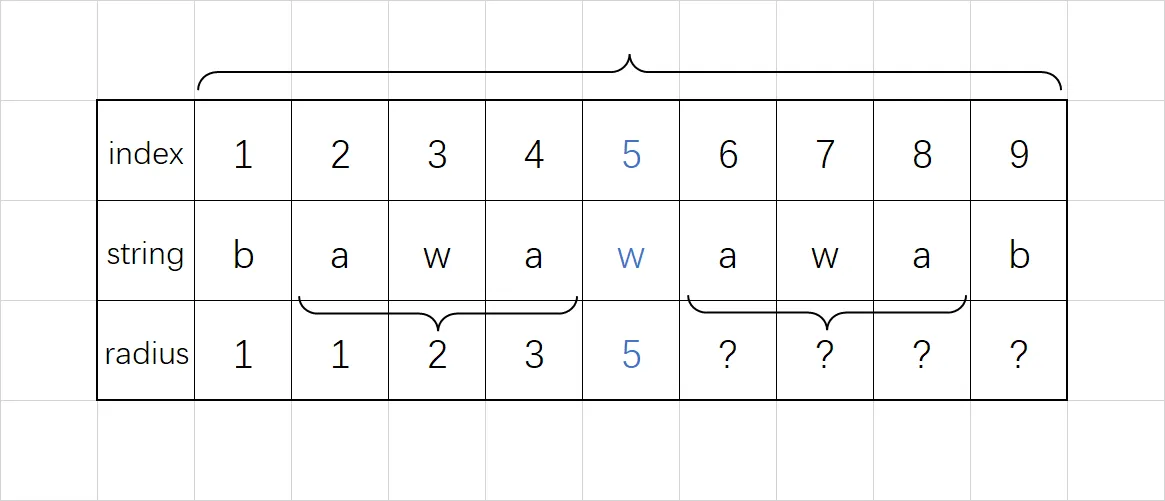
使用这个方法，可以直接令 $r_6=r_4,r_7=r_3,r_8=r_2$，最后填好后的回文半径如下：

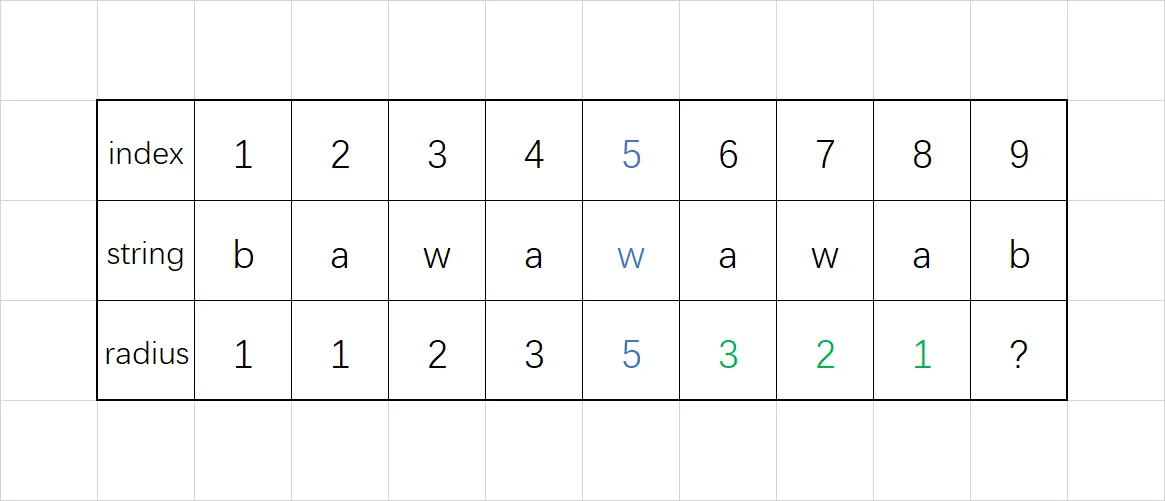
为什么不令 $r_9=r_1$ 是因为它不满足这个情况的限制，因为 $r_1$ 所代表的回文串已经接触到了大回文串的边界。

注意，在每次计算 $r_i$ 完成后，需要更新边界最靠右的回文串。

对称 + 中心扩展

假设目前已经计算得到一个大回文串，且大回文串左侧的回文半径已经计算出了了。如果左侧某个位置的回文半径对应的回文串与大回文串的边界重合，那么先将这个位置的回文半径取为到大回文串边界的距离，再用中心扩展法尝试扩展。

用形式化的说法，如果目前已知的边界最靠右的回文串为 $[s,t]$，它的中心为 $m$，并且 $r_1,r_2,\dots ,r_m$ 已经计算完成，那么如果要计算 $(m,t]$ 区间的回文半径 $r_{m+i}$，那么考察关于中心 $m$ 对称的回文半径 $r_{m-i}$，如果 $(m-i)-r_{m-i}+1\le s$，那么先令 $r_{m+i}=t-(m+i)+1$，然后再用中心扩展法尝试扩展。

这种情况的示意图如下：

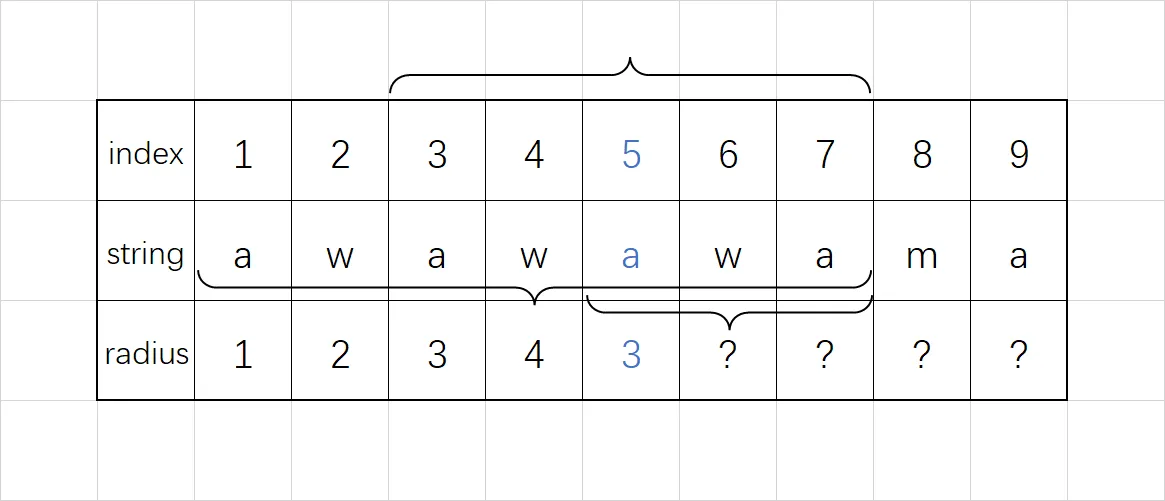
为什么这种情况不能直接对称过来赋值呢？其实上面这个示意图已经展现出来了，如果将右侧这个赋值为 $4$，那很明显 $\text{awawama}$ 并不是回文串。因为对于右边还没考虑到的部分，我们没有足够的信息来断言在对称位置的回文串具有同样的长度。

使用这个方法，可以直接令 $r_6=7-6+1=2,r_7=7-7+1=1$，然后再用中心扩展法尝试扩展（但并不能成功扩展），最后填好后的回文半径如下：

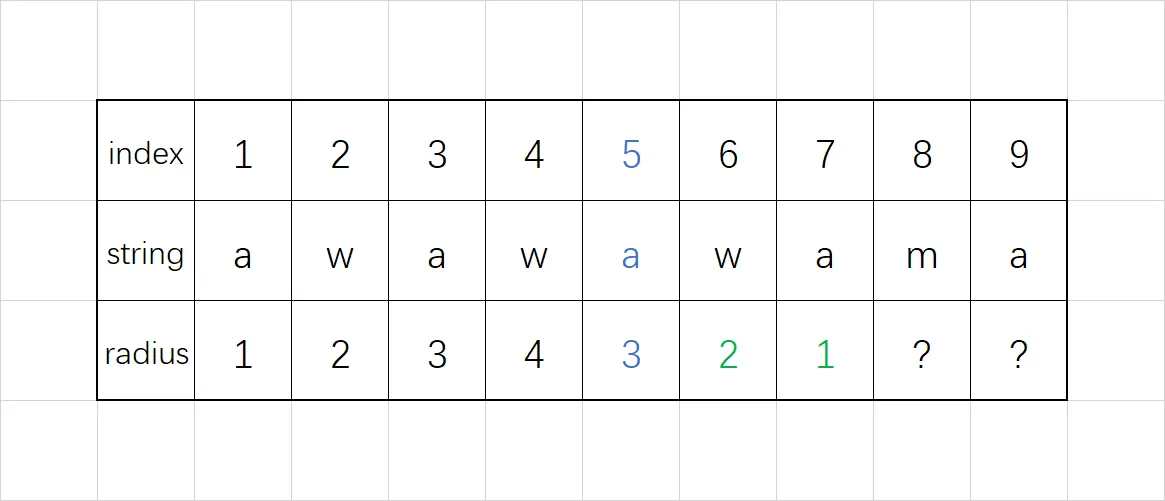
注意，在每次计算 $r_i$ 完成后，需要更新边界最靠右的回文串。

直接中心扩展

对于没有包含在大回文串里的部分，那就只能用中心扩展法了。对应的情况示例如下：

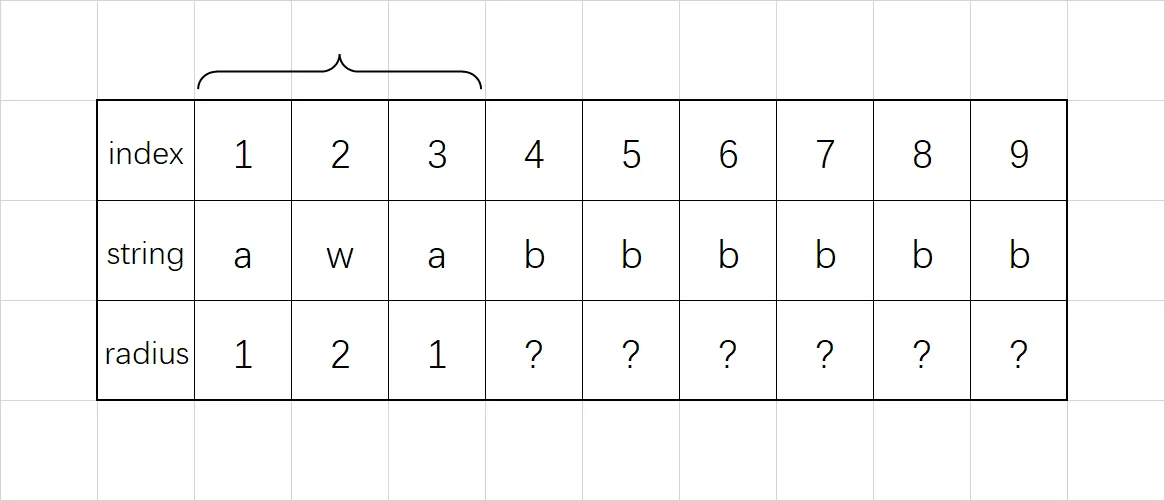
注意，在每次计算 $r_i$ 完成后，需要更新边界最靠右的回文串。

代码实现

前面说那么复杂，其实代码很简单，三种情况分类讨论其实用一个三元表达式就搞定了。代码内 r 代表当前边界最靠右的回文串右边界，mid 是当前边界最靠右的回文串的中心。

// s - 字符串（下标1开始，需要预处理）
// p - 对应位置回文半径
void manacher(string &s, vector<int> &p)
{
    int r = 0, mid = 0;
    for (int i = 1; i < s.size() - 1; i++)
    {
        p[i] = r > i ? min(p[2 * mid - i], r - i) : 1;
        while (s[i + p[i]] == s[i - p[i]])
            p[i]++;
        if (i + p[i] > r)
        {
            r = i + p[i];
            mid = i;
        }
    }
}