2023牛客暑期多校训练营8

I - Make It Square

https://ac.nowcoder.com/acm/contest/57362/I

题意

给定串 $S$ 和 $T$，问有多少种长度均为 $i$ 的串 $P,Q$，使得 $\mathrm{concat}(P,S,Q,T)$ 为一个 AA 型的串，其中 A 为一任意非空字符串。可用字符集为小写字母。对 $i\in[1,m]$ 求出答案。$1\leq m\leq 10^6$，$1\leq|S|,|T|\leq 10^6$。

题解

特殊情况

首先特判掉几个特殊情况，从而将问题拆分简化。

  • $|S|=|T|$

由于 $|P|=|Q|,\;|S|=|T|$，那么字符串正好从中间分开，满足 $P+S=Q+T$，即满足 $P=Q,\;S=T$.

那么可以直接判断：如果 $S\neq T$，答案均为 $0$；如果 $S=T$，答案为 $26^m$.

  • $|S|+|T|$ 为奇数

由于 $|P|=|Q|$ 且 $|S|+|T|$ 为奇数，那么 $|P+S+Q+T|$ 一定为奇数，不满足题目条件，答案均为 $0$.

$|S|>|T|$ 的情况

这种情况的示意图如下，为了方便，令 $|P|=|Q|=i,\;|S|=a,\;|T|=b$：

由于要求整个字符串从中心分开后，两个子串一致。因此我们把上面这个字符串从中心切成两半，再对齐摆到一起，此时两个字符串的对应位置应该时相等的。

  1. 若 $\frac{a-b}{2}-i>0$，那么这个图的样子如下（图中标注的均为长度）：

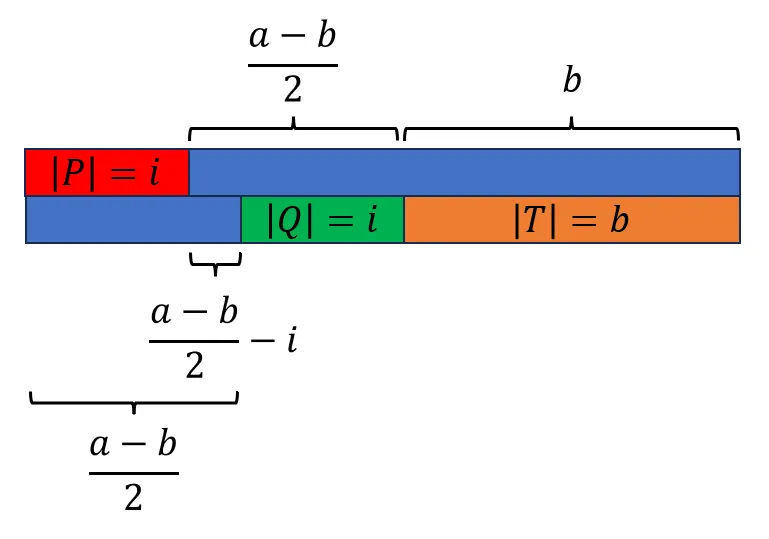
上面两行代表的字符串必须对应位置相对，而 $S$ 和 $T$ 有交叉的部分从图上看有两个：长度为 $b$ 的一段、长度为 $\frac{a-b}{2}-i$ 的一段。

因此如果要满足题目条件，那么 $S$ 和 $T$ 对应位置必须满足以下条件（中括号代表按下标取子串）：

  • $S[\frac{a-b}{2}\dots (\frac{a-b}{2}+b-1)]=T[0\dots (b-1)]$
  • $S[0\dots (\frac{a-b}{2}-i-1)]=S[(a-\frac{a-b}{2}+i)\dots (a-1)]$

如果 $S$ 和 $T$ 不满足上面两个条件，那么这种情况数为 $0$.

如果 $S$ 和 $T$ 满足上面两个条件，可以发现 $P$ 和 $Q$ 的位置已经被 $S$ 字符串定死了，因此只有一种情况，情况数为 $1$.

对于如何判断是否符合上面的条件，第一条直接遍历判断就行，复杂度为 $O(n)$，而对于第二条，就不能遍历判断了，因为 $i\in[1,m]\;且\;1\leq m\leq 10^6$，如果对于每个 $i$ 执行一次，那么复杂度会来到 $O(n^2)$.

第二条的含义是字符串 $S$ 的长度为 $\frac{a-b}{2}-i$ 的前缀和后缀是否相等，这个正好可以用 KMP 算法在 $O(n)$ 时间内解决。将 $S$ 作为模式串用 KMP 算法计算一遍部分匹配表，然后根据部分匹配表就可以得到 $S$ 串的所有前后缀相对的长度。对于每个 $i$ 直接查询 $\frac{a-b}{2}-i$ 这个长度在不在答案内即可。

  1. 若 $\frac{a-b}{2}-i\leq0$，那么这个图的样子如下：

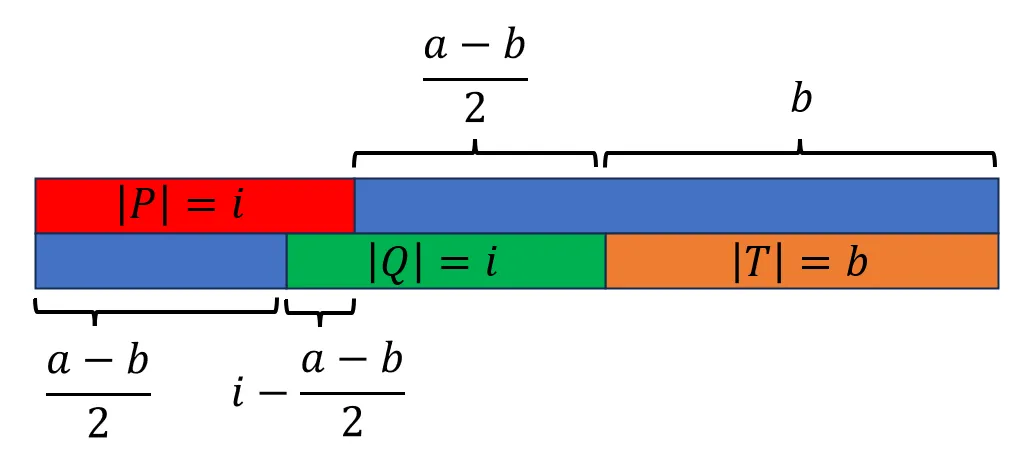
可以发现，此时 $S$ 和 $T$ 有交叉的部分只有一个：长度为 $b$ 的一段。

那么如果要满足题目条件， $S$ 和 $T$ 对应位置只用满足：

  • $S[\frac{a-b}{2}\dots (\frac{a-b}{2}+b-1)]=T[0\dots (b-1)]$

如果 $S$ 和 $T$ 不满足上面的条件，那么这种情况数为 $0$.

如果 $S$ 和 $T$ 满足上面的条件，可以发现 $P$ 和 $Q$ 的位置一部分被 $S$ 定死了，而中间有一段长度为 $i-\frac{a-b}{2}$ 交叉的地方，是可以自由取值的，那么情况数为：$26^{i-\frac{a-b}{2}}$.

$|S|<|T|$ 的情况

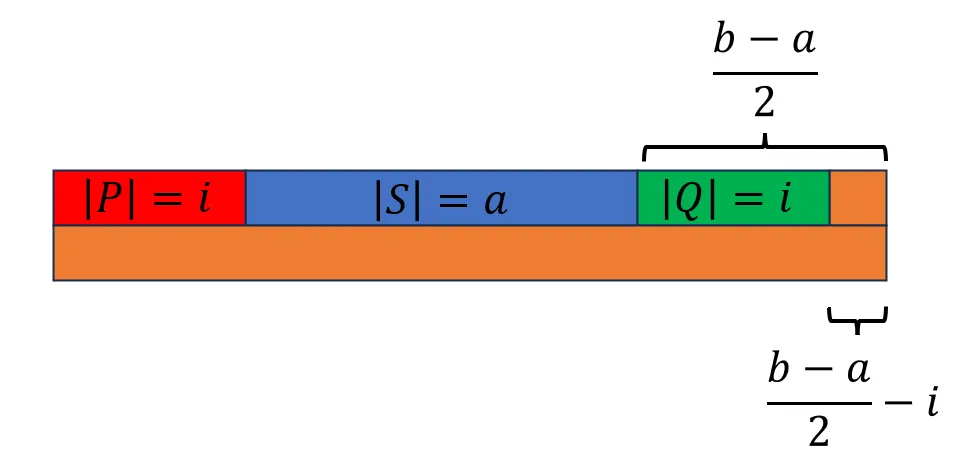
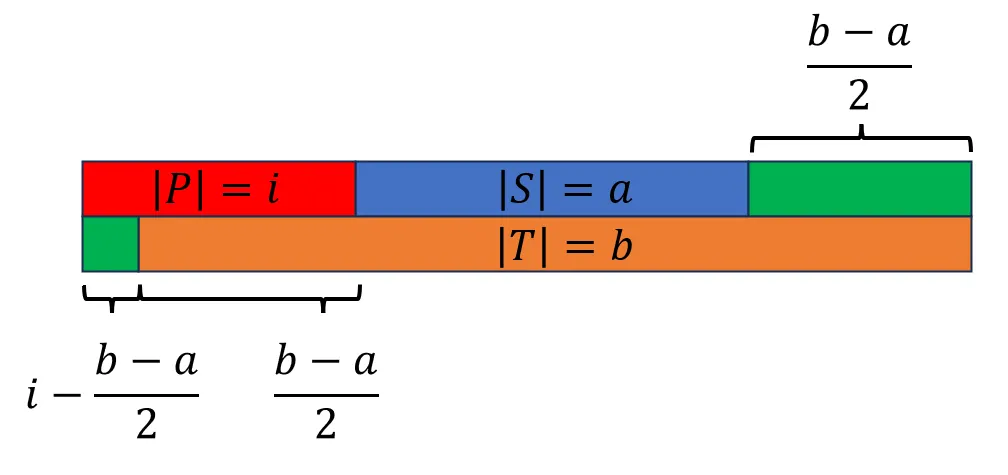
这种情况的示意图如下：

这种情况实际上和上面的思考方式完全一致，实际上代码只需要改几个变量名就行了，因此下面只放出来示意图，不再解释。

  1. $\frac{b-a}{2}-i>0$

  1. $\frac{b-a}{2}-i\leq0$

代码

#include <bits/stdc++.h>
#define endl '\n'
#define int long long

using namespace std;

constexpr int MOD = 998244353;

class KMP
{
    vector<int> nxt;
    string pat;

public:
    KMP(string &s)
    {
        pat = s;
        int n = pat.length();
        int j = 0;
        nxt.resize(n);
        for (int i = 1; i < n; i++)
        {
            while (j > 0 && pat[i] != pat[j])
                j = nxt[j - 1];
            if (pat[i] == pat[j])
                j++;
            nxt[i] = j;
        }
    }
    vector<int> find(string &txt)
    {
        int n = pat.length(), m = txt.length();
        int j = 0;
        vector<int> ans;
        for (int i = 0; i < m; i++)
        {
            while (j > 0 && txt[i] != pat[j])
                j = nxt[j - 1];
            if (txt[i] == pat[j])
                j++;
            if (j == n)
            {
                ans.push_back(i - n + 1);
                j = nxt[j - 1];
            }
        }
        return ans;
    }
    set<int> get_border()
    {
        set<int> s;
        int cur = nxt.back();
        while (cur)
        {
            s.insert(cur);
            cur = nxt[cur - 1];
        }
        s.insert(0);
        return s;
    }
};

void solve()
{
    int m;
    cin >> m;
    string s, t;
    cin >> s >> t;
    int ls = s.size(), lt = t.size();
    if (ls == lt)
    {
        if (s != t)
        {
            for (int i = 1; i <= m; i++)
                cout << 0 << " \n"[i == m];
        }
        else
        {
            int ans = 1;
            for (int i = 1; i <= m; i++)
            {
                ans = ans * 26 % MOD;
                cout << ans << " \n"[i == m];
            }
        }
        return;
    }
    if ((ls + lt) % 2 == 1)
    {
        for (int i = 1; i <= m; i++)
            cout << 0 << " \n"[i == m];
        return;
    }
    if (ls > lt)
    {
        for (int i = lt - 1, j = ls - 1 - (ls - lt) / 2; i >= 0; i--, j--)
        {
            if (t[i] != s[j])
            {
                for (int i = 1; i <= m; i++)
                    cout << 0 << " \n"[i == m];
                return;
            }
        }
        int ans = 1;
        KMP kmp_s(s);
        auto border_s = kmp_s.get_border();
        for (int i = 1; i <= m; i++)
        {
            if (i > (ls - lt) / 2)
            {
                ans = ans * 26 % MOD;
                cout << ans << " \n"[i == m];
            }
            else
            {
                if (border_s.count((ls - lt) / 2 - i) == 0)
                    cout << 0 << " \n"[i == m];
                else
                    cout << 1 << " \n"[i == m];
            }
        }
    }
    else // if (ls <= lt)
    {
        for (int i = ls - 1, j = lt - 1 - (lt - ls) / 2; i >= 0; i--, j--)
        {
            if (s[i] != t[j])
            {
                for (int i = 1; i <= m; i++)
                    cout << 0 << " \n"[i == m];
                return;
            }
        }
        int ans = 1;
        KMP kmp_t(t);
        auto border_t = kmp_t.get_border();
        for (int i = 1; i <= m; i++)
        {
            if (i > (lt - ls) / 2)
            {
                ans = ans * 26 % MOD;
                cout << ans << " \n"[i == m];
            }
            else
            {
                if (border_t.count((lt - ls) / 2 - i) == 0)
                    cout << 0 << " \n"[i == m];
                else
                    cout << 1 << " \n"[i == m];
            }
        }
    }
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t--)
        solve();
    return 0;
}