Codeforces Round 897 (Div. 2)

D. Cyclic Operations

https://codeforces.com/contest/1867/problem/D

1 second / 256 megabytes

standard input / standard output

Problem

Egor has an array $a$ of length $n$, initially consisting of zeros. However, he wanted to turn it into another array $b$ of length $n$.

Since Egor doesn't take easy paths, only the following operation can be used (possibly zero or several times):

  • choose an array $l$ of length $k$ ($1 \leq l_i \leq n$, all $l_i$ are distinct) and change each element $a_{l_i}$ to $l_{(i\%k)+1}$ ($1 \leq i \leq k$).

He became interested in whether it is possible to get the array $b$ using only these operations. Since Egor is still a beginner programmer, he asked you to help him solve this problem.

The operation $\%$ means taking the remainder, that is, $a\%b$ is equal to the remainder of dividing the number $a$ by the number $b$.

Input

The first line of the input contains an integer $t$ ($1 \leq t \leq 10^5$) - the number of test cases.

Each test case consists of two lines. The first line contains two integers $n$ and $k$ ($1 \leq k \leq n \leq 10^5$).

The second line contains the array $b_1, b_2, \ldots, b_n$ ($1 \leq b_i \leq n$).

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$.

Output

For each test case, output "YES" (without quotes) if there is a way to get the array $b$ using only the given operation. Otherwise, output "NO" (without quotes). You can output each letter in any case (lowercase or uppercase). For example, the strings "yEs", "yes", "Yes" and "YES" will be accepted as a positive answer.

Example

Input

6
5 3
2 3 5 3 4
4 2
2 4 3 1
1 1
1
3 1
1 2 3
5 3
5 4 3 2 1
6 1
1 2 3 1 5 6

Output

YES
NO
YES
YES
NO
NO

Note

Let's consider the first example:

  • Apply the operation with $l$ = $[1,2,3]$. Now $a$ = $[2,3,1,0,0]$.
  • Apply the operation with $l$ = $[3,5,4]$. Now $a$ = $[2,3,5,3,4]$ = $b$.

We see that it is possible to get the array $b$. Therefore, the answer is .In the second example, it can be proven that the array $b$ cannot be obtained, therefore the answer is NO.

题解

首先，要注意到对于一个完整的置换环，是没有任何方法增加或减少它的长度的，因此所有环长必须 $=k$ 才合法。

例如对于 $b=[3,\underline3,\underline5,2,\underline2]$，标记下划线的便是一个完整的置换环，它对应的 $l$ 是唯一的，一定是 $[2,3,5]$，因此 $k$ 的大小必须为 $3$.

因此，首先需要找到 $b$ 中所有的环，判断环长是否都 $=k$，如果出现一个不等，则不成立输出 No.

对于不在环中的元素，它一定在某个环的支链上，将上面的例子可视化即为：

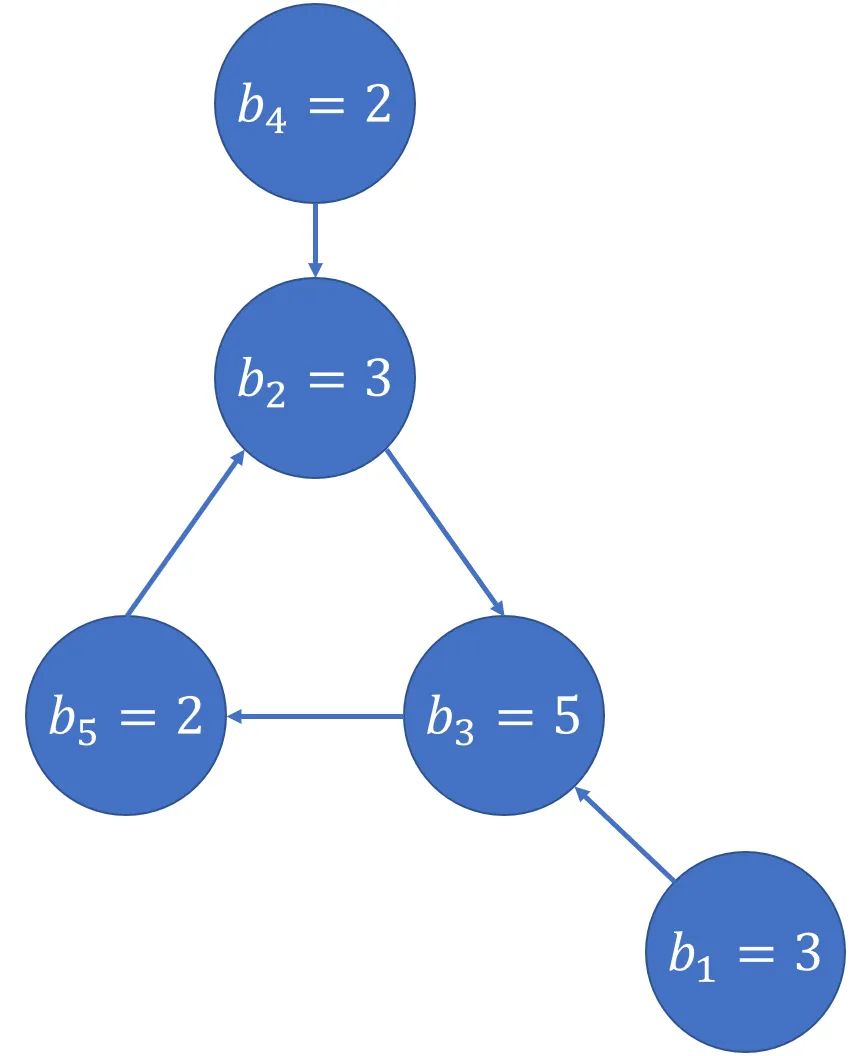
可以看到 $b_2,b_3,b_5$ 是环，不在环上的元素 $b_1,b_4$ 都是环的一个支链。

由于不同操作可以互相覆盖，那么不管链有多长，一定能找到一种构造方式将链构造出来。

例如对于上面的例子，如果 $k=3$，那么支链比 $k$ 小，但是这个链可以借助环上的元素，构造一个长度为 $k$ 的环，即可将这个链构造出来：

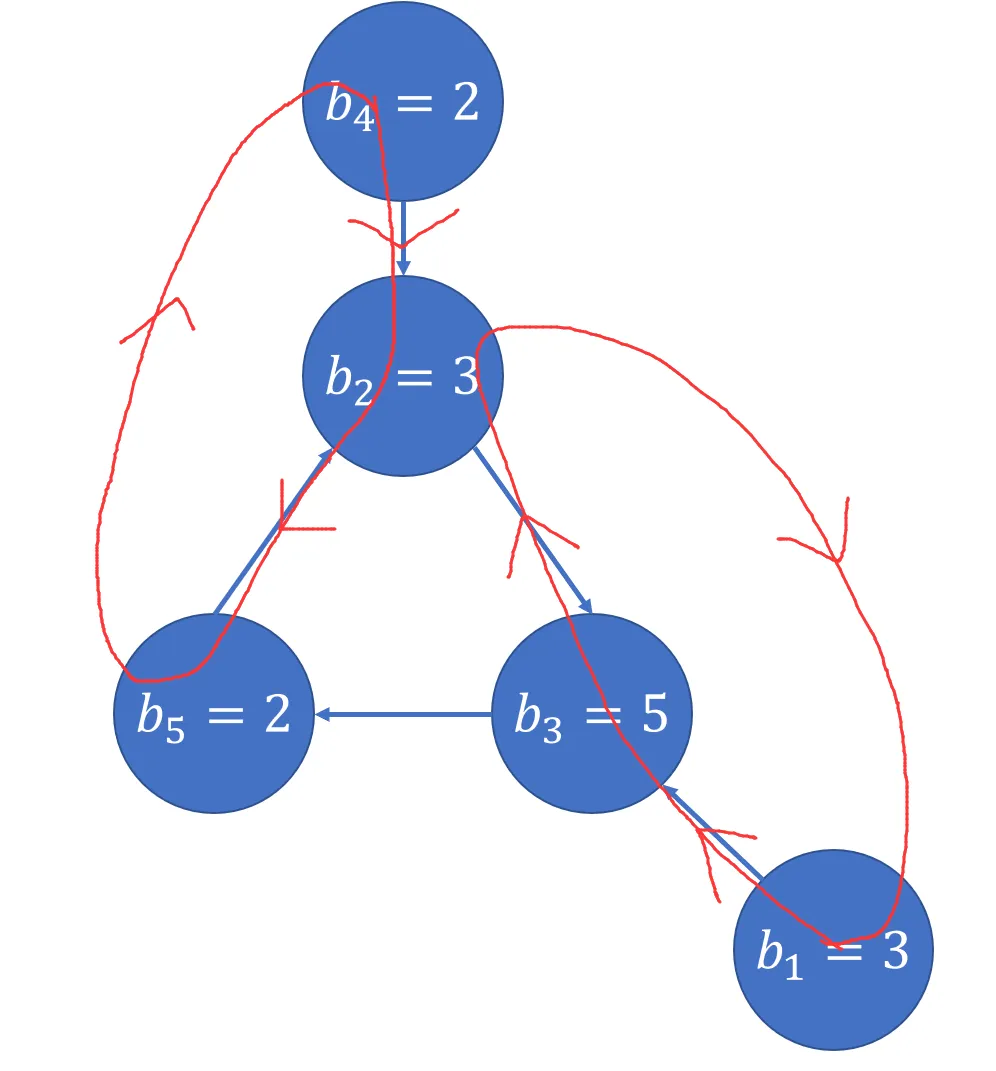
将链构造完后，环上数字不一定满足条件，不过只要再构造一遍环，环上的数字就会被覆盖成正确的了。

例如对于 $b=[2,1,1,3,4,5,6]$，$k=2$：

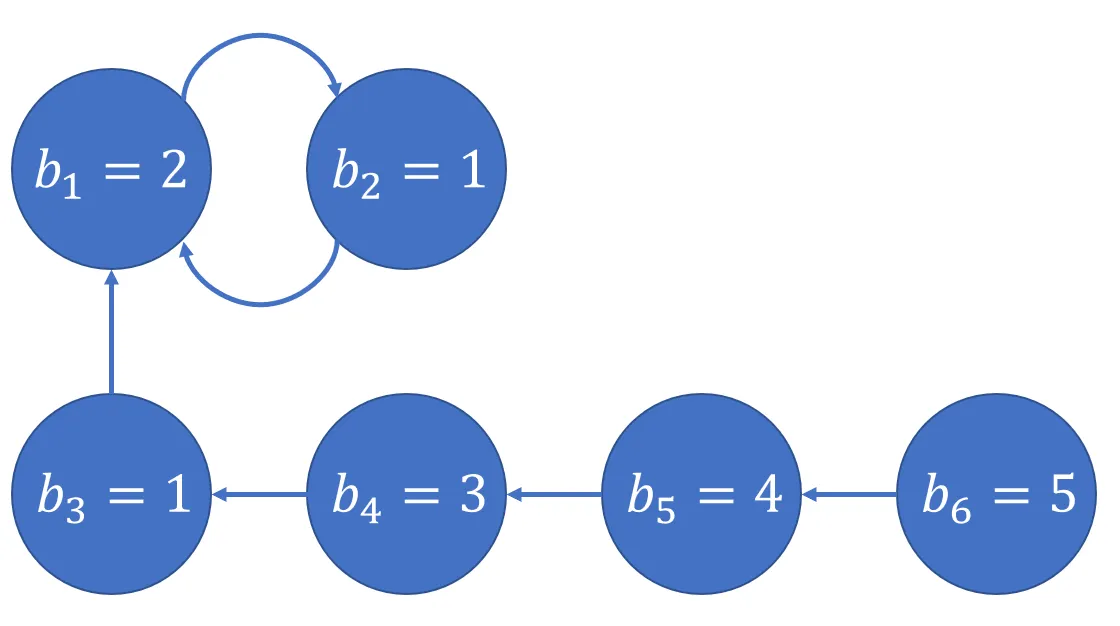
如上图可见支链很长，已经比 $k$ 大了，但是这个链可以被拆成一个一个首尾相接的长度为 $k$ 的环，按远端到近端的操作顺序进行操作，那么这个链最终就能被构造出来：

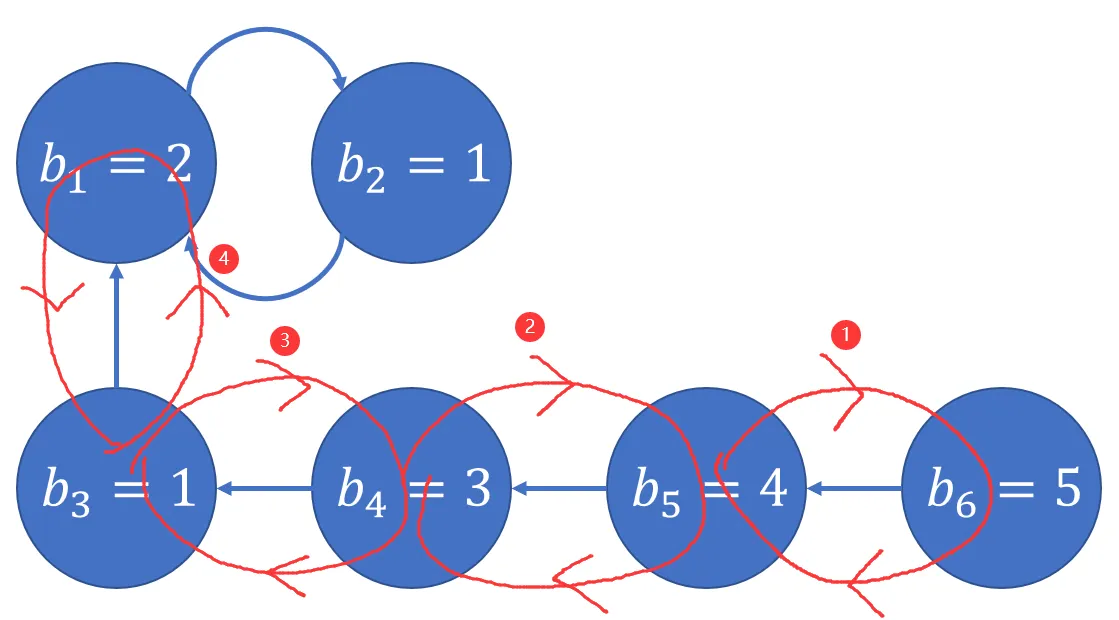
将链构造完后，环上数字不一定满足条件，不过只要再构造一遍环，环上的数字就会被覆盖成正确的了。

易错点

如果到这里你没有发现一些纰漏，那么就会掉到一个坑里了，好在本题样例里面有这个坑，很容易检查出来。

这个问题就是，对于 $k=1$ 的情况，我们上面的分析都免谈，因为 $k=1$ 只有一种可能就是成自环。

因此，需要特判 $k=1$ 的情况，如果 $b_i=i$ 对于所有 $i$ 成立，则可以构造，反之不合法，输出 No.

代码

#include <bits/stdc++.h>
#define endl '\n'
// #define int long long
 
using namespace std;
 
void solve()
{
    int n, k;
    cin >> n >> k;
    vector<int> nxt(n + 10);
    for (int i = 1; i <= n; i++)
        cin >> nxt[i];
    if (k == 1)
    {
        for (int i = 1; i <= n; i++)
        {
            if (nxt[i] != i)
            {
                cout << "NO" << endl;
                return;
            }
        }
        cout << "YES" << endl;
        return;
    }
    vector<int> idx(n + 10), cir(n + 10);
    for (int i = 1; i <= n; i++)
    {
        if (idx[i])
            continue;
        int now = i;
        idx[now] = 1;
        cir[now] = i;
        while (!idx[nxt[now]])
        {
            idx[nxt[now]] = idx[now] + 1;
            cir[nxt[now]] = i;
            now = nxt[now];
        }
        int cnt = idx[now] - idx[nxt[now]] + 1;
        if (cir[nxt[now]] == i && cnt != k)
        {
            cout << "NO" << endl;
            return;
        }
    }
    cout << "YES" << endl;
}
 
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--)
        solve();
    return 0;
}