卷积 (Convolution): 一种结合两个函数形成新函数的方法，即 $h(x)=f(x)*g(x)$.

1 定义与计算

如果我们有两个函数 $f(x)$ 和 $g(x)$，如果我们要将他们组合在一起形成 $h(x)$，有很多种方案。例如：

• 使用加法 $h(x)=f(x)+g(x)$
• 使用乘法 $h(x)=f(x)\cdot g(x)$

卷积其实也是一种结合方式，使用卷积也可以将两个函数结合在一起：$h(x)=f(x)*g(x)$

注：卷积运算常用 $*$ 来表示，请注意它不是乘法。

到这里你可能会莫名其妙，将两个函数组合起来有什么用？加起来、乘起来或者卷积起来这完全没意义啊。

需要注意的是，上面所说的只是组合方式，其具体代表的含义得看具体情况。例如两个函数值代表物品数量，我们要求物品数量的和，那么加法组合就具有了意义。在讨论卷积的意义之前，我们必须先知道卷积是怎么计算的。

对于连续一维卷积：

$$ (f*g)(x)=\int _{-\infty }^{\infty }f(\tau )g(x-\tau )\,d\tau $$

对于离散一维卷积：

$$ (f*g)[x]=\sum _{\tau =-\infty }^{\infty }f[\tau]g[x-\tau] $$

对于离散二维卷积：

$$ (f*g)[x][y]=\sum _{i =-\infty }^{\infty }\sum _{j =-\infty }^{\infty }f[i][j]g[x-i][x-j] $$

上面这些公式有点抽象，只是为了严谨而放出，用具象的例子更好理解。

在计算机科学中，通常讨论的都是离散卷积。在计算机视觉中，通常使用的都是二维卷积。因此用一个二维离散卷积的计算过程举例：

原函数 $f[x][y]$	卷积核 $g[x][y]$

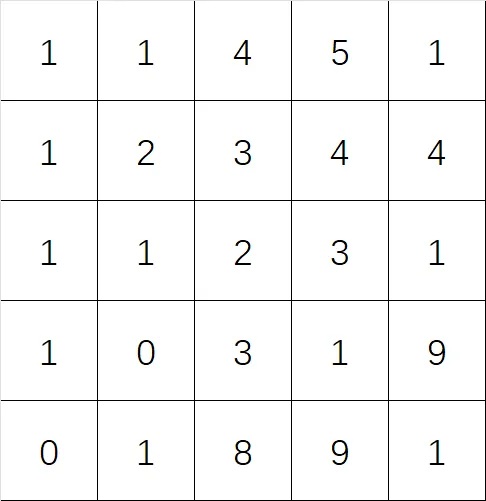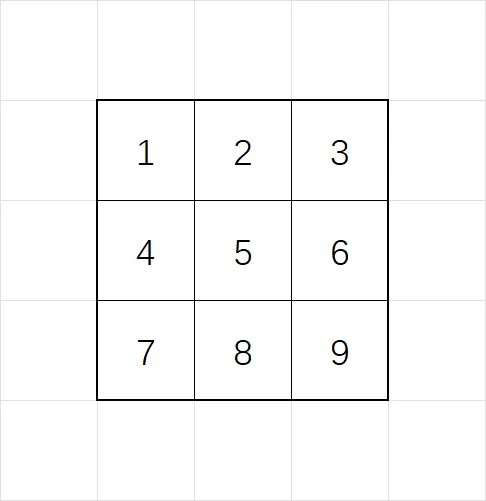第一步，旋转卷积核 $180^{\circ}$：

第二步，将旋转后的卷积核盖在原函数上，例如覆盖在左上角：

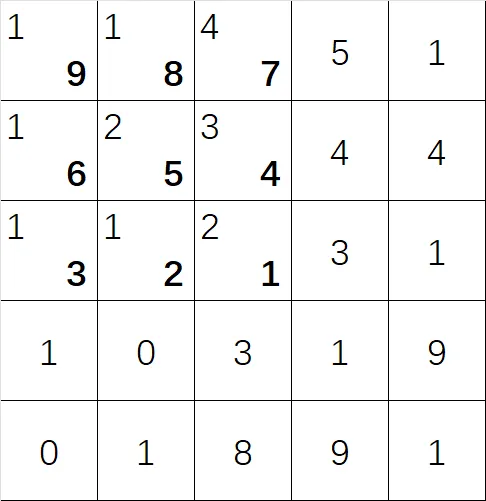
第三步，将原函数和卷积核对应位置相乘，得到结果在求和：

即：$1\times9+1\times8+4\times7+1\times6+2\times5+3\times4+1\times3+1\times2+2\times1=80$，得到的结果便是卷积结果对应位置的值。

这只是执行了卷积的其中一步，记住卷积需要对整个原函数进行操作，因此我们将卷积核在原函数上滑动，计算出最终完整的结果：

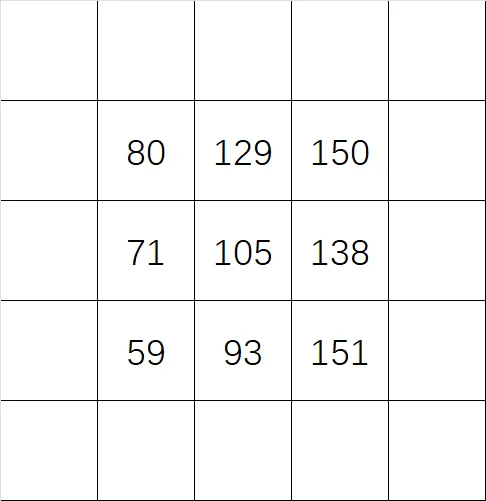
上面便是原函数 $f[x][y]$ 与卷积核 $g[x][y]$ 卷积得到的最终结果了。

但是很快我们会发现一个问题，这结果怎么比原函数少了一圈？究其原因是因为原函数并不是像我们公式所写一样是无限的二维平面，而只是有限的一小块。这就代表一定会产生边界无法进行卷积，因为卷积核在边界会越界。

解决这个问题很简单，扩大一圈边界就行，常见方法有补 $0$ 和对称，把原函数补一圈再卷积就行了：

补 $0$	对称

2 意义

就像加法乘法意义，脱离了具体情形，卷积是没有意义的，我们不能直接说卷积一定是具有什么功能的。

下面讨论的均为二维离散卷积

决定卷积操作意义的是卷积核，卷积核的具体情形决定了卷积操作的功能。

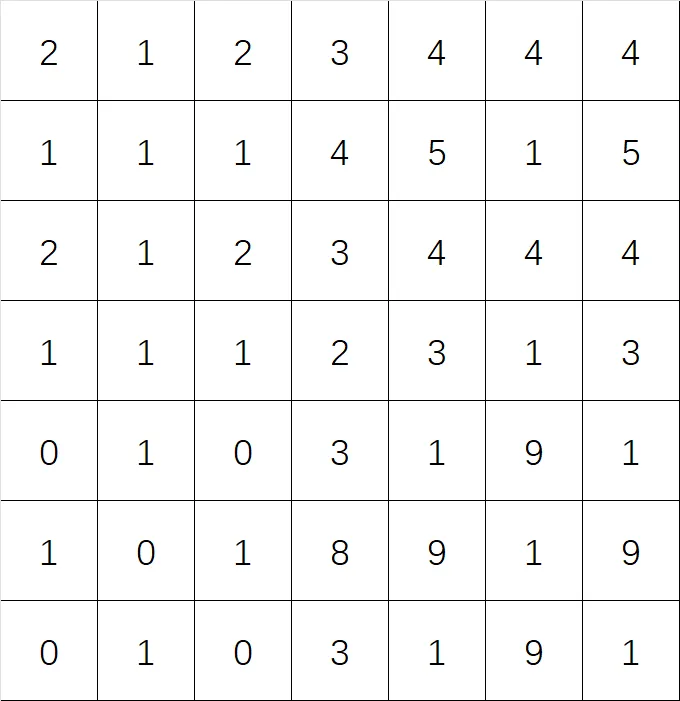
例如下面这个卷积核，它的意义便是对原函数取平均：

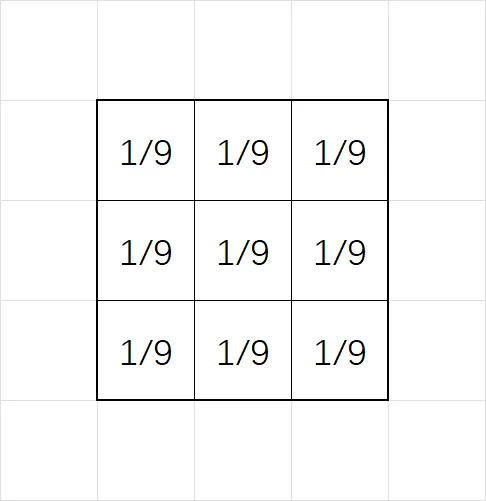
又例如下面这个卷积核，它的意义也是平均，不过它并不是上面展示的均匀平均，而是进行高斯平均：

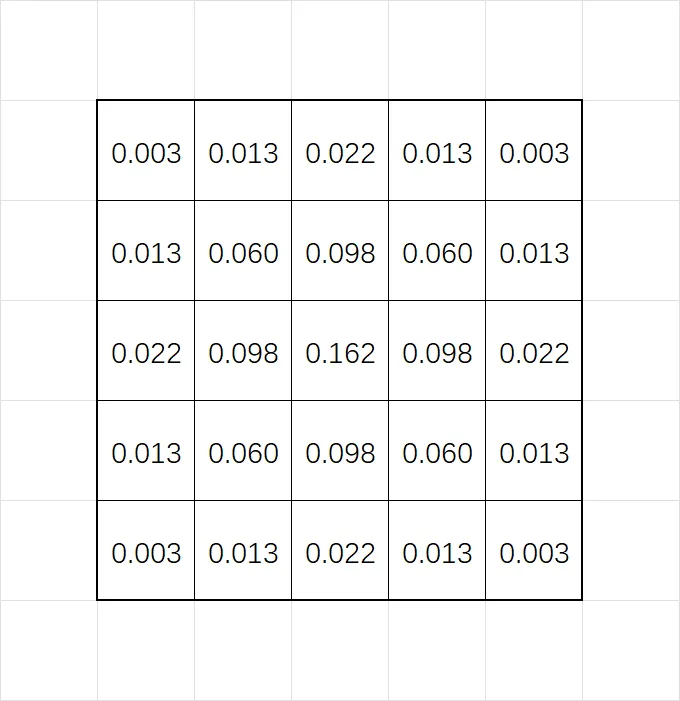
除了平均，卷积核还能求导：

中间是 $2$ 只是一个优化，如果不能理解，就把它当作 $1$ 来看。

上面均讨论的二维离散卷积，3b1b 的视频分享了一个很有趣的一维离散卷积的一种现实中的意义，感兴趣可以观看：https://www.bilibili.com/video/BV1Vd4y1e7pj

通过构造不同的卷积核，卷积操作可以被赋予不同意义，实现不同功能。例如是可以通过构造一个卷积核来实现提取图片某个特征的。

因此，我们只需要了解卷积是一种运算，一种结合两个函数形成新函数的方法就行了。具体卷积核实现的不同功能，就得在实践中积累学习了。

3 卷积和互相关

大家可能已经感觉到，计算中途将卷积核翻转 $180^{\circ}$ 的操作莫名其妙，完全没理由，其实它确实没理由，因为卷积就是这样定义的。不翻转卷积核进行上述运算，那么这个操作在数学中被定义为互相关 (Correlation).

我们没有必要纠结为啥这样定义，这就像为什么加法是这样，乘法是这样一样，这就是定义，没有理由，记住就行。

在数学语境中，需要注意卷积和互相关的区别。在计算机科学领域中就无需纠结了，你大可以图方便不翻转，平时我们说卷积时也不关心翻不翻转。