快速的字符串匹配算法（在主串中匹配模式串）：KMP 算法 (The Knuth-Morris-Pratt Algorithm)

KMP 算法

复杂度

时间复杂度：$O(n+m)$

空间复杂度：$O(m)$

（$n$ 为主串长度，$m$ 为模式串长度）

分析

KMP 算法的核心为部分匹配表，一般称 Next 数组。

部分匹配表

部分匹配表 (PMT, Partial Match Table)

直接按概念解释的话，PMT 中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。

举个例子，以字符串 $ABABA$ 为例，
该字符串的前缀集合为：$\big\{\{A\},\{AB\},\{ABA\},\{ABAB\}\big\}$
该字符串的后缀集合为：$\big\{\{BABA\},\{ABA\},\{BA\},\{A\}\big\}$

注意，前缀集合和后缀集合不能包含自己（自身肯定等于自身，这样比较就无意义了）

该字符串前缀集合与后缀集合的交集：$\big\{\{A\},\{ABA\}\big\}$
交集中的最长元素：$\{ABA\}$
最长元素的长度：$3$

容易理解的方式来说就是：字符串 前 $k$ 个字符 = 后 $k$ 个字符，如上述例子，前 $3$ 个字符为 $ABA$，后 $3$ 个字符为 $ABA$

下图具体举了一个 PMT 表的例子，以字符串 $ABCABACA$ 为例

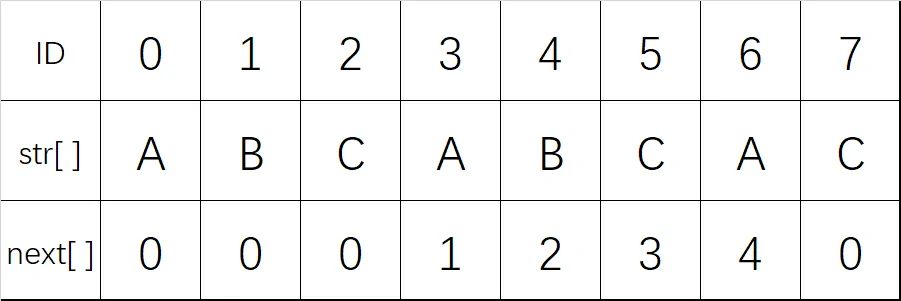
至于这个表怎么求，先放一下。得先了解 KMP 算法才好理解，因为这俩玩意互相交叉，联系很紧密。

KMP 算法主体

下面以主串 $ABCABCD\cdots$，模式串 $ABCABB$ 为例。

因为 KMP 算法就是从暴力解法优化而来的，我们先看暴力解法：

从第一位开始，一个个向后比对，直到失配为止：

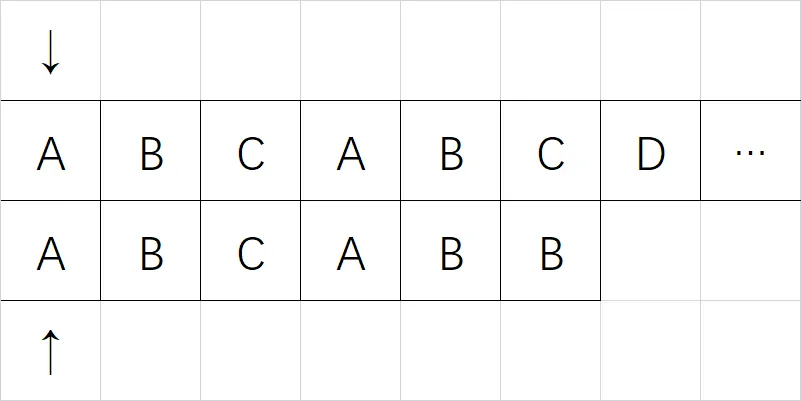
可以看到数组下标为 5 的时候，没能成功匹配上：

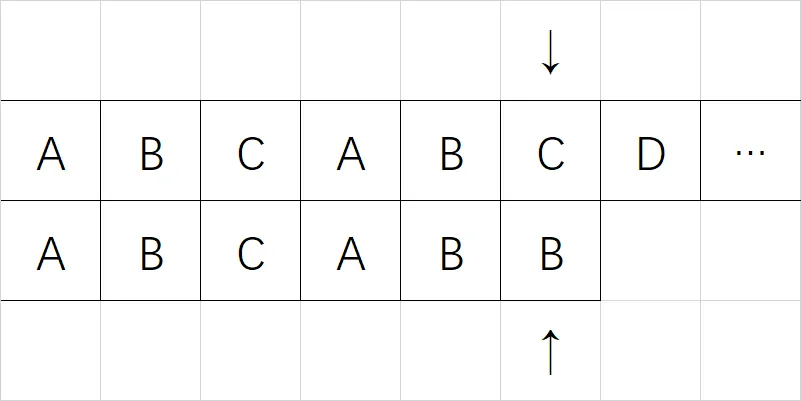
这时，暴力解法就会将模式串右移一位，再来从头比较一遍，直到失配为止，然后再来循环……：

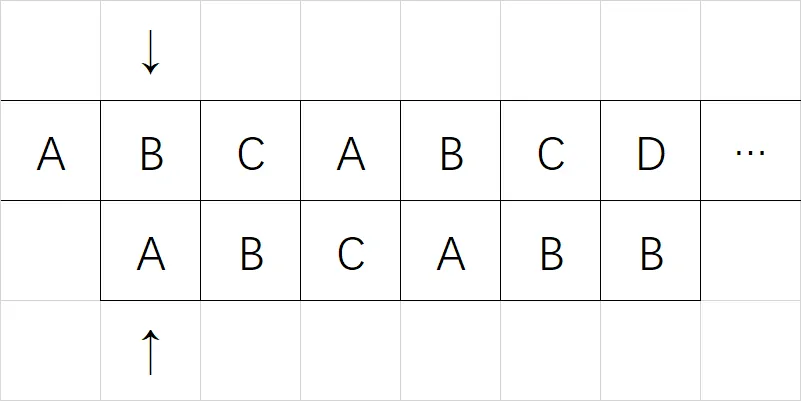
可以看到，暴力解法将每一位主串和每一位模式串进行了比对，非常耗时。

失配后，真的要从头再比对一遍吗？

观察这个失配的情况，可以发现，数组的 0~4 位，其实已经匹配过了，我们能保证这四位是一样的。那像暴力解法，把模式串错开一位，不用想肯定是一位都匹配不上的，包括错开两位、错开三位其实也都是肯定配不上的。

那能不能直接知道，失配后应该将模式串移动几位呢？这时 PMT 表就用到了，下面是模式串的 PMT 表：

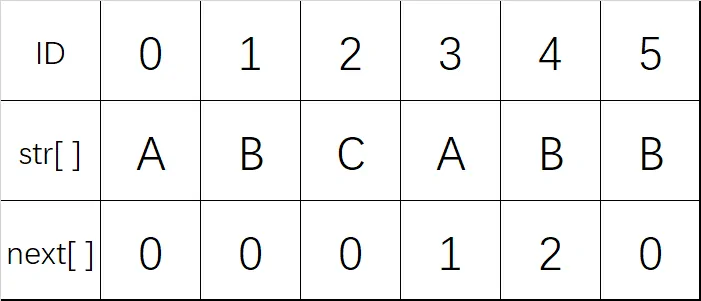
刚才我们在第 5 位失配，往前看一位，模式串第四位的 PMT 表值为 2，意思是 0~1 位和 3~4 位一样，我们还知道什么？还知道模式串 0~4 位都能和主串匹配。那我们完全可以把模式串以前 0~1 的元素位置挪到以前 3~4 位元素的位置，仍然能够保证与主串匹配，如下图：

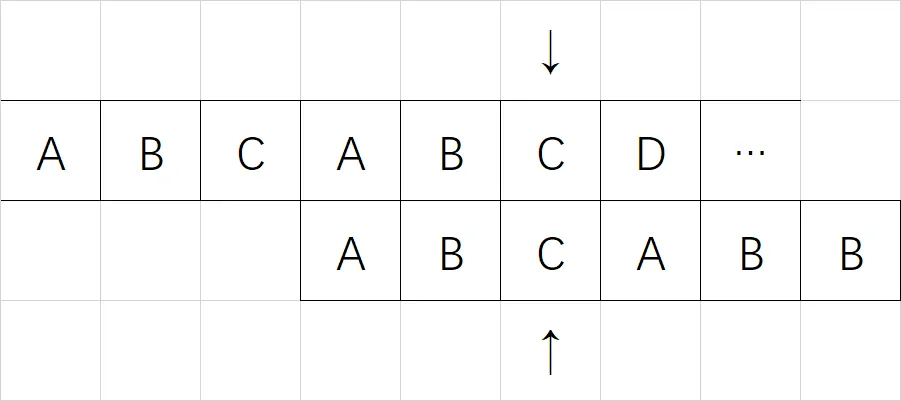
最重要的一点，我们能知道挪动过后的模式串 0~1 位绝对能和主串匹配，那么我们就不需要再从头匹配，甚至指针都不需要挪动，就可以继续匹配了，这便是 KMP 算法的精髓所在，主串指针不需要反复横跳，而是只会从头到尾走一遍，因此可知时间复杂度 $O(m)$

当然，如果移动后仍然失配，那就得再次移动，直到又成从头开始匹配的情况。

通过 KMP 算法的思想求出部分匹配表（next 数组）

实际上，求 next 数组就是一次 KMP 算法，只不过是模式串和它自己匹配。

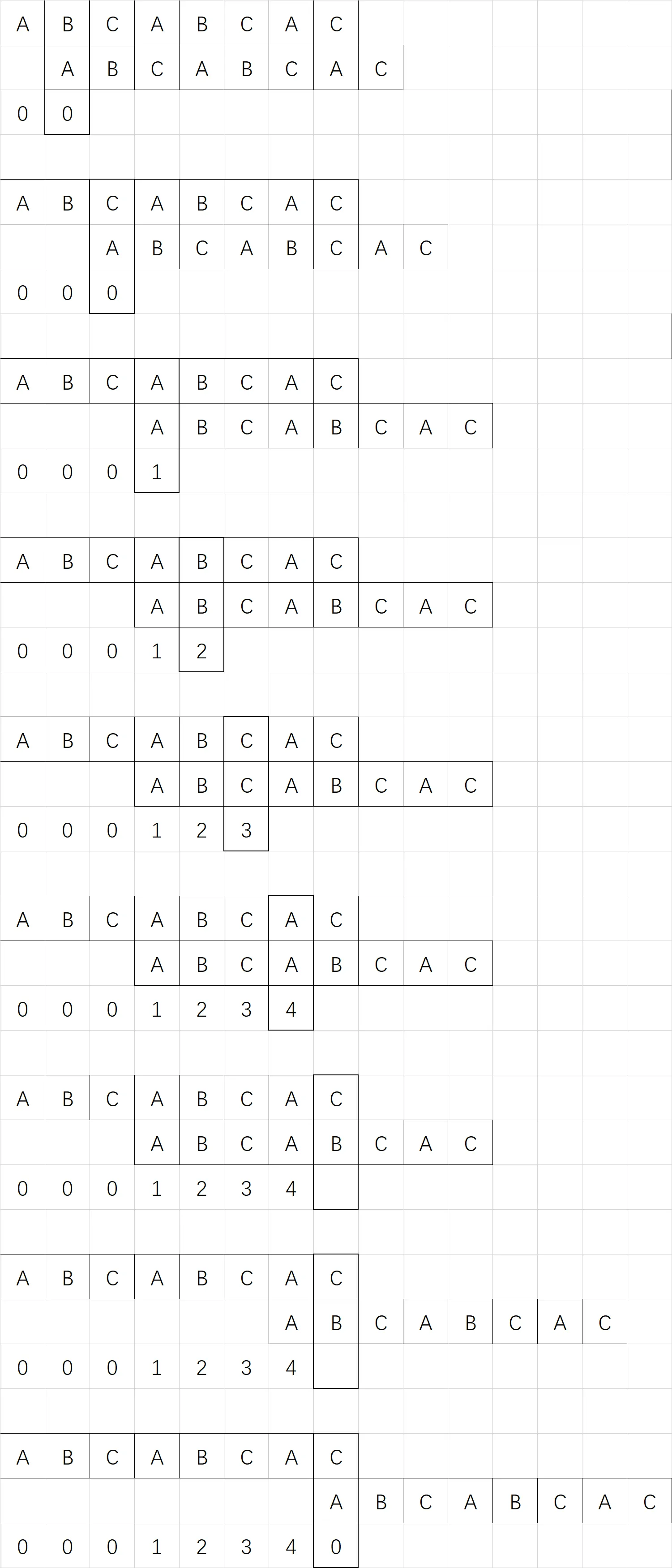
可以看下图，首先 next[0] 直接初始化为 0，然后从第一位开始比对。如果失配就挪动下面的模式串，如果挪到头还没匹配上就填 0，如果匹配上就 +1.

同理，时间复杂度就为 $O(n)$，那么 KMP 算法的总时间复杂度就为 $O(m+n)$

代码实现

计算部分匹配表

char s1[MAXN]; // 主串
char s2[MAXN]; // 模式串
int nxt[MAXN]; // 部分匹配表
void getnext(void)
{
    nxt[0] = -1;
    int i = 0, j = -1;
    int lens2 = strlen(s2);
    while (i < lens2)
    {
        if (j == -1 || s2[i] == s2[j])
        {
            ++i;
            ++j;
            nxt[i] = j;
        }
        else
        {
            j = nxt[j];
        }
    }
}

需要注意，代码中的 nxt 数组和上面分析的有所不同，其下标都增大了一位，且 nxt[0] = -1，这样做是为了方便编程，因为 -1 + 1 后为零，起到了模式串从头开始匹配的作用。上下两个代码是配套的，如果上面不用 -1 这种设计的话，下面的 KMP 算法也需要修改。

下面是本文代码的 nxt 数组的样子，可以看到数组需要多开一位（不过一般写题都会多开十几位，正好用上）

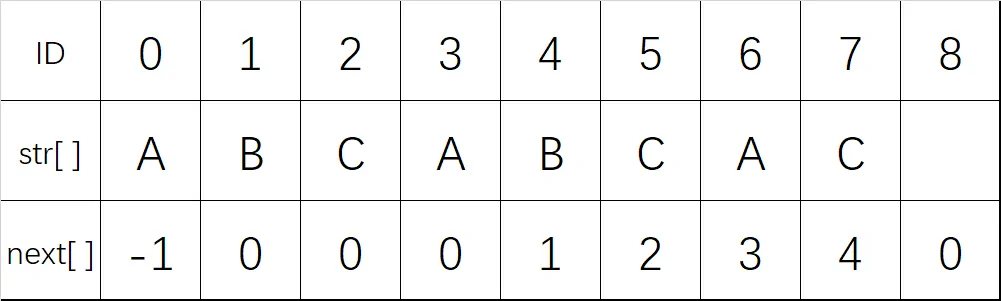
KMP 算法

char s1[MAXN]; // 主串
char s2[MAXN]; // 模式串
int nxt[MAXN]; // 部分匹配表
void kmp(void)
{
    int i = 0, j = 0;
    int lens1 = strlen(s1), lens2 = strlen(s2);
    while (i < lens1)
    {
        if (j == -1 || s1[i] == s2[j])
        {
            i++;
            j++;
        }
        else
        {
            j = nxt[j];
        }
        if (j == lens2)
        {
            printf("%d\n", i - j + 1);
        }
    }
}

如果说只需要匹配一个结果就行，那么就改为以下写法

char s1[MAXN]; // 主串
char s2[MAXN]; // 模式串
int nxt[MAXN]; // 部分匹配表
void kmp(void)
{
    int i = 0, j = 0;
    int lens1 = strlen(s1), lens2 = strlen(s2);
    while (i < lens1 && j < lens2)
    {
        if (j == -1 || s1[i] == s2[j])
        {
            i++;
            j++;
        }
        else
        {
            j = nxt[j];
        }
    }
    if (j == lens2)
    {
        printf("%d\n", i - j + 1);
    }
    else
    {
        printf("-1\n"); // -1表示没匹配到结果
    }
}

类封装实现

使用时先调用构造函数构造 KMP 类，需要向其中传入模式串，匹配时调用 .find()，传入主串。

class KMP
{
    vector<int> nxt;
    string pat;

public:
    KMP(string &s)
    {
        pat = s;
        int n = pat.length();
        int j = 0;
        nxt.resize(n);
        for (int i = 1; i < n; i++)
        {
            while (j > 0 && pat[i] != pat[j])
                j = nxt[j - 1];
            if (pat[i] == pat[j])
                j++;
            nxt[i] = j;
        }
    }
    vector<int> find(string &txt)
    {
        int n = pat.length(), m = txt.length();
        int j = 0;
        vector<int> ans;
        for (int i = 0; i < m; i++)
        {
            while (j > 0 && txt[i] != pat[j])
                j = nxt[j - 1];
            if (txt[i] == pat[j])
                j++;
            if (j == n)
            {
                ans.push_back(i - n + 1);
                j = nxt[j - 1];
            }
        }
        return ans;
    }
    set<int> get_border()
    {
        set<int> s;
        int cur = nxt.back();
        while (cur)
        {
            s.insert(cur);
            cur = nxt[cur - 1];
        }
        s.insert(0);
        return s;
    }
};