题目 | Subtree K-th Max

Denso Create Programming Contest 2022(AtCoder Beginner Contest 239)

E - Subtree K-th Max

https://atcoder.jp/contests/abc239/tasks/abc239_e

Time Limit: 2 sec / Memory Limit: 1024 MB

Score : $500$ points

Problem Statement

We have a rooted tree with $N$ vertices. The vertices are numbered $1$ through $N$ , and the root is Vertex $1$ .
The $i$ -th edge connects Vertices $A_{i}$ and $B_{i}$ .
Vertex $i$ has an integer $X_{i}$ written on it.

You are given $Q$ queries. For the $i$ -th query, given a pair of integers $(V_{i}, K_{i})$ , answer the following question.

Question: among the integers written on the vertices in the subtree rooted at Vertex $V_{i}$ , find the $K_{i}$ -th largest value.

Constraints

$2 \leq N \leq 10^{5}$
$0 \leq X_{i} \leq 10^{9}$
$1 \leq A_{i}, B_{i} \leq N$
$1 \leq Q \leq 10^{5}$
$1 \leq V_{i} \leq N$
$1 \leq K_{i} \leq 20$
The given graph is a tree.
The subtree rooted at Vertex $V_{i}$ has $K_{i}$ or more vertices.
All values in input are integers.

Input

Input is given from Standard Input in the following format:

$N$ $Q$
$X_{1}$ $\dots$ $X_{N}$
$A_{1}$ $B_{1}$
$⋮$
$A_{N - 1}$ $B_{N - 1}$
$V_{1}$ $K_{1}$
$⋮$
$V_{Q}$ $K_{Q}$

Output

Print $Q$ lines. The $i$ -th line should contain the response to the $i$ -th query.

Sample Input 1

5 2
1 2 3 4 5
1 4
2 1
2 5
3 2
1 2
2 1

Sample Output 1

4
5

The tree given in this input is shown below.

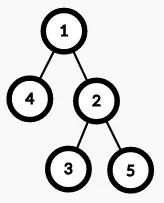
For the $1$ -st query, the vertices in the subtree rooted at Vertex $1$ are Vertices $1, 2, 3, 4$ , and $5$ , so print the $2$ -nd largest value of the numbers written on these vertices, $4$ .
For the $2$ -nd query, the vertices in the subtree rooted at Vertex $2$ are Vertices $2, 3$ , and $5$ , so print the $1$ -st largest value of the numbers written on these vertices, $5$ .

Sample Input 2

6 2
10 10 10 9 8 8
1 4
2 1
2 5
3 2
6 4
1 4
2 2

Sample Output 2

9
10

Sample Input 3

4 4
1 10 100 1000
1 2
2 3
3 4
1 4
2 3
3 2
4 1

Sample Output 3

1
10
100
1000

我的笔记

核心思路就是预计算出每一个节点的前 $20$ 大的值，然后储存到 vector<int> max_20_value[node] 里，最后直接输出对应第 $K_{i}$ 大的值即 max_20_value[N][max_20_value[N].size() - Q]。

具体做法是先建树，储存每个节点的子节点和父节点。 $1$ 为根节点，因此得手动设置它的父节点为 $1$ ，否则建树时根节点就混乱了。

然后用 DFS，每一个节点的操作：先将它的所有子节点的 max_20_value[subnode] 的值全部添加到自身的 max_20_value[node] 内，然后排序，如果值的数量 $> 20$ ，就循环删除最小的值直到数量 $= 20$ ，这样就得到了前 $20$ 大的值的列表。

因为 DFS 每一层都需要用到下一层的结果，所以得先递归到底然后再进行操作。对应到代码就是每一层先 DFS，再进行其他操作。

代码

#include <bits/stdc++.h>
#define SIZE 100010

using namespace std;

vector<int> max_20_value[SIZE];
vector<int> link[SIZE];
int father[SIZE] = {0, 1};
vector<int> son[SIZE];

void creat_tree(int x)
{
    for (auto i : link[x])
    {
        if (father[i])
            continue;
        father[i] = x;
        son[x].push_back(i);
        creat_tree(i);
    }
}

void calc_max_20_value(int x)
{
    for (auto i : son[x])
    {
        calc_max_20_value(i);
        for (auto j : max_20_value[i])
        {
            max_20_value[x].push_back(j);
        }
    }
    sort(max_20_value[x].begin(), max_20_value[x].end());
    while (max_20_value[x].size() > 20)
    {
        max_20_value[x].erase(max_20_value[x].begin());
    }
}

int main(void)
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int N, Q;
    cin >> N >> Q;
    for (int i = 1; i <= N; i++)
    {
        int X;
        cin >> X;
        max_20_value[i].push_back(X);
    }
    for (int i = 1; i < N; i++)
    {
        int A, B;
        cin >> A >> B;
        link[A].push_back(B);
        link[B].push_back(A);
    }
    creat_tree(1);
    calc_max_20_value(1);
    for (int i = 1; i <= Q; i++)
    {
        int N, Q;
        cin >> N >> Q;
        cout << max_20_value[N][max_20_value[N].size() - Q] << endl;
    }
    return 0;
}