二分图又称作二部图，是图论中的一种特殊模型。 设 $G=(V,E)$ 是一个无向图，如果顶点 $V$ 可分割为两个互不相交的子集 $(A,B)$，并且图中的每条边 $(i,j)$ 所关联的两个顶点 $i$ 和 $j$ 分别属于这两个不同的顶点集 $(i\in A,j\in B)$，则称图 $G$ 为一个二分图。

染色法判别二分图

如下图，用红和绿（实际用 0 和 1 表示）对这个图染色，相邻的顶点不可染相同颜色，那么就能得到以下情况：

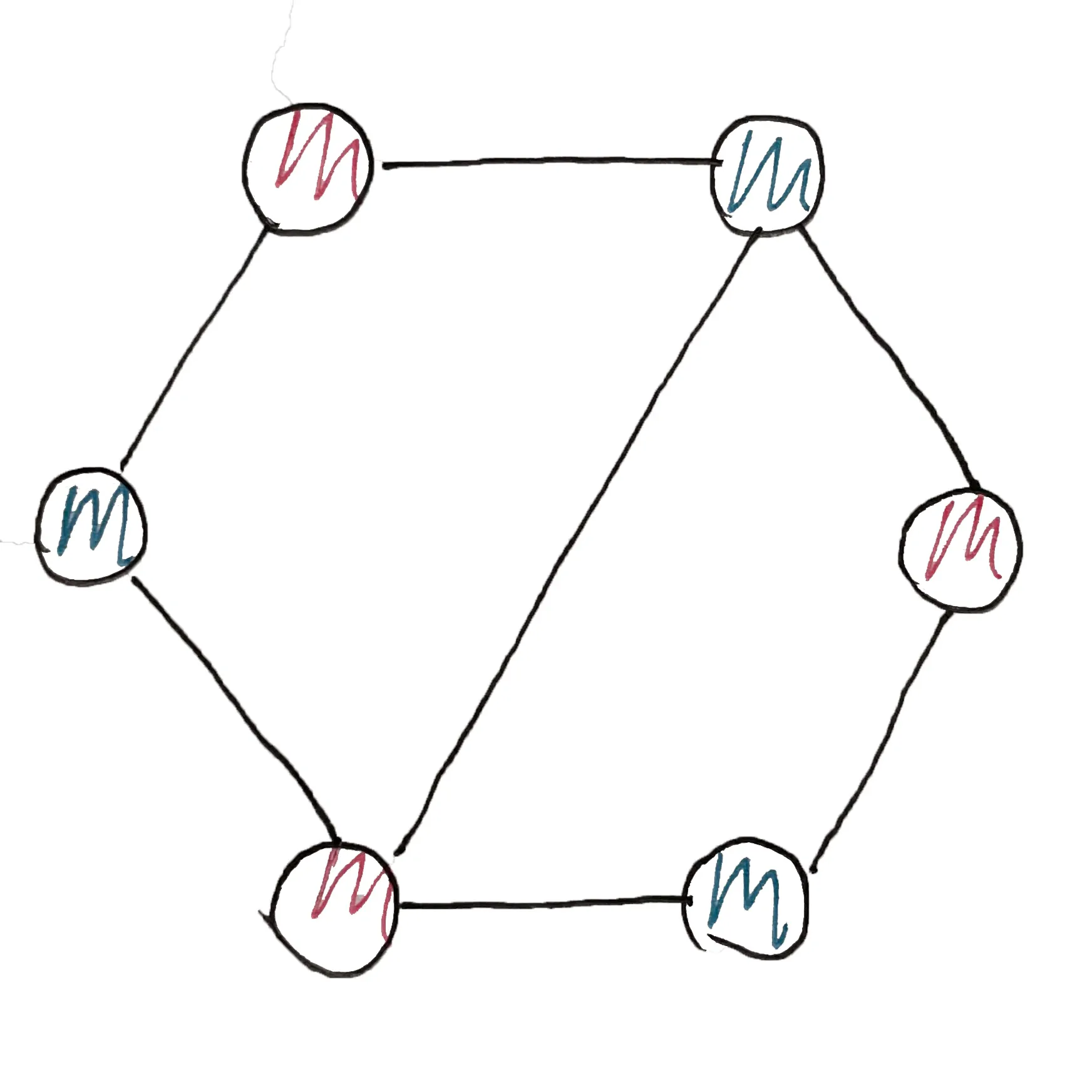
如果能将一个图无矛盾地染色，那么这就是一个二分图，将同色顶点放到一起，就将这个图一分为二，这便是染色法判别二分图的思想。

由此也能得到二分图的一个性质：不存在奇环。如果存在奇环，那么染色时一定会出现矛盾，不是二分图。（无环也是二分图）

复杂度

时间复杂度：$O(\left|V\right|+\left|E\right|)$

$\left|E\right|$ 为边数，$\left|V\right|$ 为顶点数。

代码实现

染色过程即对图进行了一次遍历，可用 DFS 实现，每层 DFS 染不同颜色即可。

连通图

const int SIZE = 1e5 + 10;
int V, E;                   // V为顶点，E为边
vector<int> edge[SIZE];     // vector邻接表，可改为数组邻接表效率更高
int color[SIZE];            // 储存颜色，用0和1表示两种颜色，-1表示还未染色。重要：使用前先memset为-1
/* vector<int> ans[2]; */   // 储存两颜色的顶点，某些题目需要输出

bool dfs(int n, int c)
{
    color[n] = c;
    /* ans[colr].push_back(node); */   // 储存两颜色的顶点，某些题目需要输出
    for (auto nxt : edge[n])
    {
        if (color[n] == -1)
        {
            if (!dfs(nxt, !c))
                return false;
        }
        else if (color[nxt] == c)
        {
            return false;
        }
    }
    return true;
}

非连通图

若图并不联通，那么一次查找还不够。因为一个图如果是二分图，需要每个连通分支都是二分图，整个图才是二分图。

因此需要从点 $1$ 遍历到点 $V$，如果一个点还未染色，说明它没有联通，需要从这个点再染一边色。因此需要额外的以下代码在主函数内。

bool flag = true;
for (int i = 1; i <= V; i++)
{
    if (color[i] == -1)
    {
        if (!dfs(i, 0))
        {
            flag = false;
            break;
        }
    }
}

求二分图最大匹配

定义

二分图的匹配：给定一个二分图 $G$，在 $G$ 的一个子图 $M$ 中，$M$ 的边集 $\{E\}$ 中的任意两条边都不依附于同一个顶点，则称 $M$ 是一个匹配。

二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。

解释这个最大匹配，经常用男女配对来打比方（笑

如下图，易得这是一个二分图。可以把左边一列看为男生，右边一列看为女生，我们要求能够匹配上的男生女生的最大数目。当然，“海王”行为是不可取的，一个男生只能和一个女生匹配，反正同理。

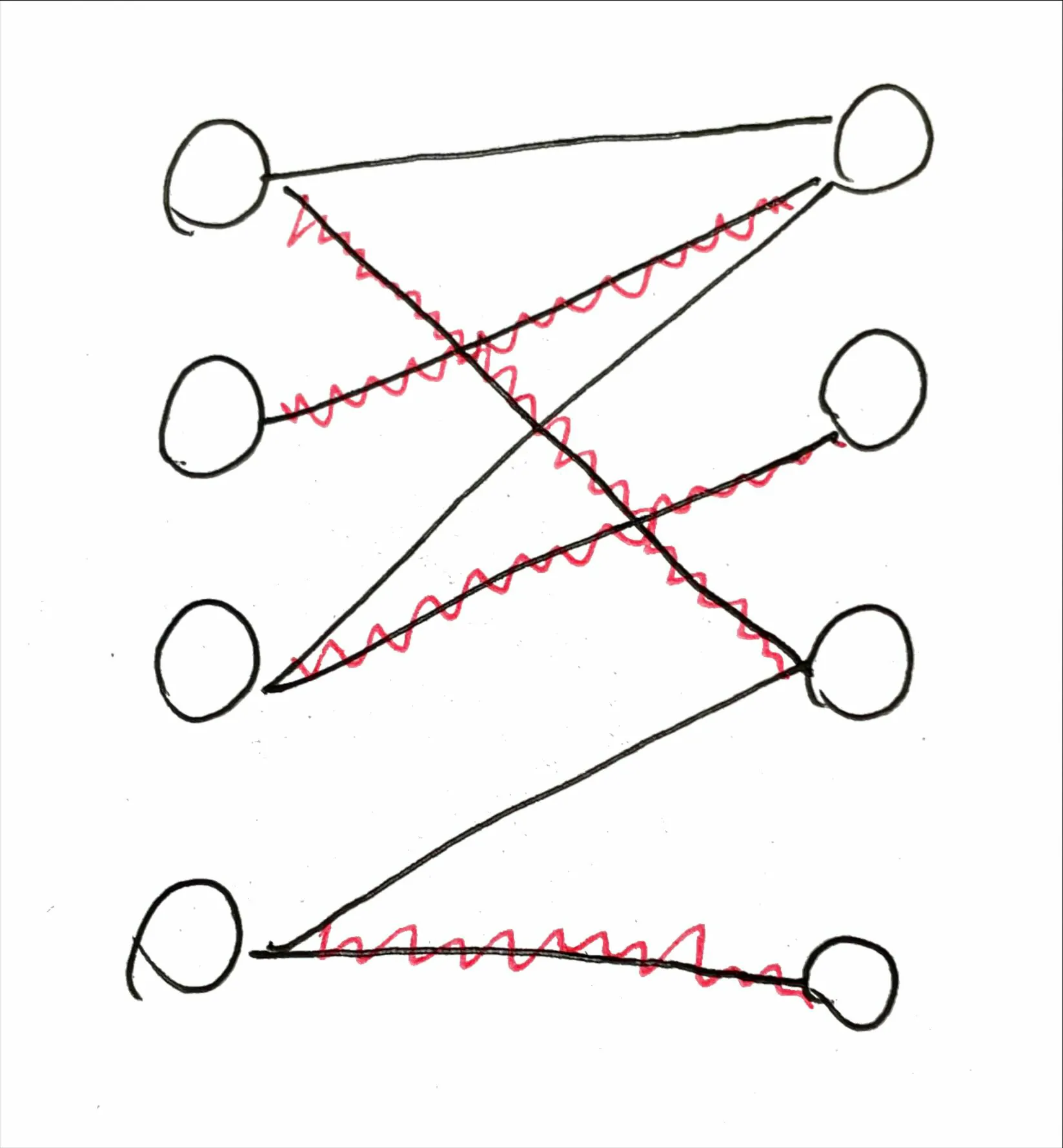
匈牙利算法 (Hungarian Algorithm)

复杂度

时间复杂度：$O(\left|V\right|\cdot \left|E\right|)$

$\left|E\right|$ 为边数，$\left|V\right|$ 为顶点数。一般情况的时间复杂度会远小于该理论值。

算法过程

就以上图为例，编一个号方便讲解。左侧的子图四个顶点记为 $B_1,B_2,B_3,B_4$，右侧的子图四个顶点记为 $G_1,G_2,G_3,G_4$。

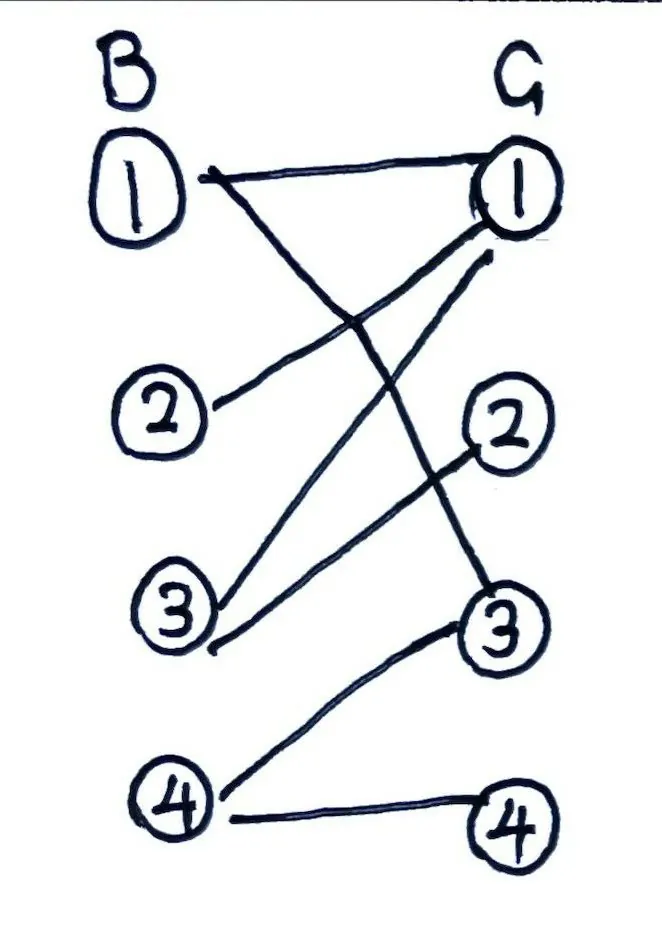
尝试给 $B_1$ 匹配女生：

$B_1$ 对 $G_1,G_3$ 有好感。

尝试与 $G_1$ 匹配，此时 $G_1$ 还单身，因此顺利匹配成功。

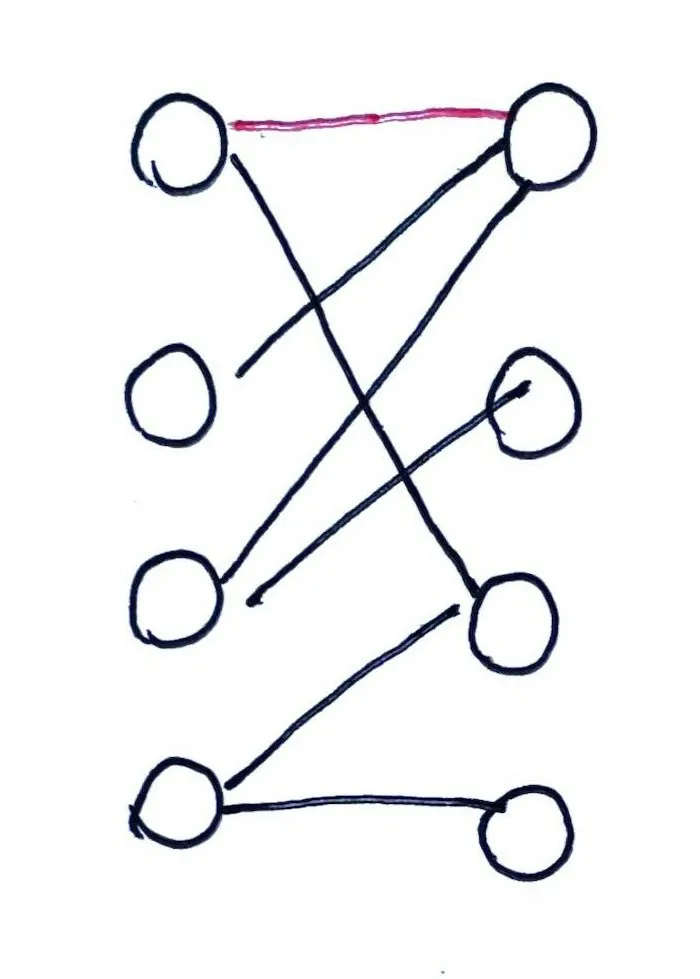
尝试给 $B_2$ 匹配女生：

$B_2$ 对 $G_1$ 有好感。

尝试与 $G_1$ 匹配，此时 $G_1$ 已经匹配了 $B_1$，尝试让 $B_1$ 更换匹配的女生。

$B_1$ 可更换为与 $G_3$ 匹配，然后 $B_2$ 就能成功与 $G_1$ 匹配。

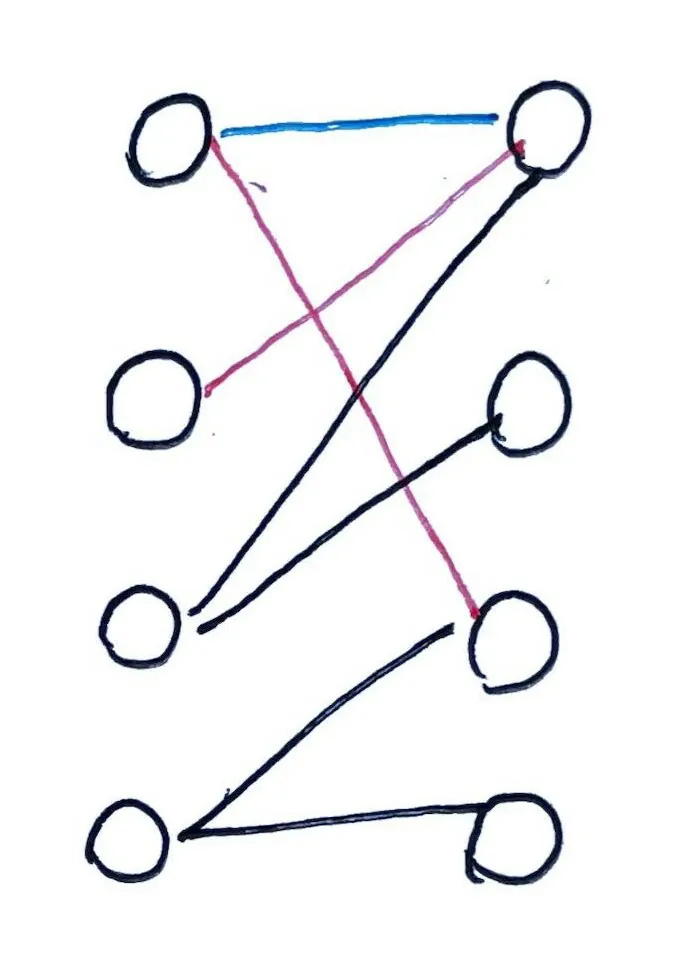
尝试给 $B_3$ 匹配女生：

$B_3$ 对 $G_1,G_2$ 有好感。

尝试与 $G_1$ 匹配，此时 $G_1$ 已经匹配了 $B_2$，尝试让 $B_2$ 更换匹配的女生。

$B_2$ 没有可更换匹配的女生，因此 $B_2$ 无法与 $G_1$ 匹配。

尝试与 $G_2$ 匹配，此时 $G_2$ 还单身，因此顺利匹配成功。

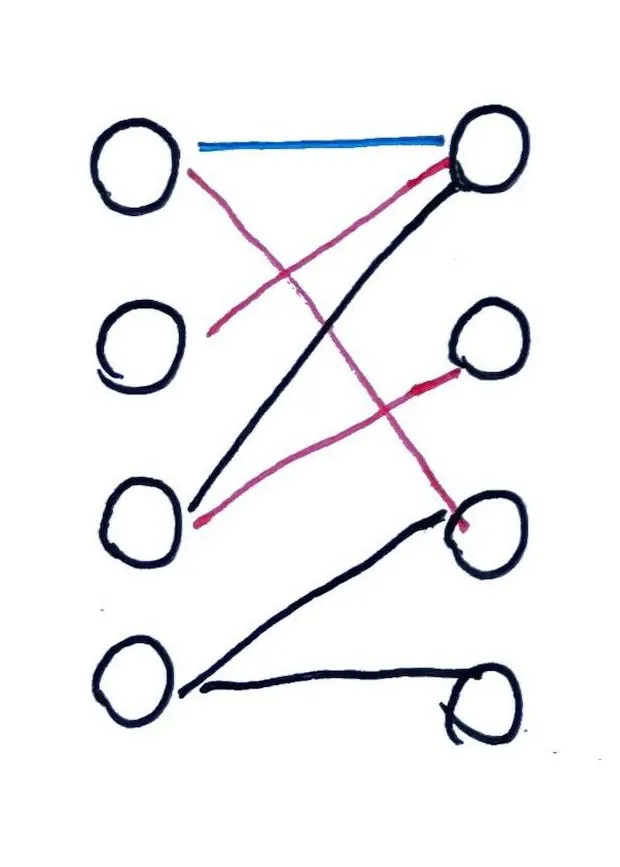
尝试给 $B_4$ 匹配女生：

$B_4$ 对 $G_3,G_4$ 有好感。

尝试与 $G_3$ 匹配，此时 $G_3$ 已经匹配了 $B_1$，尝试让 $B_1$ 更换匹配的女生。

$B_1$ 没有可更换匹配的女生，因此 $B_4$ 无法与 $G_3$ 匹配。

尝试与 $G_4$ 匹配，此时 $G_4$ 还单身，因此顺利匹配成功。

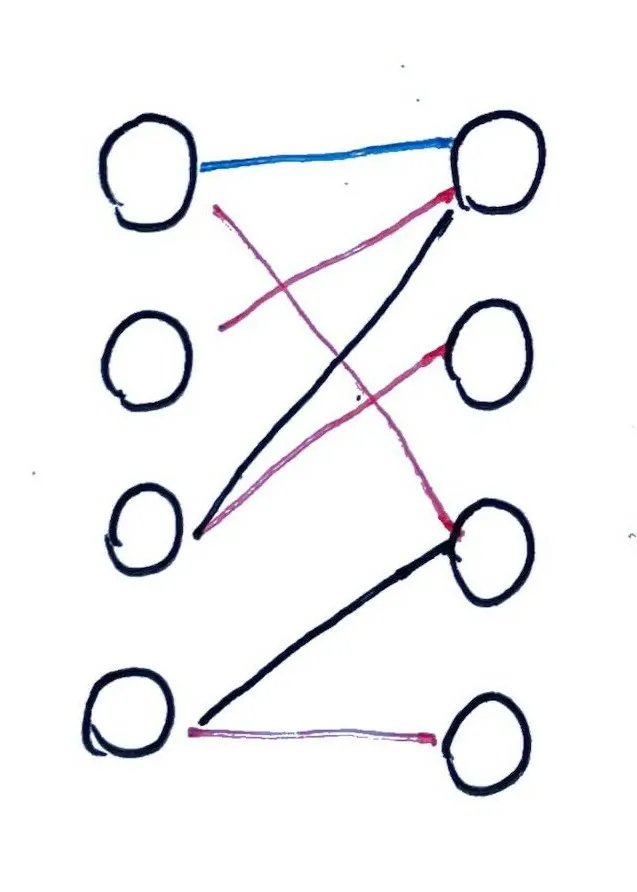
匹配完成，最大匹配数：4

代码实现

#include <bits/stdc++.h>

using namespace std;

const int SIZE = 1010;

int n1, n2, m;          // n1为二分图的一个子图的顶点数，n2为另一个子图的顶点数，m为边数。
vector<int> edge[SIZE]; // 这里使用vector存图
int match[SIZE];        // 储存n2中的某个顶点匹配的n1中的顶点
bool vis[SIZE];         // 标记n2中的某个顶点是否已经匹配过

bool find(int x)
{
    // 遍历所有与x连接的n2内的顶点i
    for (auto i : edge[x])
    {
        // 如果顶点i本轮还未匹配过
        if (!vis[i])
        {
            // 将其标记
            vis[i] = true;
            // 若顶点i还没有匹配到任何n1中顶点，则直接把i与x匹配
            // 如果i已经匹配上，则查询与i匹配的n1中的元素能否换一个匹配，若可以，则将i与x匹配
            if (match[i] == 0 || find(match[i]))
            {
                match[i] = x;
                return true;
            }
        }
    }
    // 如果没法匹配上，返回false
    return false;
}

int main(void)
{
    cin >> n1 >> n2 >> m;
    for (int i = 0; i < m; i++)
    {
        int u, v;
        cin >> u >> v;
        // 只用得到从n1到n2的边，因此只存了单向边
        edge[u].push_back(v);
    }
    int cnt = 0; // 匹配的数量
    // 从n1第一个元素开始，尝试匹配到最后一个元素
    for (int i = 1; i <= n1; i++)
    {
        // 先清空所有n2的访问情况
        memset(vis, false, sizeof(vis));
        // 如果匹配上则匹配数+1
        if (find(i))
            cnt++;
    }
    cout << cnt << endl;
    return 0;
}