题目 | Keep Connect - 颢天笔记

UNIQUE VISION Programming Contest 2022（AtCoder Beginner Contest 248）

F - Keep Connect

https://atcoder.jp/contests/abc248/tasks/abc248_f

Time Limit: 2 sec / Memory Limit: 1024 MB

Score : $500$ points

Problem Statement

You are given an integer $N$ greater than or equal to $2$ and a prime $P$.
Consider the graph $G$ with $2N$ vertices and $(3N-2)$ edges shown in the figure below.

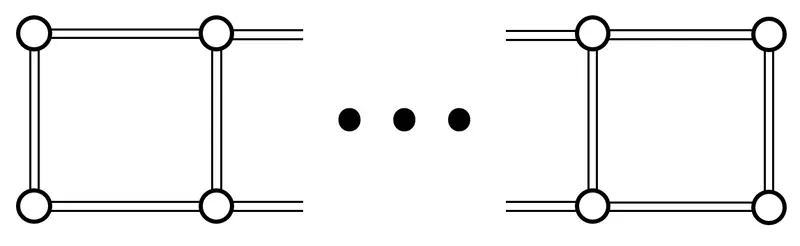
More specifically, the edges connect the vertices as follows, where the vertices are labeled as Vertex $1$, Vertex $2$, $\ldots$, Vertex $2N$, and the edges are labeled as Edge $1$, Edge $2$, $\ldots$, Edge $(3N-2)$.

For each $1\leq i\leq N-1$, Edge $i$ connects Vertex $i$ and Vertex $i+1$.
For each $1\leq i\leq N-1$, Edge $(N-1+i)$ connects Vertex $N+i$ and Vertex $N+i+1$.
For each $1\leq i\leq N$, Edge $(2N-2+i)$ connects Vertex $i$ and Vertex $N+i$.

For each $i=1,2,\ldots ,N-1$, solve the following problem.

Find the number of ways, modulo $P$, to remove exactly $i$ of the $3N-2$ edges of $G$ so that the resulting graph is still connected.

Constraints

$2 \leq N \leq 3000$
$9\times 10^8 \leq P \leq 10^9$
$N$ is an integer.
$P$ is a prime.

Input

Input is given from Standard Input in the following format:

$N$ $P$

Output

Print $N-1$ integers, the $i$-th of which is the answer for $i=k$, separated by spaces.

Sample Input 1

3 998244353

Sample Output 1

7 15

In the case $N=3$, there are $7$ ways, shown below, to remove exactly one edge so that the resulting graph is still connected.

There are $15$ ways, shown below, to remove exactly two edges so that the resulting graph is still connected.

Thus, these numbers modulo $P=998244353$ should be printed: $7$ and $15$, in this order.

Sample Input 2

16 999999937

Sample Output 2

46 1016 14288 143044 1079816 6349672 29622112 110569766 330377828 784245480 453609503 38603306 44981526 314279703 408855776

Be sure to print the numbers modulo $P$.

我的笔记

首先将这个图的边 $E$ 分成三种：

$E_{a_1},E_{a_2},\dots,E_{a_{N-1}}$，即顶部的边，编号 $i=1,2,\dots,N-1$，如下图红边；
$E_{b_1},E_{b_2},\dots,E_{b_{N-1}}$，即底部的边，编号 $i=1,2,\dots,N-1$，如下图蓝边；
$E_{c_0},E_{c_1},\dots,E_{c_{N-1}}$，即中间的边，编号 $i=0,1,\dots,N-1$，如下图绿边。

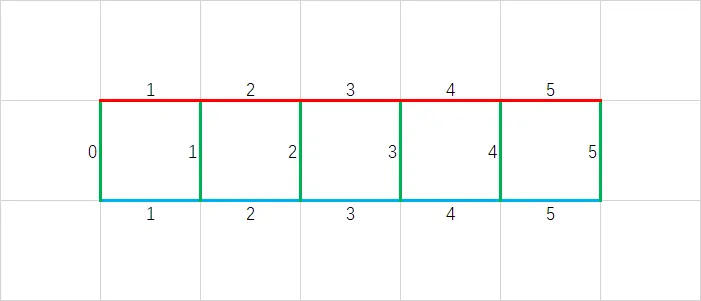
然后把这个图的顶点 $V$ 分成两种：

$V_{a_0},V_{a_1},\dots,V_{a_{N-1}}$，即上面的一排点；
$V_{b_0},V_{b_1},\dots,V_{b_{N-1}}$，即下面的一排点。

定义图 $G_i$：包含边 $E_{a_1},E_{a_2},\dots,E_{a_i}$、$E_{b_1},E_{b_2},\dots,E_{b_{i}}$、$E_{c_0},E_{c_1},\dots,E_{c_{i}}$，包含点 $V_{a_0},V_{a_1},\dots,V_{a_i}$、$V_{b_0},V_{b_1},\dots,V_{b_i}$。

将图 $G_i$ 的状态分成两种：

状态 $0$：图联通，如下图中上侧图。
状态 $1$：图不连通，但有两个联通子图，并且两子图分别包含 $V_{a_i}$、$V_{b_i}$，如下图中下侧图。

然后运用动态规划思想，$dp[i][j][k]:=$ 在子图 $G_i $中，去除 $j$ 条边后，处于状态 $k$ 的图的数量。

首先初始化 $dp$ 数组，$G_0$ 只有一条边 $E_{c_0}$，要么去要么不去，因此 $dp[0][0][0]=1$，$dp[0][1][1]=1$。

然后寻找递推方法，先思考 $dp[i-1][j][1]$ 的情况：

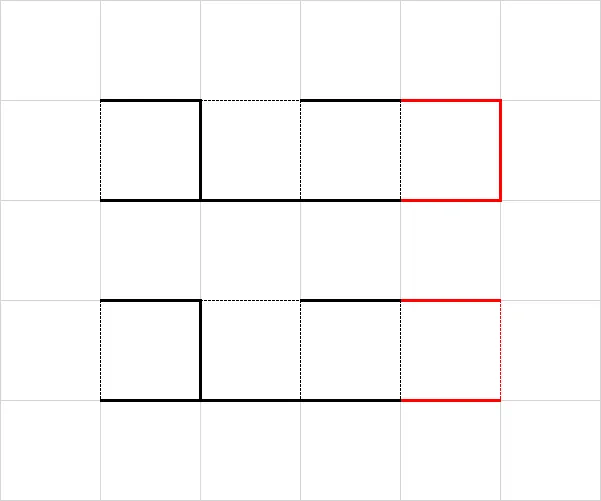
如果新加的三条边 $E_{a_i},E_{b_i},E_{c_i}$ 都保留，那么这个图会变成状态 $0$，如下图上面的情况（红色为新加的边）
- 递推式：$dp[i][j][0]$ += $dp[i-1][j][1]$
如果新加的三条边 $E_{a_i},E_{b_i},E_{c_i}$ 去掉 $E_{c_i}$，那么这个图仍然为状态 $1$，如下图下面的情况
- 递推式：$dp[i][j+1][1]$ += $dp[i-1][j][1]$

再考虑 $dp[i-1][j][0]$ 的情况：

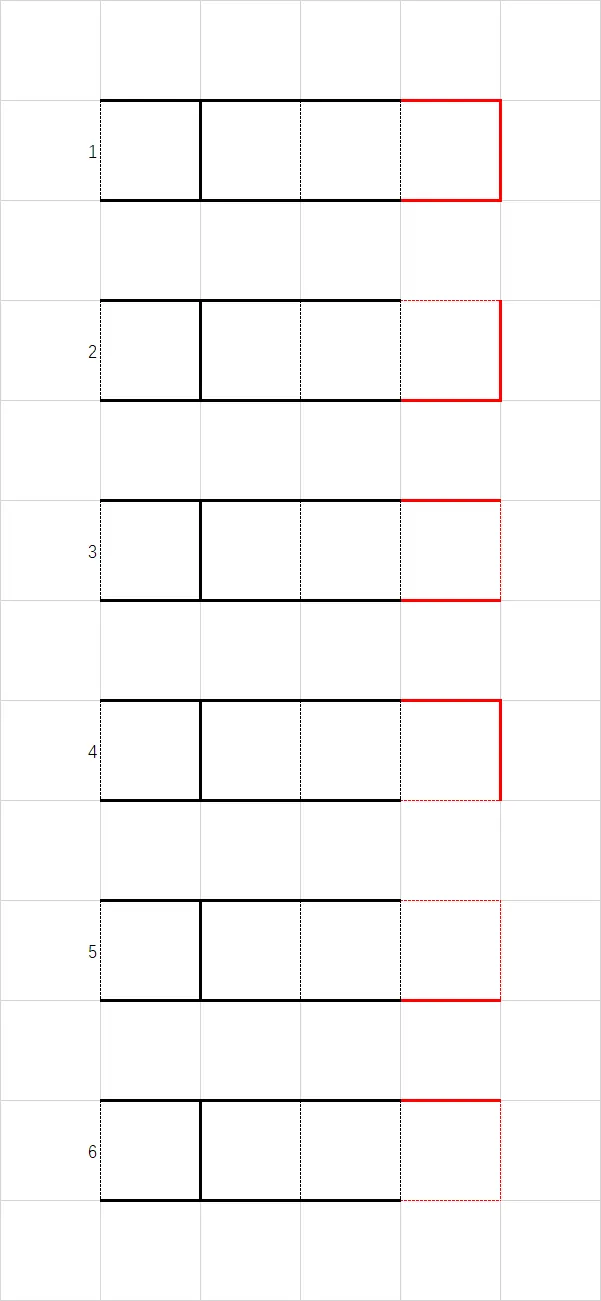
如果新加的三条边 $E_{a_i},E_{b_i},E_{c_i}$ 都保留，那么这个图仍然为状态 $0$，如下图 $1$ 号情况（红色为新加的边）
- 递推式：$dp[i][j][0]$ += $dp[i-1][j][0]$
如果新加的三条边 $E_{a_i},E_{b_i},E_{c_i}$ 去掉 $E_{a_i}$，那么这个图仍然为状态 $0$，如下图 $2$ 号情况
如果新加的三条边 $E_{a_i},E_{b_i},E_{c_i}$ 去掉 $E_{c_i}$，那么这个图仍然为状态 $0$，如下图 $3$ 号情况
如果新加的三条边 $E_{a_i},E_{b_i},E_{c_i}$ 去掉 $E_{b_i}$，那么这个图仍然为状态 $0$，如下图 $4$ 号情况
- 递推式均为：$dp[i][j+1][0]$ += $dp[i-1][j][0]$
如果新加的三条边 $E_{a_i},E_{b_i},E_{c_i}$ 去掉 $E_{a_i},E_{c_i}$，那么这个图会变成状态 $1$，如下图 $5$ 号情况
如果新加的三条边 $E_{a_i},E_{b_i},E_{c_i}$ 去掉 $E_{b_i},E_{c_i}$，那么这个图会变成状态 $1$，如下图 $6$ 号情况
- 递推式均为：$dp[i][j+2][1]$ += $dp[i-1][j][0]$

时间复杂度：$O(N^2)$

代码

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 3100;
long long dp[MAXN][MAXN][2];
int N, P;

int main()
{
    dp[0][0][0] = 1;
    dp[0][1][1] = 1;
    cin >> N >> P;
    for (int i = 1; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            dp[i][j][0] += dp[i - 1][j][1];
            dp[i][j][0] %= P;
            dp[i][j + 1][1] += dp[i - 1][j][1];
            dp[i][j + 1][1] %= P;
            dp[i][j][0] += dp[i - 1][j][0];
            dp[i][j][0] %= P;
            dp[i][j + 1][0] += 3 * dp[i - 1][j][0];
            dp[i][j + 1][0] %= P;
            dp[i][j + 2][1] += 2 * dp[i - 1][j][0];
            dp[i][j + 2][1] %= P;
        }
    }
    for (int i = 1; i < N; i++)
        cout << dp[N - 1][i][0] << ' ';
    return 0;
}

题目 | Keep Connect