题目 | One Fourth
AtCoder Beginner Contest 250
F - One Fourth
https://atcoder.jp/contests/abc250/tasks/abc250_f
Time Limit: 2 sec / Memory Limit: 1024 MB
Score : $500$ points
Problem Statement
ABC 250 is a commemorable quarter milestone for Takahashi, who aims to hold ABC 1000, so he is going to celebrate this contest by eating as close to $1/4$ of a pizza he bought as possible.
The pizza that Takahashi bought has a planar shape of convex $N$-gon. When the pizza is placed on an $xy$-plane, the $i$-th vertex has coordinates $(X_i, Y_i)$.
Takahashi has decided to cut and eat the pizza as follows.
- First, Takahashi chooses two non-adjacent vertices from the vertices of the pizza and makes a cut with a knife along the line passing through those two points, dividing the pizza into two pieces.
- Then, he chooses one of the pieces at his choice and eats it.
Let aa be the quarter ($=1/4$) of the area of the pizza that Takahashi bought, and bb be the area of the piece of pizza that Takahashi eats. Find the minimum possible value of $8 \times |a-b|$. We can prove that this value is always an integer.
Constraints
- All values in input are integers.
- $4 \le N \le 10^5$
- $|X_i|, |Y_i| \le 4 \times 10^8$
- The given points are the vertices of a convex $N$-gon in the counterclockwise order.
Input
Input is given from Standard Input in the following format:
$N$
$X_1$ $Y_1$
$X_2$ $Y_2$
$\dots$
$X_N$ $Y_N$
Output
Print the answer as an integer.
Sample Input 1
5
3 0
2 3
-1 3
-3 1
-1 -1
Sample Output 1
1
Suppose that he makes a cut along the line passing through the $3$-rd and the $5$-th vertex and eats the piece containing the $4$-th vertex.
Then, $a=\frac{33}{2} \times \frac{1}{4} = \frac{33}{8}$, $b=4$, and $8 \times |a-b|=1$, which is minimum possible.
Sample Input 2
4
400000000 400000000
-400000000 400000000
-400000000 -400000000
400000000 -400000000
Sample Output 2
1280000000000000000
Sample Input 3
6
-816 222
-801 -757
-165 -411
733 131
835 711
-374 979
Sample Output 3
157889
我的笔记
$O(N^3)$ 法:TLE x20
思路:
在 $P_0,P_1,\cdots,P_N$ (P代表点) 中任取 $P_i,P_j$,且 $P_i,P_j$ 不可相邻,规定吃掉包含 $P_{i+1}$ 的部分。所有情况 $8 \times |a-b|$ 的最小值即为所求。
求法:
$P_i,P_j$ 不相邻判断:$i,j$ 相差的绝对值不可 $\leq1$。并且也不能等于 $N-1$, 即 $i=0,j=N-1$ 或 $j=0,i=N-1$ 的情况。
包含 $P_{i+1}$ 的部分的面积求法:如图,$S_{BCDE}=S_{\triangle BCD}+S_{\triangle BDE}$,即将多边形以 $P_i$ 为顶点划分为三角形。
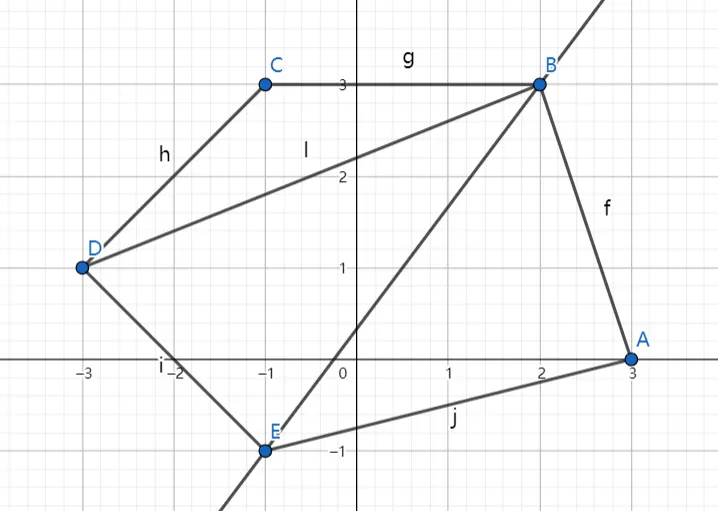
三角形面积:已知 $\triangle ABC$ 的三个顶点 $A(x_1,y_1),B(x_2,y_2),C(x_3,y_3)$,可以用向量叉乘表示面积: $2S_{\triangle ABC}=\overrightarrow{AB}\times\overrightarrow{AC}$,即:
$$ S_{\triangle ABC}=\frac{1}{2} \left|\begin{matrix} \vec{i} &\vec{j} &\vec{k} \\ x_2-x_1 &y_2-y_1 &0 \\ x_3-x_1 &y_3-y_1 &0 \\ \end{matrix}\right| =\frac{1}{2}\left|(x_3-x_1)(y_2-y_1)-(x_2-x_1)(y_3-y_1)\right| $$
代码:
#include <bits/stdc++.h>
using namespace std;
const int SIZE = 1e5 + 10;
int N;
pair<int, int> points[SIZE];
inline long long areax2(pair<int, int> a, pair<int, int> b, pair<int, int> c)
{
return abs(1ll * (c.first - a.first) * (b.second - a.second) - 1ll * (b.first - a.first) * (c.second - a.second));
}
int main()
{
cin >> N;
for (int i = 0; i < N; i++)
cin >> points[i].first >> points[i].second;
long long ax8 = 0;
for (int i = 1; i < N - 1; i++)
{
ax8 += areax2(points[0], points[i], points[i + 1]);
}
long long ans = INT64_MAX;
// START
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
if (abs(i - j) <= 1 || abs(i - j) == N - 1)
continue;
long long bx2 = 0;
for (int k = (i + 1) % N; k != j; k = (k + 1) % N)
{
bx2 += areax2(points[i], points[k], points[(k + 1) % N]);
}
ans = min(ans, abs(ax8 - 4 * bx2));
}
}
// END
cout << ans << endl;
return 0;
}$O(N^2)$ 法:TLE x11
上面的方法是从多边形分割为小三角形计算,同一个小三角形的面积重复计算了很多次。我们可以用小三角形的面积来组成多边形,可以减少很多次计算。
思路:
在 $P_0,P_1,\cdots,P_N$ 任取 $P_i$,逆时针方向依次加上以 $P_i$ 为顶点的小三角形的面积,每次加上后计算一次结果的最小值。
如下图,若取 $B$ 为顶点,那么计算 $S_{\triangle BCD},S_{\triangle BCD}+S_{\triangle BDE}$,依此为吃掉的面积计算 $8 \times |a-b|$ 的结果。
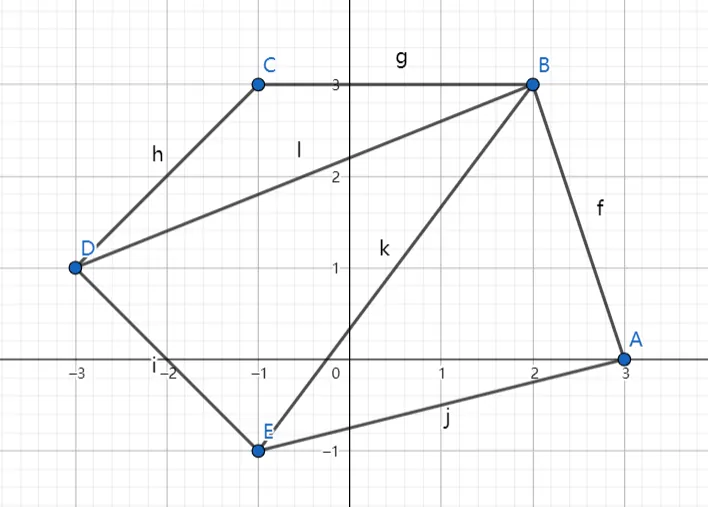
求法:
取 $j=(i+1)\bmod N$,将已有面积加上以 $P_i,P_j,P_{(j+1)\bmod N}$ 为顶点的三角形的面积,每次操作后将 $j$ 更新为 $(j+1)\bmod N$,一共进行 $N-2$ 次操作(因为不能沿着边切割)
取模很重要!只要是 $+1$ ,序号都有可能超过 $N$ 而重新从 $0$ 开始。
代码:
// 将此代码替换到方法一代码的START注释与END注释之间
for (int i = 0; i < N; i++)
{
long long bx2 = 0;
for (int j = (i + 1) % N, t = 0; t < N - 2; j = (j + 1) % N, t++)
{
bx2 += areax2(points[i], points[j], points[(j + 1) % N]);
ans = min(ans, abs(ax8 - 4 * bx2));
}
}$O(N)$ 法:AC
思路:
既然题目要求 $8 \times |a-b|$ 最小,那么可以用滑动窗口:若 $b<a$,那就是切少了,得多切点;若 $b>a$,那就是切多了,得少切点。
求法:
$i$ 初始为 $0$,$j$ 初始为 $1$,如果 $b<a$,那么加上以 $P_i,P_j,P_{(j+1)\bmod N}$ 为顶点的三角形面积,$j$ 更新为 $(j+1)\bmod N$ 然后再继续加三角形,直到 $b\geq a$。然后再去掉以 $P_i,P_{(i+1)\bmod N},P_j$ 为顶点的三角形面积,$i$ 加一,直到 $b<a$.
代码:
// 将此代码替换到方法一代码的START注释与END注释之间
long long bx2 = 0;
int j = 1;
for (int i = 0; i < N; i++)
{
while (bx2 * 4 < ax8)
{
bx2 += areax2(points[i], points[j], points[(j + 1) % N]);
j = (j + 1) % N;
ans = min(ans, abs(ax8 - 4 * bx2));
}
bx2 -= areax2(points[i], points[(i + 1) % N], points[j]);
ans = min(ans, abs(ax8 - 4 * bx2));
}本文采用 CC BY-SA 4.0 许可,本文 Markdown 源码:Haotian-BiJi