树状数组 (Binary Index Tree, BIT / Fenwick Tree): 对于满足结合律且可差分的问题，可在 $O(\log n)$ 进行单点修改和区间查询的数据结构。

满足结合律且可差分的问题：对于运算 $\circ$，如果其存在逆运算 $\bullet$，即 $x\circ y\bullet y=x$，则该运算是可差分的。若该运算同时满足结合律，则是满足结合律且可差分的问题。符合这个性质的常见运算有 $+,\times,\oplus$.

树状数组

时间复杂度：$O(\log n)$

单点修改和区间查询均为该复杂度。

分析

意义

首先我们来看两种数组，一种是普通数组，长度为 $n$：

$$ 1,2,3,4,5,6,7,8,\cdots $$

对于上面这个普通数组，单点修改时间复杂度 $O(1)$，但区间求和的复杂度为 $O(n)$。

我们可以用前缀和优化，变成长度为 $n$ 的前缀和数组：

$$ 1,3,6,10,15,21,28,36,\cdots $$

对于上面这个前缀和数组，区间求和的时间复杂度为 $O(1)$，但单点修改的复杂度为 $O(n)$。

可以发现以上两种数组都有长处和短处，但根据木桶效应，要想整体优秀，最好还是各方面平衡。树状数组便是平衡了这两种操作的时间复杂度的数据结构，它将其平均为了 $O(\log n)$。

原理及代码

普通数组单点修改快，是因为每一个元素都是独立的。前缀和数组区间求和快，是因为它的元素就是区间的和。为了平衡，我们可以将其变为一个个独立小区间，这样单点修改时只需要修改小区间，无需整个修改。区间求和时可以直接用小区间求和，也可以少算很多步。这时小区间的排布非常重要，如何才能达到最好的效果。

区间排布

树状数组的区间排布用的是二进制思想，就其英文名“二进制下标树”也可以知道这点。其排布如下图所示：

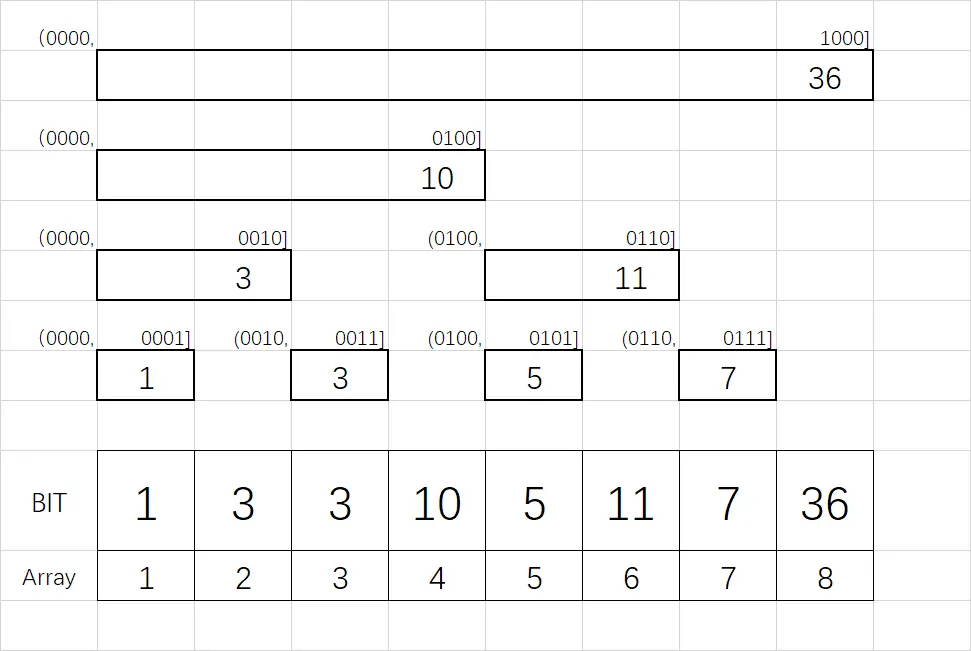
Array 为原数组，BIT 为转化为的树状数组，数组下标均从 $1$ 开始。用二进制来表示树状数组的下标，其第 $i$ 位储存区间 $(i-\mathrm{lowbit}(i),i]$ 的和。其中 $\mathrm{lowbit}(i):=$ 二进制数 $i$ 的最右边的一个 $1$ 连带后面的 $0$.

这么说还是不够形象，举几个例子：

$\mathrm{lowbit}(0111)=1$，$0111-\mathrm{lowbit}(0111)=0110$，那么树状数组第 $0111$ 位储存 $(0110,0111]$ 的和；

$\mathrm{lowbit}(0100)=100$，$0100-\mathrm{lowbit}(0100)=0000$，那么树状数组第 $0100$ 位储存 $(0000,0100]$ 的和。

用通俗易懂的话来说：

第 $i$ 位储存的区间，右端点就是 $i$（闭），左端点就是把 $i$ 二进制表示中最靠右的 $1$ 变成 $0$（开）

const int MAXN = 1e6;
int Fenwick_Tree[MAXN];
// 如果不是全局变量记得初始化为0

区间求和

例如我们要求区间 $(0000,0111]$ 的和，我们需要将区间 $(0000,0100],(0100,0110],(0110,0111]$ 相加。通过观察可以发现，这就是不断减去 $\mathrm{lowbit}(i)$，到 $0$ 为止。

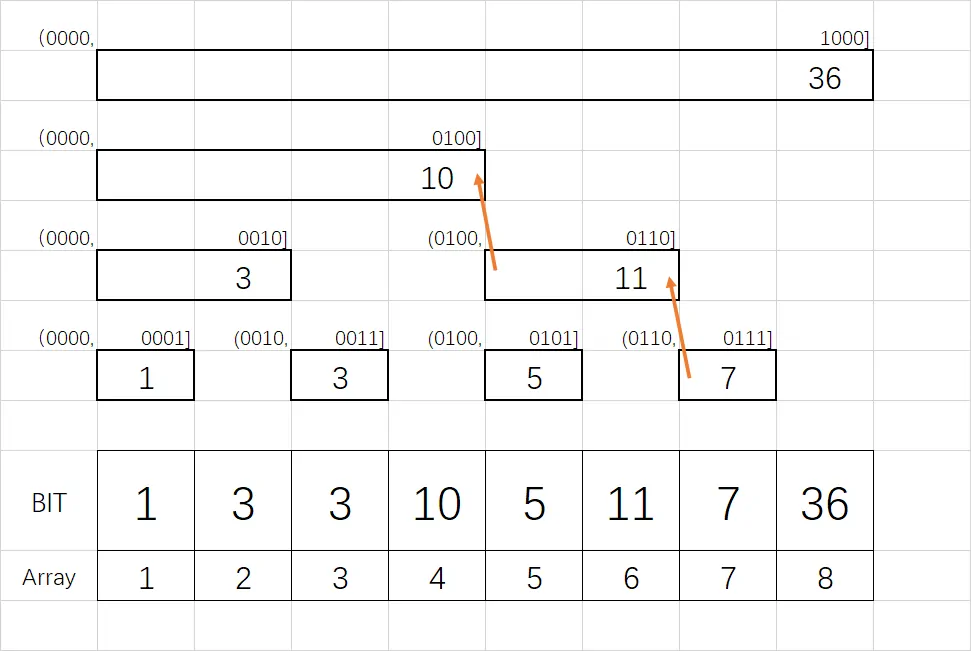
此时我们需要用到 $\mathrm{lowbit}(x)$ 这个函数的求法，其实很简单 $\mathrm{lowbit}(x)=(x)\&(-x)$，能这么用主要是因为计算机中有符号整型的储存方式，即用补码来储存，如下面例子：

$$ \begin{align} 原码:&010111100\\ 反码:&101000011\\ 补码: &101000100\\ 原码\&补码:&000000100 \end{align} $$

我们知道正数的原码等于补码，那么一个数和自己的相反数做按位与，便是原码和补码做按位与，即可计算出 $\mathrm{lowbit}(x)$.

// 查询(0,pos]的区间和
int query(int pos)
{
    int ans = 0;
    for (int i = pos; i; i -= i & -i)
        ans += Fenwick_Tree[i];
    return ans;
}

以上计算的是从 $0$ 开始的区间和，如果区间左端不是 $0$，那么可以进行转化，即转化为两个从 $0$ 开始的区间和之差。

// 查询[l,r]的区间和
inline int query(int l, int r)
{
    return query(r) - query(l - 1);
}

单点修改

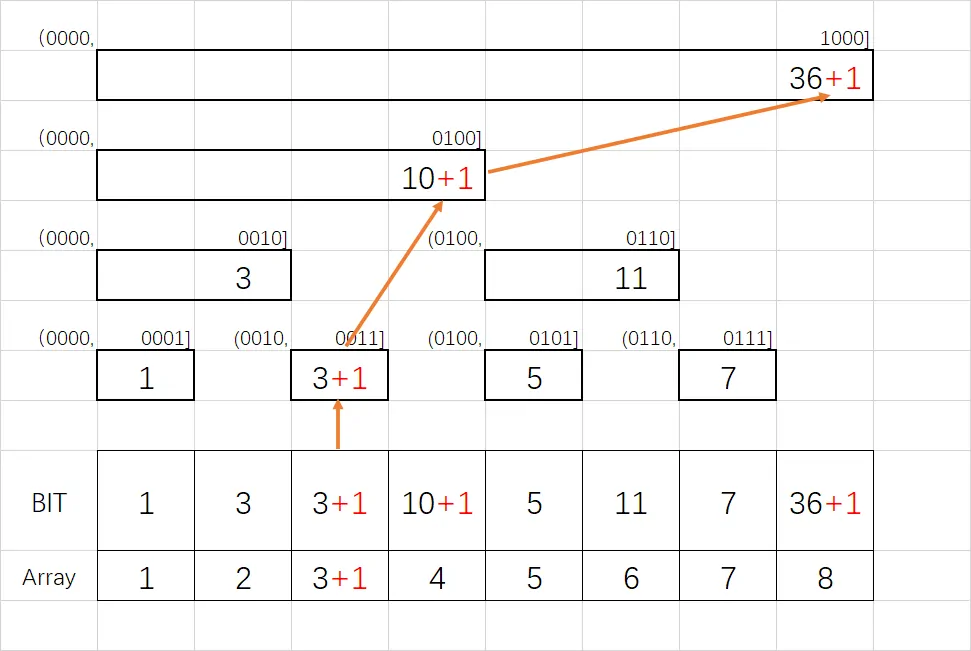
例如我们要将第 $0011$ 位的值 $+1$，我们需要找到包含该位数据的所有区间，即 $(0010,0011],(0000,0100],(0000,1000]$，然后将这三个区间的值均 $+1$。通过观察可发现，这就是不断加上 $\mathrm{lowbit}(i)$，到最大下标为止。

// 第pos位加上val
void update(int pos, int val)
{
    for (int i = pos; i < MAXN; i += i & -i)
        Fenwick_Tree[i] += val;
}