原数组：$[3,1,4,1,5,9]$
前缀和：$[3,4,8,9,14,23]$
差分：$[3,-2,3,-3,4,4]$

前缀和

通过前缀和数组，可以以 $O(1)$ 的复杂度查询到一个连续区间内元素的和。

一维

构造方式

$$ ps[i]=ori[1]+ori[2]+\cdots+ori[i] $$

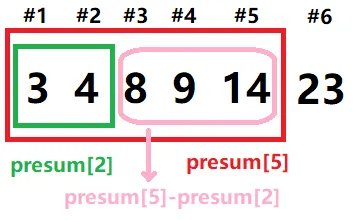
查询方式

$$ ori[l]+\cdots+ori[r]=ps[r]-ps[l-1] $$

二维

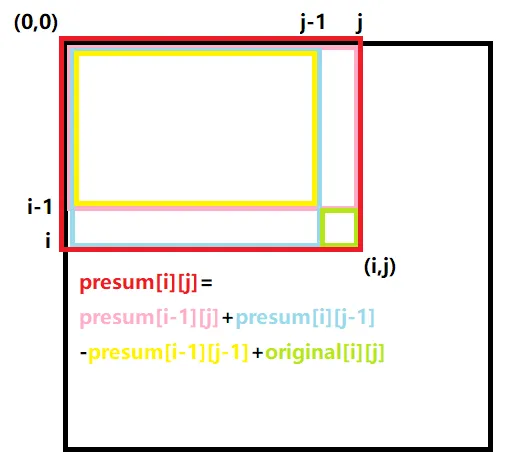
构造方式

$$ ps[i][j]=ps[i-1][j]+ps[i][j-1]-ps[i-1][j-1]+ori[i][j] $$

查询方式

$$ \begin{align} &(x_1,y_1)为左上顶点(x_2,y_2)为右下顶点的矩阵的总和\\ =\ &ps[x_2][y_2]-ps[x_1-1][y_2]-ps[x_2][y_1-1]+ps[x_1-1][y_1-1] \end{align} $$

原理与上图类似，因此不画图了。

差分

通过差分数组，可以以 $O(1)$ 的复杂度向一个连续区间内元素加上一个数。

一维

构造方式

$$ df[i]=ori[i]-ori[i-1] $$

或者写成与下面统一的形式：

$$ \begin{align} df[i]\ &+\!=ori[i]\\ df[i+1]\ &-\!=ori[i] \end{align} $$

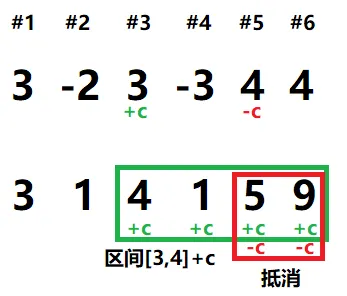
修改方式

给区间 $[l,r]$ 中每个数 $+c$：

$$ \begin{align} df[l]\ &+\!=c\\ df[r+1]\ &-\!=c \end{align} $$

二维

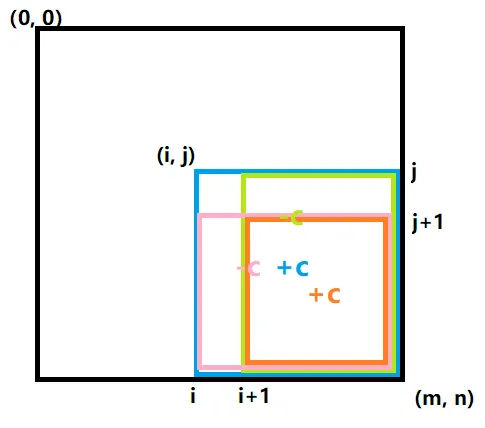
构造方式

$$ \begin{align} df[i][j]\ &+\!=ori[i][j]\\ df[i+1][j]\ &-\!=ori[i][j]\\ df[i][j+1]\ &-\!=ori[i][j]\\ df[i+1][j+1]\ &+\!=ori[i][j] \end{align} $$

修改方式

给区间 $(x_1,y_1)为左上顶点(x_2,y_2)为右下顶点的矩阵$ 中每个数 $+c$：

$$ \begin{align} df[x_1][y_1]\ &+\!=c\\ df[x_2+1][y_1]\ &-\!=c\\ df[x_1][y_2+1]\ &-\!=c\\ df[x_2+1][y_2+1]\ &+\!=c \end{align} $$

原理与上图类似，因此不画图了。