堆 (Heap)：是计算机科学中的一种特别的完全二叉树，最高效的优先级队列。

堆

性质

• 堆是一个完全二叉树。

完全二叉树：一棵深度为 $k$ 的有 $n$ 个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为 $i\ (1\leq i\leq n)$ 的结点与满二叉树中编号为 $i$ 的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

• 给定堆中任意节点 $P$ 和 $C$，若 $P$ 是 $C$ 的父节点，那么 $\text{P的值}\leq\text{C的值}$（此即为小根堆，若 $\geq$ 则为大根堆）。
• 在堆中最顶端的那一个节点，称作根节点，根节点没有父节点。

下图可以形象地反映上述三条性质。另外下文均以小根堆举例。

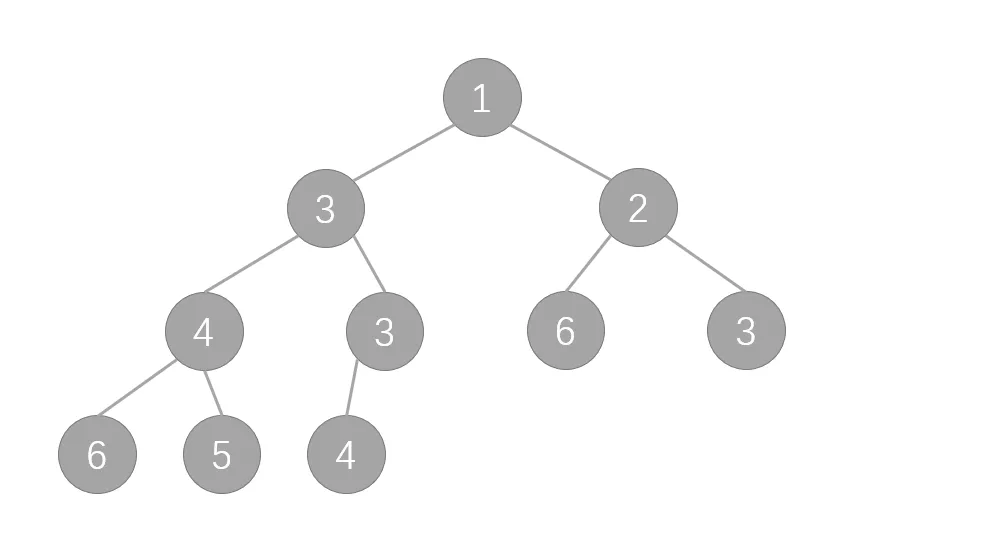
堆的储存

代码实现上，通常将堆储存在一维数组内。以下标 $1$ 为根节点，下标 $x$ 的左儿子下标为 $2x$，右儿子下标为 $2x+1$，如下图所示。

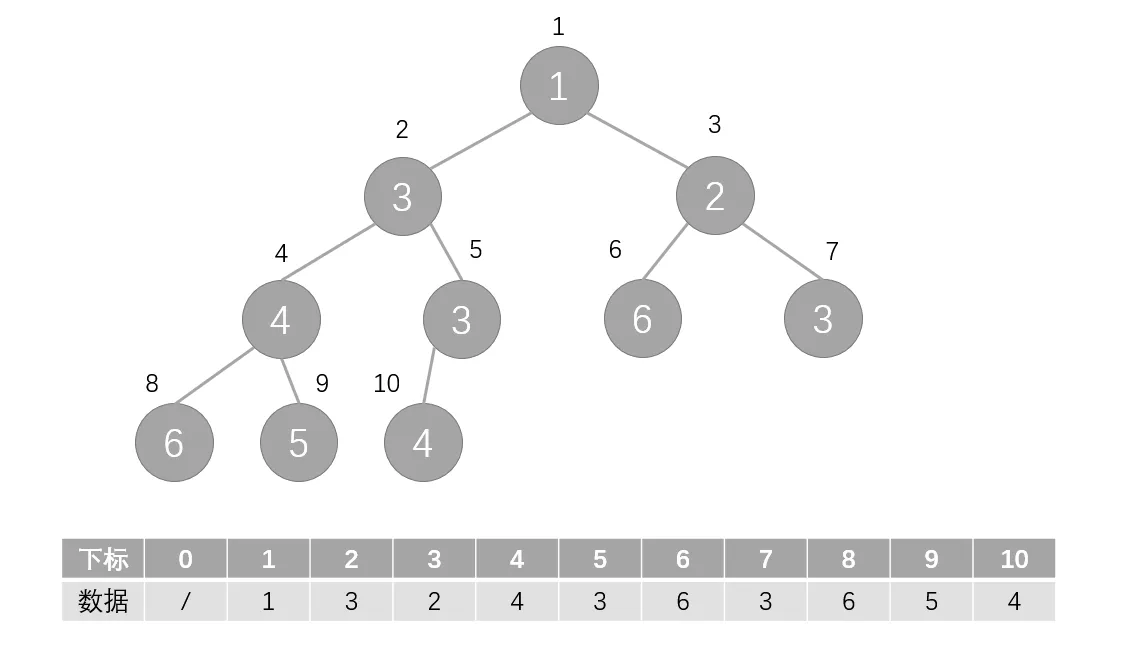
代码：

const int MAXN = 1e6 + 10; // 堆的最大大小
int heap[MAXN];            // 储存堆的数组
int idx;                   // 堆的当前大小

堆的基本操作

1. 上滤 (Percolate Up)

若我们修改堆中一个节点使其变小，且小于父节点，那么此时它的位置不符合堆的性质，我们要通过上滤操作将其移动到正确的位置。

若对节点 $x$ 做上滤操作，首先判断父节点（即节点 $x/2$）是否大于节点 $x$，若大于，则交换这两个节点。再重复前面的操作，直到根节点为止。

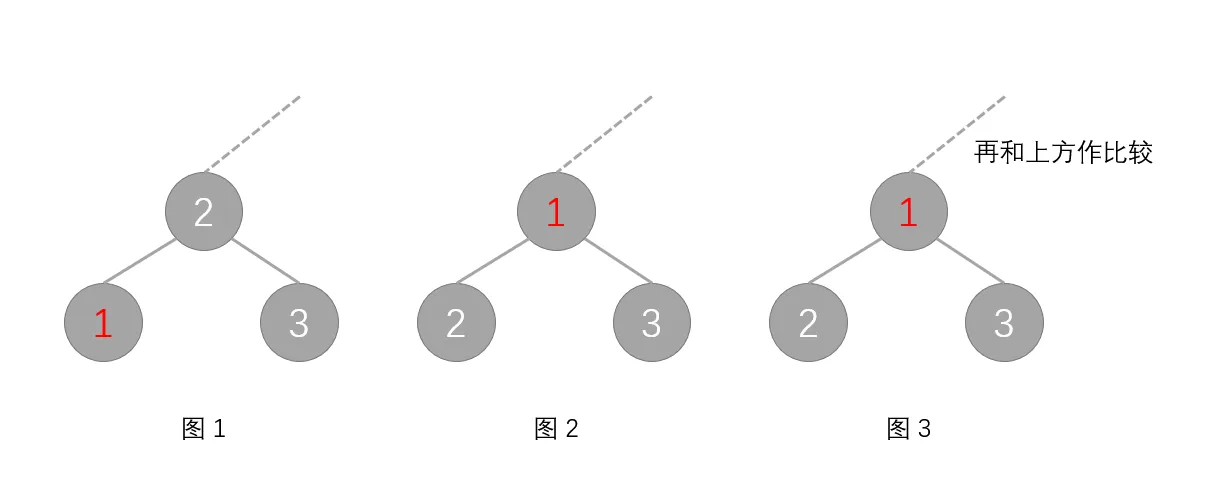
时间复杂度：$O(\log n)$

代码：

void up(int u)
{
    while (u / 2 && heap[u] < heap[u / 2])
    {
        swap(heap[u], heap[u / 2]);
        u /= 2;
    }
}

2. 下滤 (Percolate Down)

若我们修改堆中一个节点使其变大，且大于子节点，那么此时它的位置不符合堆的性质，我们要通过下滤操作将其移动到正确的位置。

若对节点 $x$ 做下滤操作，首先要找到该节点和它的两个子节点（即节点 $2x$、节点 $2x+1$）中最小的节点，若最小的节点不是自己，则交换这两个节点。再重复前面的操作，直到没有子节点为止。

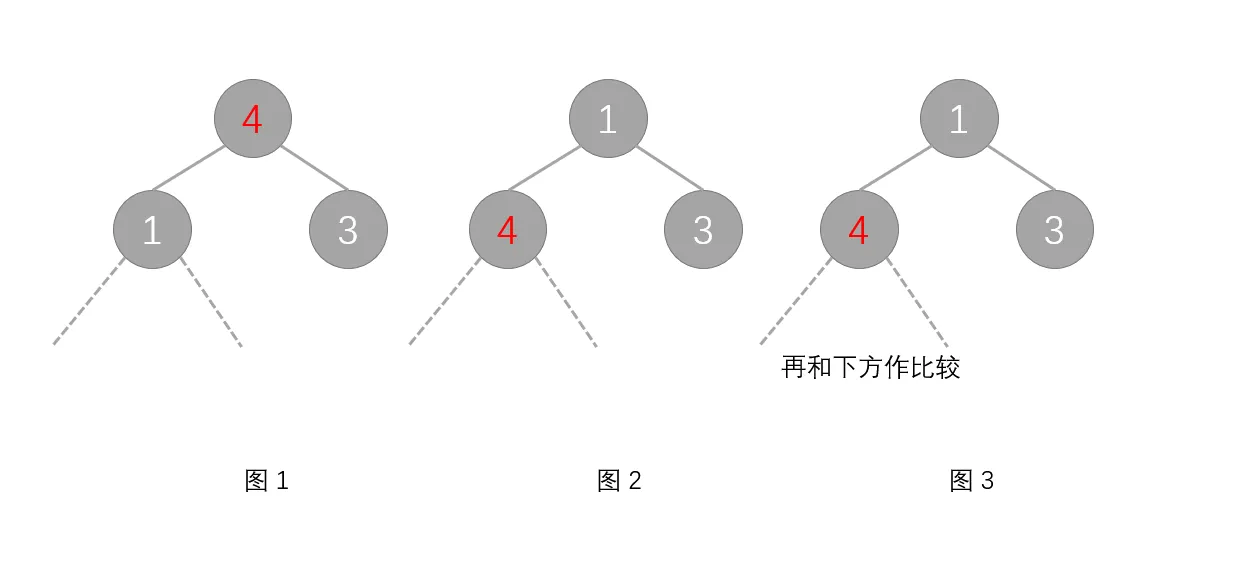
为什么要找最小的节点？可以假设不这么做，将 $4$ 与 $3$ 交换，然后发现 $3>1$ 仍然不满足堆的条件。若与最小的节点交换则可以保证满足堆的条件。

时间复杂度：$O(\log n)$

代码：

void down(int u)
{
    int t = u;
    if (u * 2 <= idx && heap[u * 2] < heap[t])
        t = u * 2;
    if (u * 2 + 1 <= idx && heap[u * 2 + 1] < heap[t])
        t = u * 2 + 1;
    if (t != u)
    {
        swap(heap[t], heap[u]);
        down(t);
    }
}

堆的扩展操作

通过上述两种基本操作，我们可以组合出许多扩展操作。

1. 无序数列建堆

直接从 $size/2$ 处反向 down 到 $1$，即可保证数列是一个堆。

时间复杂度：$O(n)$

代码：

for (int i = n / 2; i > 0; i--)
    down(i);

2. 取得堆中最小值

堆顶即为最小值。

时间复杂度：$O(1)$

代码：略

3. 向堆中插入一个数

将该数插入数列尾部，再做上滤即可。

时间复杂度：$O(\log n)$

代码：

// num 为待插入的数
heap[++idx] = num;
up(idx);

4. 删除任意一个元素

用数列尾部的数覆盖掉待删除的数，删除数列尾部，再对该元素做一遍上滤，再做一遍下滤。

之所以既做上滤又做下滤，是为了免去判断、简化代码。运行时实际上只进行了一个操作，不符合条件的操作在运行时会立即退出。

时间复杂度：$O(\log n)$

代码：

// id 为待删除节点的编号
heap[id] = heap[idx--];
up(id);
down(id);

5. 修改任意一个元素

修改对应元素，然后对该元素做一遍上滤，再做一遍下滤。

时间复杂度：$O(\log n)$

代码：

// id 为待修改节点的编号，num 为新数值
heap[id] = num;
up(id);
down(id);

带映射的堆

上面的堆可以对编号为 $n$ 的节点进行操作，但如果我们要对第 $n$ 个插入的节点做操作，那就没有办法了。因为上面实现的堆没有记录第 $n$ 个插入的节点对应堆中的编号，因此找不到待操作的节点。

储存映射关系

为了实现这个功能，我们需要额外引入两个数组：

$$ \begin{align} ph(x)&=第x个插入的节点在堆中的编号\\ hp(x)&=在堆中编号为x的节点插入的序号 \end{align} $$

这两个数组实际上互为反函数，即 $hp=ph^{-1}$.

我们可能会想，我们似乎只需要 ph 数组即可，为什么还需要 hp 呢？原因是为了维护它们。如果我们要交换节点 $i$ 和节点 $j$，我们需要将指向它们的 ph 数组也进行交换，我们需要依靠 hp 数组才能找到他们，即 ph[hp[i]] 和 ph[hp[j]]。

维护方式

修改节点交换的代码

首先节点的交换方式需要变化，我们交换节点 $i$ 和节点 $j$ 时，也得将对应指针也交换。

// 注意该函数的形参 a, b 是下标，和内置的 swap 函数不同。
inline void heap_swap(int a, int b)
{
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(heap[a], heap[b]);
}

我们需要将之前 up 和 down 函数使用的 swap 函数全部替换为上面的 heap_swap 函数。

修改扩展操作的代码

inline void insert(int num)
{
    idx++; 
    id++;
    heap[idx] = num;
    ph[id] = idx;    // 建立插入序号->节点编号的映射
    hp[idx] = id;    // 建立节点编号->插入序号的映射
    up(idx);
}

inline int getmin()
{
    return heap[1];
}

inline void erase()
{
    heap_swap(1, idx); // 用heap_swap而不是直接赋值，才能维护映射关系
    idx--;
    down(1);
}

inline void erase(int id)
{
    int k = ph[id];    // 需要先储存k，防止操作过程中变化
    heap_swap(k, idx); // 用heap_swap而不是直接赋值，才能维护映射关系
    idx--;
    up(k);
    down(k);
}

inline void modify(int id, int num)
{
    int k = ph[id]; // 需要先储存k，防止操作过程中变化
    heap[k] = num;
    up(k);
    down(k);
}