Bellman-Ford 算法

复杂度

时间复杂度：$O(\left|V\right|\cdot\left|E\right|)$

（$\left|V\right|$ 为顶点数，$\left|E\right|$ 为边数）

分析

Dijkstra 算法仅对确定点的出边做松弛操作，Bellman-Ford 算法更为暴力，每次迭代对所有的边做松弛操作，共进行 $\left|V\right|-1$ 次迭代。在重复的计算中，最短路径可以被多次更新，正确最短距离的边随着计算不断增加，直到最后一次迭代，所有的边都计算正确。这也是为什么该算法能够处理赋权边。

伪代码如下：

bellman_ford(G, dist[])
    初始化: dist[1~V]=+INF, dist[1]=0
    for (循环V-1次)
        for (t : 所有边的集合)
            if (以t为中介点到s的距离更短)
                更新dist[s];

迭代次数

上述进行 $\left|V\right|-1$ 次迭代实际上是最大迭代次数，实际有可能在 $\left|V\right|-1$ 次前就已经计算出了所有最短路径。因此可以增加判断，若一次迭代中没有发生松弛操作，即可跳出循环结束算法。

迭代次数实际上也有意义，若进行 $k$ 次迭代，产生的结果便是经过 $\leq k$ 个边的最短路径。因此该算法可以很好地解决“有边数限制的最短路问题”。

负权回路

当图中出现负权回路时，有可能不存在最短路，示例如下：

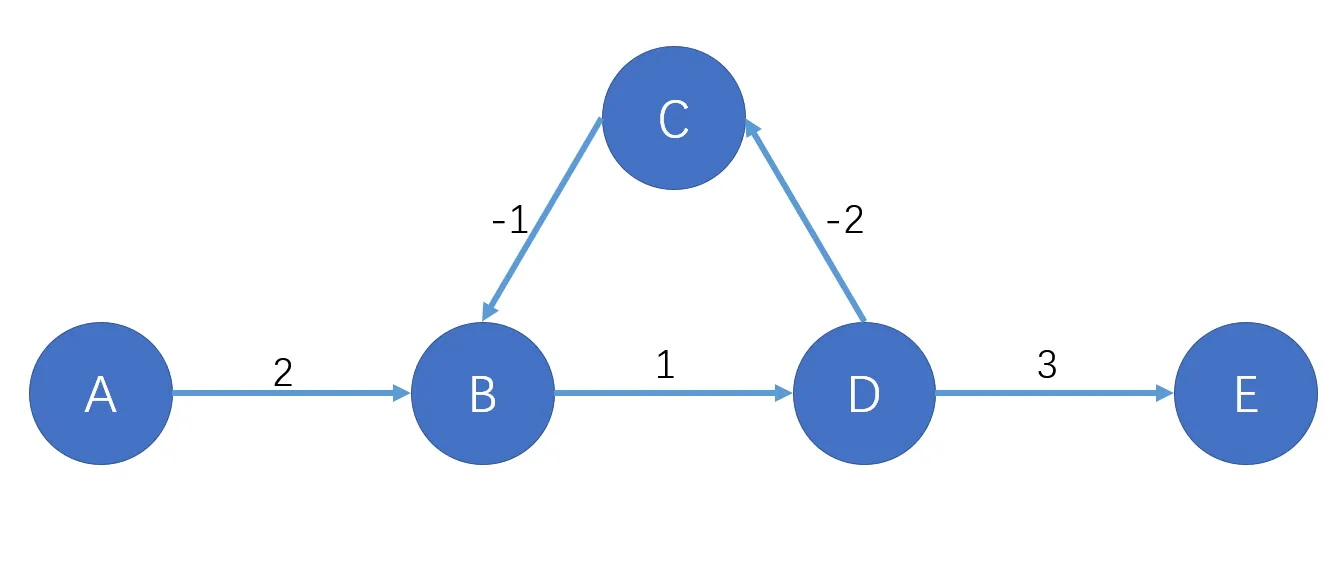
$B\rightarrow D\rightarrow C\rightarrow\cdots$ 为一个回路，该回路的权值为 $1+(-2)+(-1)=-2$，即负权回路。若要求 $A\rightarrow E$ 的最短路，我们可以在负权回路中绕任意次，每绕一次路径长度 $-2$。因此 $A\rightarrow E$ 的距离可以为 $-\infty$，因此不存在最短路径。

若要判断是否有负权回路，可以在 $\left|V\right|-1$ 次后额外进行一次迭代，若第 $\left|V\right|$ 次迭代又发生了松弛操作，则可以确定图中存在负权回路。

无穷大判断

由于在代码实现中我们往往使用一个较大的数作为 $\infty$，例如 0x3f3f3f3f. 而在该算法中，有可能出现以下松弛操作：

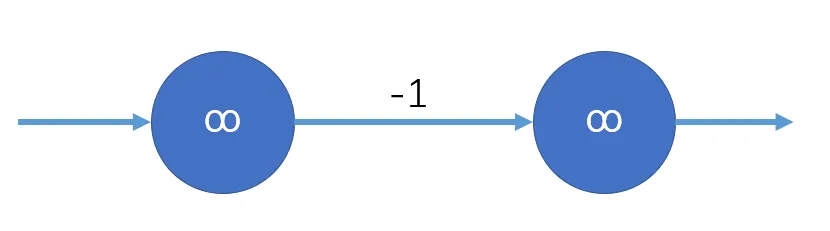
松弛后，后者的值变成了 $\infty-1$。虽然在数学中 $\infty-1=\infty$，但在程序中 $\text{0x3f3f3f3f}$ 不等于 $\text{0x3f3f3f3f}-1$，此时对于无穷大的判断就会产生问题。为了规避这个问题，我们可以判断一个数若 $\geq \text{0x3f3f3f3f}/2$ 就为 $\infty$，在一般情况下，是不会出现错误的。

串联问题

在代码实现中，若每次迭代使用的就是本次迭代的值，很有可能产生串联问题，即本次迭代中前面计算出的值被后面的计算使用，这样会产生错误。为了限制本次迭代使用的值一定为上次迭代的值，我们需要备份保存一遍上次的值，对应下面代码中 memcpy 语句。

代码实现

由于该算法只需遍历所有的边即可，所以存图方法比较简单粗暴，直接用一个结构体数组存下来所有边即可。

const int MAXN = 510, MAXM = 1e4 + 10, INF = 0x3f3f3f3f;
int v, e, k;                  // v顶点数 e边数 k经过边数限制
int dist[MAXN], backup[MAXN]; // dist最短距离 backup备份上一次迭代
struct Edge
{
    int a, b, w;              // a起点 b终点 w权值  
} edges[MAXM];                // 结构图数组存边

int bellman_ford()
{
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    for (int i = 0; i < k; i++)
    {
        memcpy(backup, dist, sizeof(dist));
        for (int j = 0; j < e; j++)
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            dist[b] = min(dist[b], backup[a] + w);
        }
    }
    return dist[v] > INF / 2 ? INF : dist[v];
}

算法 | Bellman-Ford 算法