容斥原理：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

容斥原理

描述

若 $A_1,\dots,A_n$ 为有限集，则

$$ {\displaystyle {\begin{aligned}\left|\bigcup _{i=1}^{n}A_{i}\right|={}&\sum _{i=1}^{n}|A_{i}|-\sum _{1\leq i<j\leq n}|A_{i}\cap A_{j}|+\sum _{1\leq i<j<k\leq n}|A_{i}\cap A_{j}\cap A_{k}|-\cdots +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|.\end{aligned}}} $$

其中 $\left|A\right|$ 表示 $A$ 的基数。

举例

我们用图片举例分析，我们要求 $|A\cup B\cup C|$，可以先求 $|A|+|B|+|C|$，发现有三个重复部分，那就再减去 $|A\cap B|,|B\cap C|,|A\cap C|$，发现减多了一个部分，那就再补回去一个 $|A\cap B\cap C|$

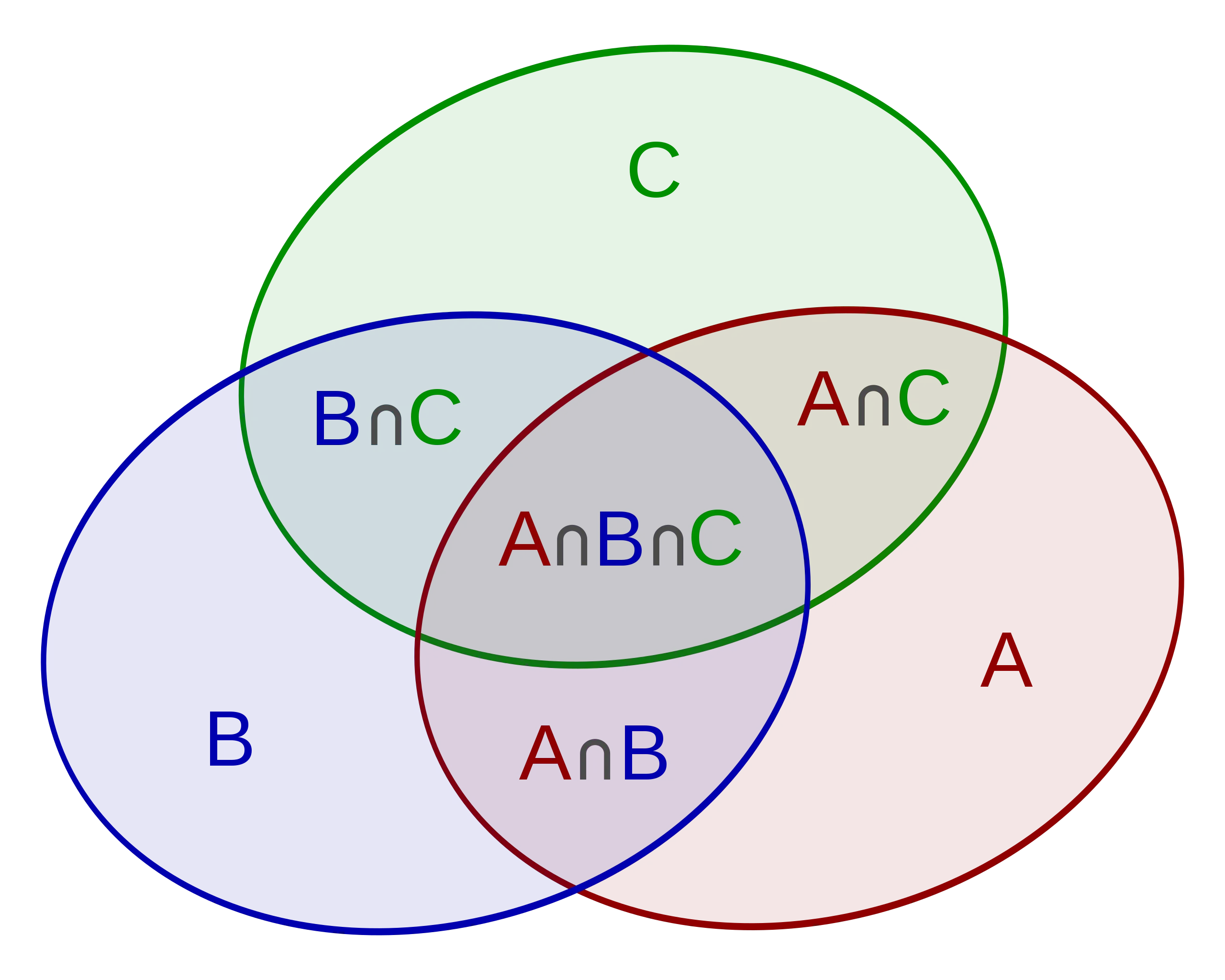
（图片和公式来源：维基百科，使用 CC BY-SA 3.0 协议）

代码实现

在容斥原理中，我们枚举了 $A_1,\dots,A_n$ 的所有选择情况，一共 $2^n$ 种情况。我们可以使用 DFS 进行遍历，但通常我们使用二进制的方法进行遍历会更方便。

我们可以将每种选择情况对应到一个 $n$ 位的二进制数上，例如：选 $A_2$ 对应 $\overbrace{0\dots0010}^{n位}$，选 $A_1,A_3$ 对应 $\overbrace{0\dots0101}^{n位}$. 那么我们从 $1$ 遍历到 $2^n-1$ 即可将（除不选的）所有选择情况全部遍历到。如果可以全不选的话，从 $0$ 开始遍历。

那么我们怎么得知某一位是否为 $1$ 呢？使用位运算，i >> n & 1 如果为 $1$ 那么就说明 $i$ 的第 $n$ 位为 $1$. 例如：

$$ \begin{align} i &=0001\ 0010\ 0100\ 0011\\ i\gg6 &=0000\ 0000\ 0100\ 1001\\ 1 &=0000\ 0000\ 0000\ 0001\\ i\gg6\ \&\ 1&=0000\ 0000\ 0000\ 0001\\ \end{align} $$

for (int i = 1; i < (1 << n); i++)
    for (int j = 0; j < n; j++)
        if (i >> j & 1)
            ...

实际应用中，往往需要按题目调整位运算的方式，但总体思路仍然是使用二进制数来遍历。