题目 | Hossam and Friends

Codeforces Round #837 (Div. 2)

B. Hossam and Friends

https://codeforces.com/contest/1771/problem/B

2 seconds / 256 megabytes

standard input / standard output

Problem

Hossam makes a big party, and he will invite his friends to the party.

He has $n$ friends numbered from $1$ to $n$. They will be arranged in a queue as follows: $1,2,3,\dots ,n$.

Hossam has a list of $m$ pairs of his friends that don't know each other. Any pair not present in this list are friends.

A subsegment of the queue starting from the friend $a$ and ending at the friend $b$ is $[a,a+1,a+2,\dots ,b]$. A subsegment of the queue is called good when all pairs of that segment are friends.

Hossam wants to know how many pairs $(a,b)$ there are ($1\le a\le b\le n$), such that the subsegment starting from the friend $a$ and ending at the friend $b$ is good.

Input

The input consists of multiple test cases. The first line contains a single integer $t$ ($1\le t\le 2\cdot {10}^4$), the number of test cases. Description of the test cases follows.

The first line of each test case contains two integer numbers $n$ and $m$ ($2\le n\le {10}^5$, $0\le m\le {10}^5$) representing the number of friends and the number of pairs, respectively.

The $i$-th of the next $m$ lines contains two integers $x_i$ and $y_i$ ($1\le x_i,y_i\le n$, $x_i\ne y_i$) representing a pair of Hossam's friends that don't know each other.

Note that pairs can be repeated.

It is guaranteed that the sum of $n$ over all test cases does not exceed ${10}^5$, and the sum of $m$ over all test cases does not exceed ${10}^5$.

Output

For each test case print an integer — the number of good subsegments.

Example

Input

2
3 2
1 3
2 3
4 2
1 2
2 3

Output

4
5

Note

In the first example, the answer is $4$.

The good subsegments are:

[1]

[2]

[3]

[1, 2]

In the second example, the answer is $5$.

The good subsegments are:

[1]

[2]

[3]

[4]

[3, 4]

题解

记录方式

对于一对不认识的人 $(a,b)$，我们的子序列是不可以同时囊括他们两个的，最多能包含他们其中一个，因此我们可以记录每个人他不认识的人的位置。

我们记录的方式为每一对中编号大的指向编号小的，如下图蓝色箭头表示的为 $(3,6),(5,8)$。

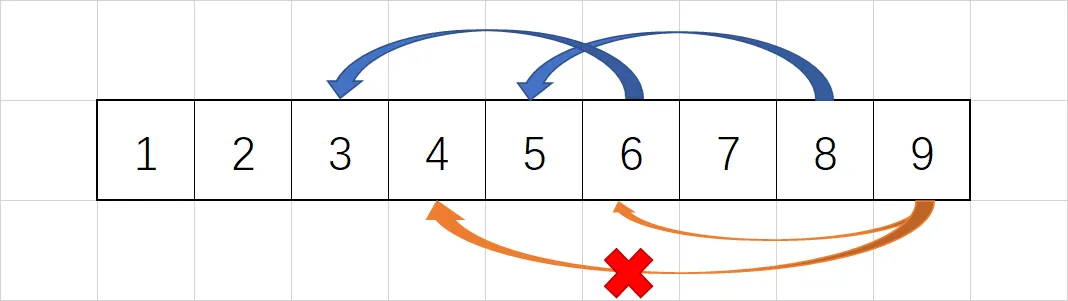
然后我们来考虑子序列是否合法，如上图橙色箭头。子序列 $[6,9]$ 是合法的，因为其只包含了每一对不认识的人中的一个人，但子序列 $[4,9]$ 是不合法的，因为其包含了 $(5,8)$ 这一对不认识的人。

计算方式

我们知道了记录方式，那么如何快速地进行计算呢？我们首先把上图的箭头改为数组的记录方式，如下面的第一行。然后再从左到右取最大值，如下面的第二行：

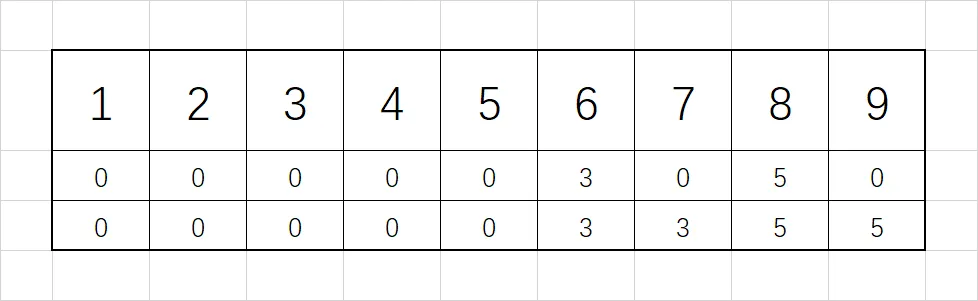
这样对于每一个元素，它的下标作为右端点，第二行的数据就是子序列的左端点不能越过的下标。如 $8$ 作为右端点，对应的数据为 $5$，就意味着左端点不可 $\le 5$，那么左端点能为 $6,7,8$ 共三种。

这样我们遍历一遍数组，就能得到答案为：

$$ans=\sum _{i=1}^{n}i-a_i$$

代码

#include <bits/stdc++.h>
#define int long long
#define endl '\n'

using namespace std;

const int MAXN = 1e5 + 10;
int n, m;
int a[MAXN];

void solve()
{
    memset(a, 0, sizeof(a));
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int x, y;
        cin >> x >> y;
        if (x < y)
            swap(x, y);
        a[x] = max(a[x], y);
    }
    for (int i = 2; i <= n; i++)
        a[i] = max(a[i], a[i - 1]);
    int ans = 0;
    for (int i = 1; i <= n; i++)
        ans += i - a[i];
    cout << ans << endl;
}

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}