大 O 符号：又称为渐进符号，是用于描述函数渐近行为的数学符号。在数学中，它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项；在计算机科学中，它在分析算法复杂性的方面非常有用。

紧确界记号 $\Theta$

  • 记法：$f(n)=\Theta(g(n))$
  • 解释：$f$ 的紧确界为 $g$
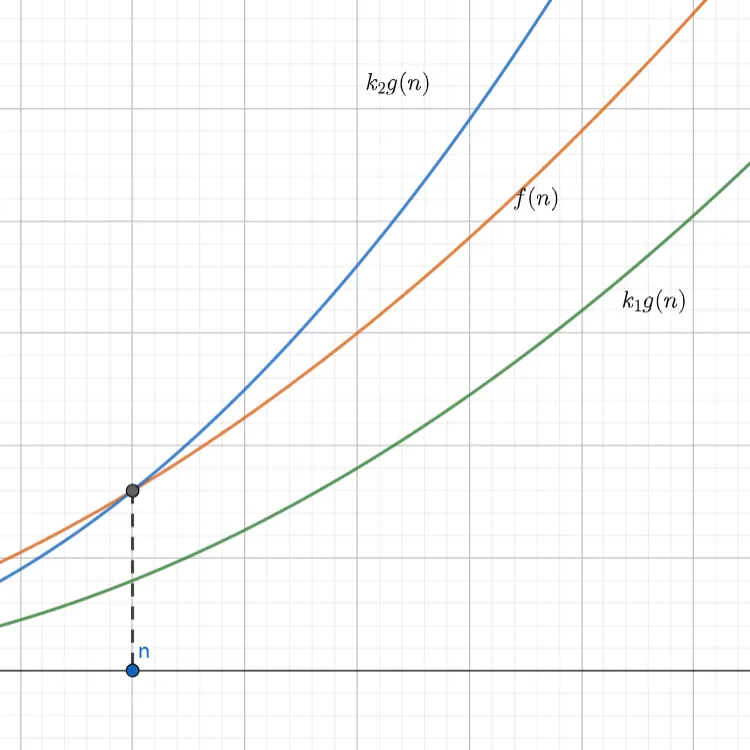
  • 形式化定义：$\exists k_1>0\,\exists k_2>0\,\exists n_0\,\forall n>n_0\colon\; k_1 g(n)\leq f(n)\leq k_2 g(n)$

在算法分析中，代表算法运行时间的确界。如 $\Theta(n^2)$ 代表算法运行时间的渐近增长速度和 $n^2$ 一样快。

渐进上界记号 $O$

  • 记法：$f(n)=O(g(n))$
  • 解释：$f$ 的渐近上界为 $g$
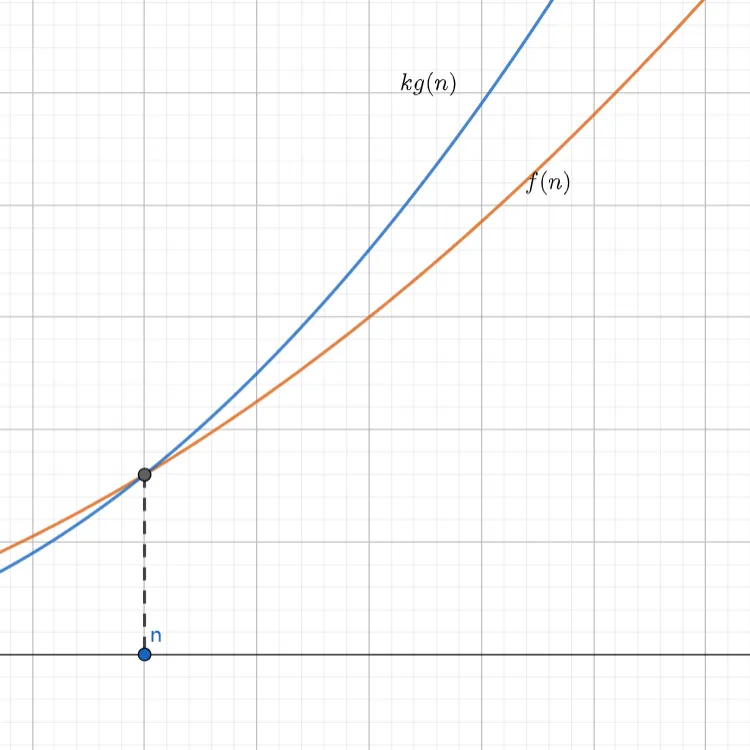
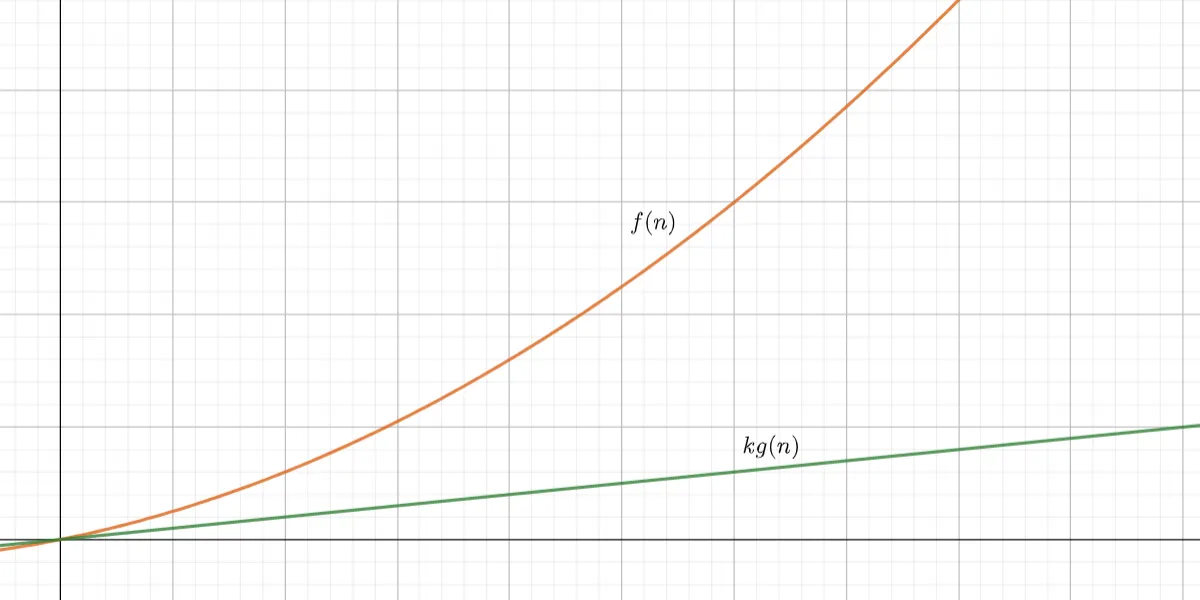
  • 形式化定义：$\exists k>0\,\exists n_{0}\,\forall n>n_{0}\colon\;|f(n)|\leq k\,g(n)$

在算法分析中，代表算法运行时间的上界，也就是最坏情况下的时间复杂度。如 $O(n^2)$ 代表算法运行时间的渐近增长速度不会超过 $n^2$.

非渐近紧确上界记号 $o$

  • 记法：$f(n)=o(g(n))$
  • 解释：$f$ 的渐近由 $g$ 主导
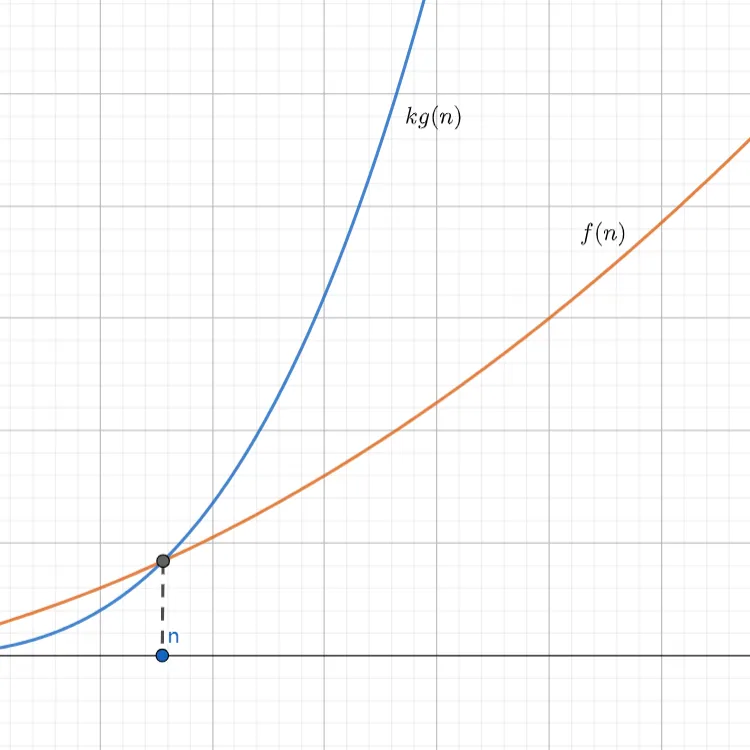
  • 形式化定义：$\forall k>0\,\exists n_{0}\,\forall n>n_{0}\colon\;|f(n)|< k\,g(n)$

$O$ 记号提供的渐近上界可以是渐近紧确的，也可以是非渐近紧确的；$o$ 记号提供的只能是非渐近紧确的。

渐近紧确：$f$ 和 $g$ 同阶，如 $n^2+n=O(n^2)$

非渐近紧确：$f$ 低于 $g$ 的阶，如 $n^2+n=o(n^3)$

渐进下界记号 $\Omega$

  • 记法：$f(n)=\Omega(g(n))$
  • 解释：$f$ 的渐近下界为 $g$
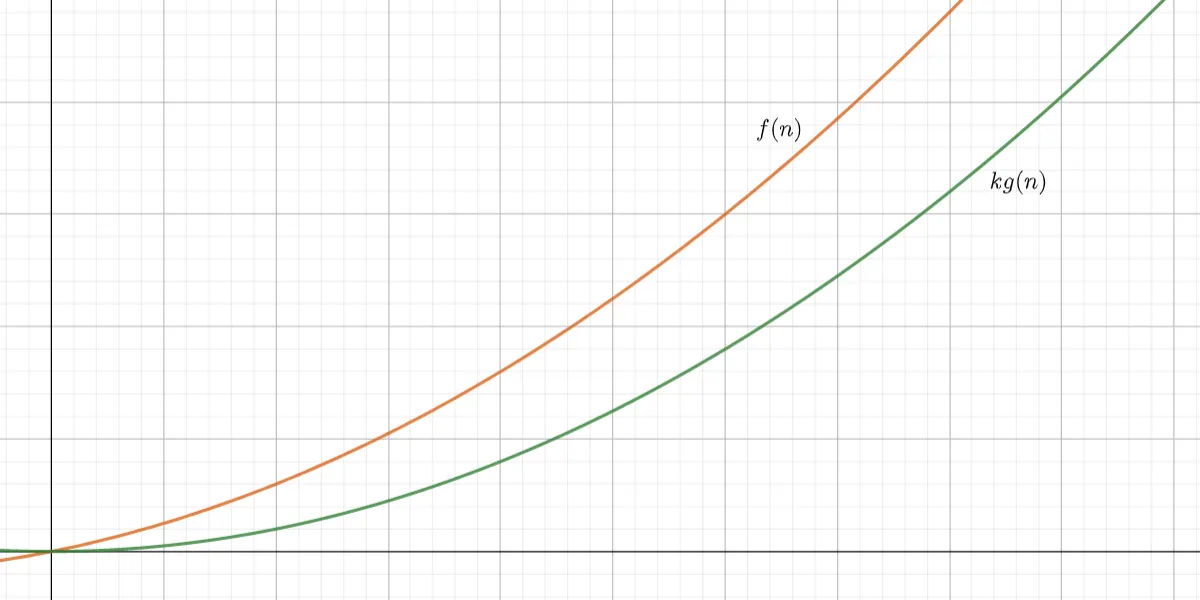
  • 形式化定义：$\exists k>0\,\exists n_{0}\,\forall n>n_{0}\colon\;f(n)\geq k\,g(n)$

在算法分析中，代表算法运行时间的下界，也就是最好情况下的时间复杂度。如 $\Omega(n^2)$ 代表算法运行时间的渐近增长速度不会低于 $n^2$.

非渐近紧确下界记号 $\omega$

  • 记法：$f(n)=\omega(g(n))$
  • 解释：$f$ 主导 $g$ 的渐近
  • 形式化定义：$\forall k>0\,\exists n_{0}\,\forall n>n_{0}\colon\;|f(n)|> k\,g(n)$

$\Omega$ 记号提供的渐近下界可以是渐近紧确的，也可以是非渐近紧确的；$\omega$ 记号提供的只能是非渐近紧确的。

渐近紧确：$f$ 和 $g$ 同阶，如 $n^2+n=\Omega(n^2)$

非渐近紧确：$f$ 高于 $g$ 的阶，如 $n^2+n=\omega(n)$

几种记号的总结

记号意义理解方式
$o$非渐近紧确上界与 $<$ 类似
$O$渐近上界与 $\leq$ 类似
$\Theta$紧确界与 $\approx$ 类似
$\Omega$渐近下界与 $\geq$ 类似
$\omega$非渐近紧确下界与 $>$ 类似

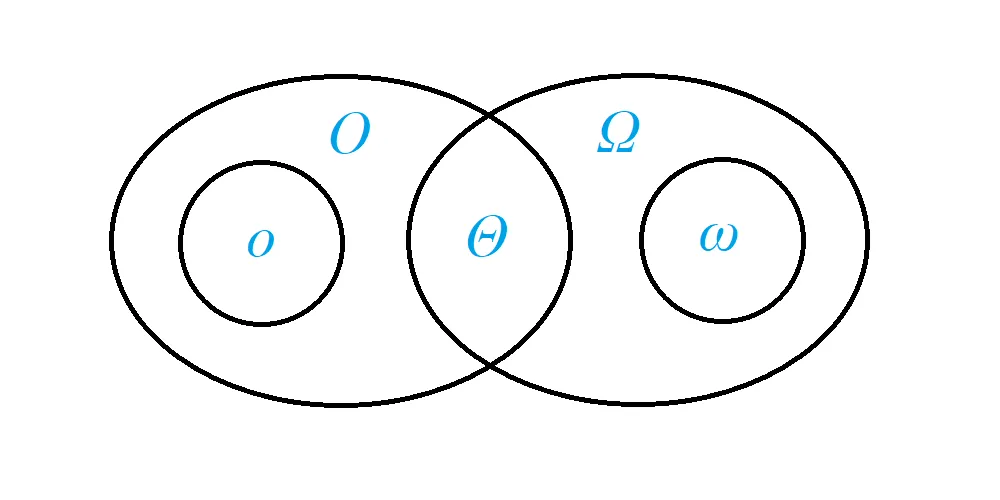
维恩图表示：

由数据范围反推算法复杂度以及算法内容——yxc

一般 ACM 或者笔试题的时间限制是 1 秒或 2 秒。
在这种情况下，C++ 代码中的操作次数控制在 $10^7\sim10^8$ 为最佳。

下面给出在不同数据范围下，代码的时间复杂度和算法该如何选择：

数据范围算法复杂度算法内容
$n\leq30$指数级别DFS + 剪枝、状态压缩 DP
$n\leq10^2$$O(n^3)$Floyd、DP、高斯消元
$n\leq10^3$$O(n^2)$, $O(n^2\log n)$DP、二分、朴素版 Dijkstra、朴素版 Prim、Bellman-Ford
$n\leq10^4$$O(n\sqrt n)$块状链表、分块、莫队
$n\leq10^5$$O(n\log n)$各种 sort、线段树、树状数组、(STL)set/map、堆、拓扑排序、Dijkstra + 堆、Prim + 堆、Kruskal、SPFA、求凸包、求半平面交、二分、CDQ 分治、整体二分、后缀数组、树链剖分、动态树
$n\leq10^6$$O(n)$, 低常数 $O(nlogn)$单调队列、 哈希、双指针扫描、并查集、KMP、AC 自动机；sort、树状数组、堆、Dijkstra、SPFA
$n\leq10^7$$O(n)$双指针扫描、KMP、AC 自动机、线性筛素数
$n\leq10^9$$O(\sqrt n)$判断质数
$n\leq10^{18}$$O(\log n)$最大公约数、快速幂、数位 DP
$n\leq10^{1000}$$O(\log^2 n)$高精度加减乘除
$n\leq10^{100000}$$O(\log n\cdot\log\log n)$ n表示位数高精度加减、FFT/NTT