题目 | Least Prefix Sum

Hello 2023

C. Least Prefix Sum

https://codeforces.com/contest/1779/problem/C

2 seconds / 256 megabytes

standard input / standard output

Problem

Baltic, a famous chess player who is also a mathematician, has an array $a_{1}, a_{2}, \dots, a_{n}$ , and he can perform the following operation several (possibly $0$ ) times:

Choose some index $i$ ( $1 \leq i \leq n$ );
multiply $a_{i}$ with $- 1$ , that is, set $a_{i} := - a_{i}$ .
Baltic's favorite number is $m$ , and he wants $a_{1} + a_{2} + \dots + a_{m}$ to be the smallest of all non-empty prefix sums. More formally, for each $k = 1, 2, \dots, n$ it should hold that

$a_{1} + a_{2} + \dots + a_{k} \geq a_{1} + a_{2} + \dots + a_{m} .$

Please note that multiple smallest prefix sums may exist and that it is only required that $a_{1} + a_{2} + \dots + a_{m}$ is one of them.

Help Baltic find the minimum number of operations required to make $a_{1} + a_{2} + \dots + a_{m}$ the least of all prefix sums. It can be shown that a valid sequence of operations always exists.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ( $1 \leq t \leq 10 000$ ). The description of the test cases follows.

The first line of each test case contains two integers $n$ and $m$ ( $1 \leq m \leq n \leq 2 \cdot 10^{5}$ ) — the size of Baltic's array and his favorite number.

The second line contains $n$ integers $a_{1}, a_{2}, \dots, a_{n}$ ( $- 10^{9} \leq a_{i} \leq 10^{9}$ ) — the array.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^{5}$ .

Output

For each test case, print a single integer — the minimum number of required operations.

Example

Input

6
4 3
-1 -2 -3 -4
4 3
1 2 3 4
1 1
1
5 5
-2 3 -5 1 -20
5 2
-2 3 -5 -5 -20
10 4
345875723 -48 384678321 -375635768 -35867853 -35863586 -358683842 -81725678 38576 -357865873

Output

1
1
0
0
3
4

Note

In the first example, we perform the operation $a_{4} := - a_{4}$ . The array becomes $[- 1, - 2, - 3, 4]$ and the prefix sums, $[a_{1}, a_{1} + a_{2}, a_{1} + a_{2} + a_{3}, a_{1} + a_{2} + a_{3} + a_{4}]$ , are equal to $[- 1, - 3, - 6, - 2]$ . Thus $a_{1} + a_{2} + a_{3} = - 6$ is the smallest of all prefix sums.

In the second example, we perform the operation $a_{3} := - a_{3}$ . The array becomes $[1, 2, - 3, 4]$ with prefix sums equal to $[1, 3, 0, 4]$ .

In the third and fourth examples, $a_{1} + a_{2} + \dots + a_{m}$ is already the smallest of the prefix sums — no operation needs to be performed.

In the fifth example, a valid sequence of operations is:

$a_{3} := - a_{3}$ ,
$a_{2} := - a_{2}$ ,
$a_{5} := - a_{5}$ .

The array becomes $[- 2, - 3, 5, - 5, 20]$ and its prefix sums are $[- 2, - 5, 0, - 5, 15]$ . Note that $a_{1} + a_{2} = - 5$ and $a_{1} + a_{2} + a_{3} + a_{4} = - 5$ are both the smallest of the prefix sums (and this is a valid solution).

题解

题意

给定一个序列 $a_{1}, a_{2}, \dots, a_{n}$ 和下标 $m$ ，通过翻转（乘 $- 1$ ）任意位，让第 $m$ 位的前缀和 $\leq$ 整个序列的所有前缀和。问最少翻转几次。

思路

对下标 $x$ 进行操作，下标 $\geq x$ 的前缀和大小关系不变

下图为前缀和的折线图，我们对 $a_{2}$ （即 $B$ 点）进行操作，即 $a_{2}$ 变成 $- a_{2}$ .

可以看到变化是 $\geq 2$ 的部分整体向下偏移了 $2 a_{2}$ ，而该部分内部的大小关系没有变化。

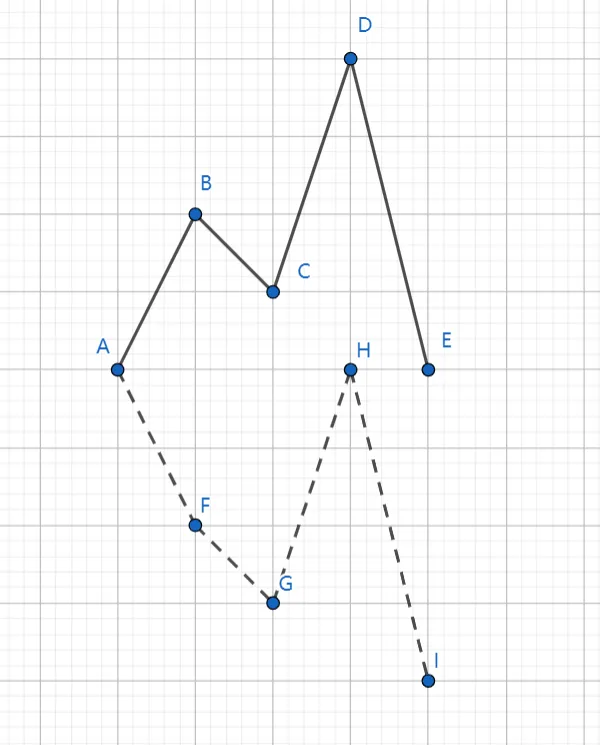
这个结论的作用是，我们对下标 $x$ 进行操作，不会改变 $\geq x$ 部分的合法性。若操作前 $\geq x$ 部分的已经符合条件，操作后也是符合条件的。

对 $> 0$ 的元素 $a_{i}$ 进行操作，能让该元素及其右侧偏移 $- 2 a_{i}$ ；

对 $< 0$ 的元素 $a_{i}$ 进行操作，能让该元素及其右侧偏移 $+ 2 a_{i}$ .

如下图，我们对 $a_{4}$ （即 $D$ 点）进行操作，可见它及其右侧向下偏移了 $2 \times 3 = 6$ .

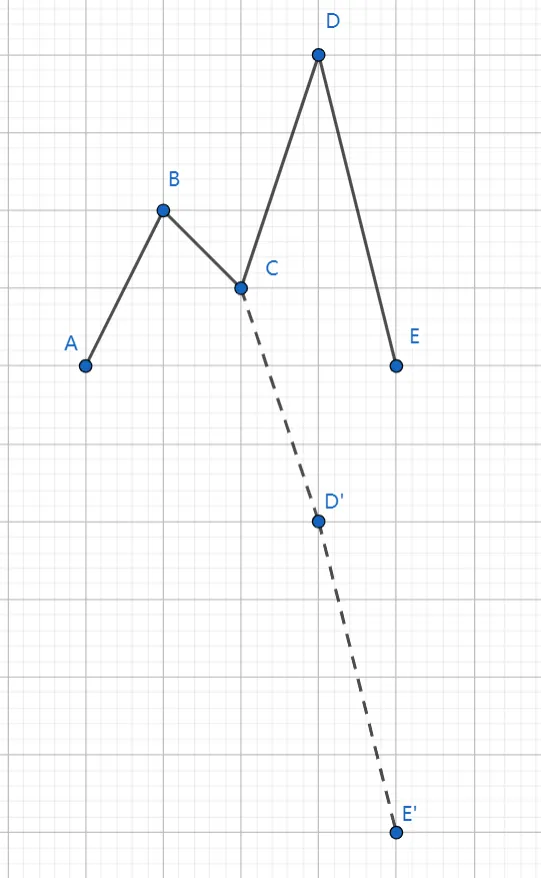
并且， $> 0$ 时，若 $a_{i}$ 越大，向下偏移量就越大； $< 0$ 时 $a_{i}$ 越小，向上偏移量最大。

由于我们要操作次数最小，根据贪心，我们肯定选的是当前的最值进行操作。（这点非常重要，我就是因为比赛时一直没想到这点，一直陷入错误的思维。没做出来这题的人很多都是这点漏掉了）

对于 $m$ 左侧的区间，如果出现不合法，则对最大的元素进行操作

从 $m$ 遍历到 $1$ ，如果发现第 $x$ 位前缀和不合法（即 $p r e s u m_{x} < p r e s u m_{m}$ ），则寻找 $(x, m]$ 中最大的元素 $a_{i}$ （一定 $> 0$ ），对其进行操作，操作数 $+ 1$ .

由于 $i < m$ ，所以操作后 $a_{m}$ 一定会受到影响而向下偏移 $2 a_{i}$ . 我们只需要更新 $p r e s u m_{m}$ 即可，因为其他的前缀和大小关系不变，我们用不上就不需要考虑了。

对于 $m$ 右侧的区间，如果出现不合法，则对最小的元素进行操作

从 $m + 1$ 遍历到 $n$ ，如果发现第 $x$ 位前缀和不合法（即 $p r e s u m_{x} < p r e s u m_{m}$ ），则寻找 $[m + 1, n]$ 中最小的元素 $a_{i}$ （一定 $< 0$ ），对其进行操作，操作数 $+ 1$ .

由于 $i < x$ ，所以操作后 $a_{x}$ 及其右侧一定会收到影响而向上偏移 $2 a_{i}$ . 我们记录一个 $o f f s e t$ 变量，即可得知右侧目前偏移了多少。

最大最小值的维护方法

使用 STL 优先队列即可实现

代码

#include <bits/stdc++.h>
#define int long long
#define endl '\n'

using namespace std;

const int MAXN = 2e5 + 10;
int n, m;
int a[MAXN], ps[MAXN];

void solve()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    for (int i = 1; i <= n; i++)
        ps[i] = ps[i - 1] + a[i];
    int psm = ps[m], cnt = 0, offset = 0;
    priority_queue<int> big_heap;
    for (int i = m; i >= 1; i--)
    {
        while (ps[i] < psm + offset)
        {
            cnt++;
            offset -= big_heap.top() * 2;
            big_heap.pop();
        }
        if (a[i] > 0)
            big_heap.push(a[i]);
    }
    priority_queue<int, vector<int>, greater<int>> small_heap;
    offset = 0;
    for (int i = m + 1; i <= n; i++)
    {
        if (a[i] < 0)
            small_heap.push(a[i]);
        while (ps[i] + offset < psm)
        {
            cnt++;
            offset -= small_heap.top() * 2;
            small_heap.pop();
        }
    }
    cout << cnt << endl;
}

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}