题目 | Grid Rotations
AtCoder Regular Contest 153
B - Grid Rotations
https://atcoder.jp/contests/arc153/tasks/arc153_b
Time Limit: $2$ sec / Memory Limit: $1024$ MB
Score : $500$ points
Problem Statement
We have a grid with $H$ rows from top to bottom and $W$ columns from left and right. Initially, the square at the $i$-th row from the top and $j$-th column from the left has a lowercase English letter $A_{i,j}$.
Let us perform $Q$ operations on this grid. In the $i$-th operation, we are given integers $a_i$ and $b_i$ such that $1\leq a_i \leq H-1$ and $1\leq b_i\leq W-1$, and do the following.
Let $R_1$, $R_2$, $R_3$, and $R_4$ be rectangular regions within the grid defined as follows:
- $R_1$ is the intersection of the top $a_i$ rows and leftmost $b_i$ columns;
- $R_2$ is the intersection of the top a_i rows and rightmost $W-b_i$ columns;
- $R_3$ is the intersection of the bottom H-a_i rows and leftmost $b_i$ columns;
- $R_4$ is the intersection of the bottom H-a_i rows and rightmost $W-b_i$ columns.
- Rotate $180$ degrees each of $R_1$, $R_2$, $R_3$, and $R_4$.
Here, a $180$-degree rotation of a rectangular region $R$ within the grid moves the character on the square at the $i$-th from the top and $j$-th column from the left in $R$ to the square at the $i$-th from the bottom and $j$-th column from the right in $R$. See also the figures for the samples.
Print the grid after all $Q$ operations.
Constraints
- $2\leq H, W$, and $HW \leq 5\times 10^5$.
- $A_{i,j}$ is a lowercase English letter.
- $1\leq Q\leq 2\times 10^5$
- $1\leq a_i\leq H - 1$
- $1\leq b_i\leq W - 1$
Input
The input is given from Standard Input in the following format:
$H$ $W$
$A_{1,1}\cdots A_{1, W}$
$\vdots$
$A_{H,1}\cdots A_{H, W}$
$Q$
$a_1$ $b_1$
$\vdots$
$a_Q$ $b_Q$
Output
Print the grid after the operations in the following format, where $B_{i,j}$ is the character on the square $(i,j)$ on the final grid.
$B_{1,1}\cdots B_{1, W}$
$\vdots$
$B_{H,1}\cdots B_{H, W}$
Sample Input 1
4 5
abcde
fghij
klmno
pqrst
1
3 3
Sample Output 1
mlkon
hgfji
cbaed
rqpts
The grid will change as follows.
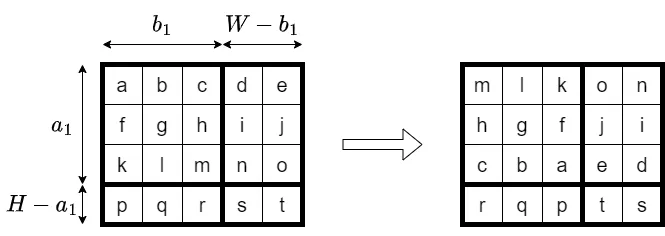
Sample Input 2
3 7
atcoder
regular
contest
2
1 1
2 5
Sample Output 2
testcon
oderatc
ularreg
The grid will change as follows.
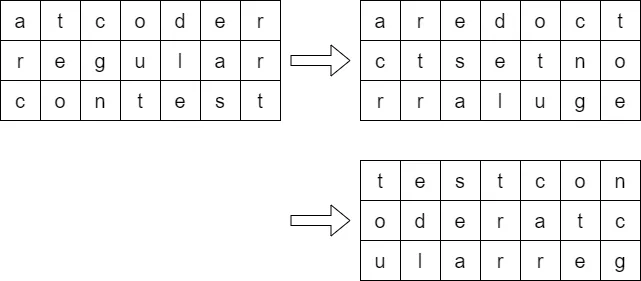
Sample Input 3
2 2
ac
wa
3
1 1
1 1
1 1
Sample Output 3
ac
wa
The grid will change as follows.

题解
同一行/列元素操作后仍在同一行/列
通过观察可以发现,题目所述操作是对整行、整列进行的。因此同一行元素操作后仍在同一行、同一列元素操作后仍在同一列,只是顺序变化了。
由此,我们可以想到,无需维护每次操作整个矩阵的值,而只用维护行列前后对应关系即可,即第 $x$ 行/列操作后变成了第 $y$ 行/列。最后输出时根据行列对应关系生成新矩阵即可。
如果使用暴力法,时间复杂度为:$O(Q\cdot(H+W))$. 根据题目要求,最坏的情况是 $H=W\approx700$,复杂度 $10^8$ 级别,会超时。由此可见,必须对行列对应关系的维护方式进行优化。
行列对应关系的特点
我们通过一个例子来解释,我们先只考虑行,因为这个问题行列是独立的:
$$ \begin{align} 初始情况:\;&12345678\\ 对第4位操作:\;&43218765\\ 对第2位操作:\;&34567812\\ 对第7位操作:\;&18765432\\ 对第3位操作:\;&78123456 \end{align} $$
此时获取还看不出规律,我们加上一些辅助:
$$ \begin{align} 初始情况:\;&\overrightarrow{12345678}|\\ 对第4位操作:\;&\overleftarrow{4321}|\overleftarrow{8765}\\ 对第2位操作:\;&\overrightarrow{345678}|\overrightarrow{12}\\ 对第7位操作:\;&\overleftarrow{1}|\overleftarrow{8765432}\\ 对第3位操作:\;&\overrightarrow{78}|\overrightarrow{123456} \end{align} $$
这样就很明显了,每次操作其实序列都是顺序的,只不过起始点发生了偏移。并且奇数次操作时为逆序,偶数次操作时为顺序。那么我们就不需要维护整个行列对应关系了,而只需要维护起始点 $1$ 就行了。最后输出时,通过起始点的位置,结合操作的次数,生成出行列对应关系,再用行列对应关系生成出新矩阵就行了。
时间复杂度为:$O(Q+HW)$,可以满足题目要求。
代码
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int H, W;
cin >> H >> W;
vector<string> A(H);
for (int i = 0; i < H; i++)
cin >> A[i];
int Q;
cin >> Q;
int start_row = 0, start_col = 0;
for (int i = 0; i < Q; i++)
{
int a, b;
cin >> a >> b;
a--, b--;
start_row = (start_row <= a) ? (a - start_row) : (H - start_row + a);
start_col = (start_col <= b) ? (b - start_col) : (W - start_col + b);
}
vector<int> row(H), col(W);
if (Q & 1)
{
for (int i = 0; i < H; i++)
row[(start_row - i + H) % H] = i;
for (int i = 0; i < W; i++)
col[(start_col - i + W) % W] = i;
}
else
{
for (int i = 0; i < H; i++)
row[(start_row + i) % H] = i;
for (int i = 0; i < W; i++)
col[(start_col + i) % W] = i;
}
for (int i = 0; i < H; i++)
{
for (int j = 0; j < W; j++)
cout << A[row[i]][col[j]];
cout << endl;
}
return 0;
}本文采用 CC BY-SA 4.0 许可,本文 Markdown 源码:Haotian-BiJi