题目 | Abs Abs Function

AtCoder Regular Contest 155

B - Abs Abs Function

https://atcoder.jp/contests/arc155/tasks/arc155_b

Time Limit: 2 sec / Memory Limit: 1024 MB

Score : $500$ points

Problem Statement

For a set $S$ of pairs of non-negative integers, and a non-negative integer $x$, let $f_S(x)$ defined as $\displaystyle f_S(x)=\min_{(a, b) \in S} \left| \left| x-a \right| - b \right|$.

We have a set $T$ of pairs of non-negative integers. Initially, $T=\lbrace (A, B)\rbrace$.

Process $Q$ queries. The $i$-th query gives you three non-negative integers $t_i$, $a_i$, and $b_i$, and asks you to do the following.

If $t_i=1$, add to $T$ the pair $(a_i, b_i)$ of non-negative integers.
If $t_i=2$, print the minimum value of $f_{T}(x)$ for a non-negative integer $x$ such that $a_i \leq x \leq b_i$.

Constraints

$1 \leq Q \leq 2 \times 10^5$
$0 \leq A,B \leq 10^{9}$
$t_i$ is $1$ or $2$.
$0 \leq a_i,b_i \leq 10^{9}$
If $t_i=2$, then $a_i \leq b_i$.
There is at least one query with $t_i=2$.
All values in the input are integers.

Input

The input is given from Standard Input in the following format:

$Q$ $A$ $B$
$t_1$ $a_1$ $b_1$
$t_2$ $a_2$ $b_2$
$\vdots$
$t_Q$ $a_Q$ $b_Q$

Output

For each query with $t_i=2$ in the given order, print the answer in its own line.

Sample Input 1

4 0 5
1 3 11
2 7 8
1 8 2
2 8 9

Sample Output 1

2
1

In the fourth query, $T=\lbrace(0, 5), (3, 11), (8, 2) \rbrace$. In $8 \leq x \leq 9$, $f_T(x)$ takes the minimum value $f_T(9)=1$ at $x=9$.

Sample Input 2

2 1 2
1 2 3
2 2 6

Sample Output 2

0

Sample Input 3

20 795629912 123625148
2 860243184 892786970
2 645778367 668513124
1 531411849 174630323
1 635062977 195695960
2 382061637 411843651
1 585964296 589553566
1 310118888 68936560
1 525351160 858166280
2 395304415 429823333
2 583145399 703645715
2 97768492 218377432
1 707220749 459967102
1 210842017 363390878
2 489541834 553583525
2 731279777 811513313
1 549864943 493384741
1 815378318 826084592
2 369622093 374205455
1 78240781 821999998
2 241667193 243982581

Sample Output 3

26468090
3491640
25280111
9543684
0
22804896
20649370
19245624
4849993
484865

题解

核心思路

将函数 $p(x):=\left|\left|x-a\right|-b\right|$ 做变形：

$$ \begin{align} p(x)&=\left|\left|x-a\right|-b\right|\\ &=\min\left\{\left|x-(a+b)\right|,\left|x-(a-b)\right|\right\} \end{align} $$

函数图像如下：

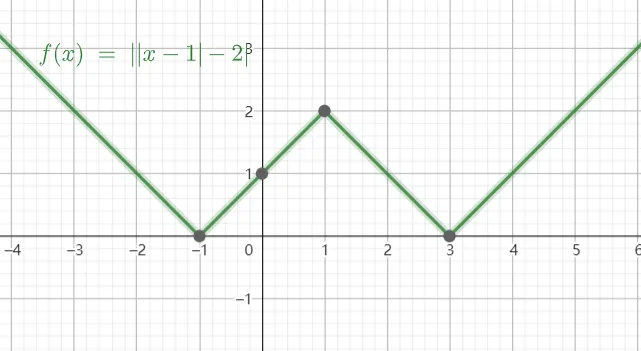
通过变形，该函数的最小值点就很明确了，就是 $a+b$ 和 $a-b$，最小值为 $0$.

完整思路

我们将每对 $(a,b)$ 对应的函数 $p(x)$ 的最小值点记录下来，存在集合 $S$ 中。即把 $a+b$ 与 $a-b$ 储存在 $S$ 内。

当要输出答案时，$x$ 需要满足 $a\leq x\leq b$：

若 $\exists t\in S,\;a\leq t\leq b$，那么 $x$ 取 $t$ 即可令某一个 $\left|\left|x-a\right|-b\right|=0$，取最小值后 $f_S(x)=0$
若 $\forall t\in S,\;t<a\ 或\ t>b$，那么 $x$ 取距离 $a$ 或距离 $b$ 最近的一个 $t$ 即可令 $\left|\left|x-a\right|-b\right|$ 最小，$f_S(x)=\min\{a-t_1,t_2-b\}$

代码

#include <bits/stdc++.h>
#define endl '\n'
#define int long long

using namespace std;

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int Q, A, B;
    cin >> Q >> A >> B;
    set<int> s;
    s.insert(A + B);
    s.insert(A - B);
    while (Q--)
    {
        int t, a, b;
        cin >> t >> a >> b;
        if (t == 1)
        {
            s.insert(a + b);
            s.insert(a - b);
        }
        else
        {
            auto it = s.lower_bound(a);
            if (it == s.end())
                cout << a - *s.rbegin() << endl;
            else if (*it <= b)
                cout << 0 << endl;
            else if (it == s.begin())
                cout << *it - b << endl;
            else
                cout << min(*it - b, a - *prev(it)) << endl;
        }
    }
    return 0;
}