Educational Codeforces Round 149 (Rated for Div. 2)

D. Bracket Coloring

https://codeforces.com/contest/1837/problem/D

2 seconds / 512 megabytes

standard input / standard output

Problem

A regular bracket sequence is a bracket sequence that can be transformed into a correct arithmetic expression by inserting characters "1" and "+" between the original characters of the sequence. For example:

  • the bracket sequences "()()" and "(())" are regular (the resulting expressions are: "(1)+(1)" and "((1+1)+1)");
  • the bracket sequences ")(", "(" and ")" are not.
    A bracket sequence is called beautiful if one of the following conditions is satisfied:
  • it is a regular bracket sequence;
  • if the order of the characters in this sequence is reversed, it becomes a regular bracket sequence.

For example, the bracket sequences "()()", "(())", ")))(((", "))()((" are beautiful.

You are given a bracket sequence $s$. You have to color it in such a way that:

  • every bracket is colored into one color;
  • for every color, there is at least one bracket colored into that color;
  • for every color, if you write down the sequence of brackets having that color in the order they appear, you will get a beautiful bracket sequence.

Color the given bracket sequence $s$ into the minimum number of colors according to these constraints, or report that it is impossible.

Input

The first line contains one integer $t$ ($1 \le t \le 10^4$) — the number of test cases.

Each test case consists of two lines. The first line contains one integer $n$ ($2 \le n \le 2 \cdot 10^5$) — the number of characters in $s$. The second line contains $s$ — a string of $n$ characters, where each character is either "(" or ")".

Additional constraint on the input: the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$.

Output

For each test case, print the answer as follows:

  • if it is impossible to color the brackets according to the problem statement, print $-1$;
  • otherwise, print two lines. In the first line, print one integer $k$ ($1 \le k \le n$) — the minimum number of colors. In the second line, print $n$ integers $c_1, c_2, \dots, c_n$ ($1 \le c_i \le k$), where $c_i$ is the color of the $i$-th bracket. If there are multiple answers, print any of them.

Example

Input

4
8
((())))(
4
(())
4
))((
3
(()

Output

2 2 2 1 2 2 2 1
1
1 1 1 1
1
1 1 1 1
-1

题解

重点一：何时无解

这一点还是比较容易发现的，即 ( 的数目与 ) 的数目相同时有解，不同时无解。

因为对于合法的括号组，正括号与反括号的数量一定相同，这点说明数量不同时无解。

对于数量相同时是否一定有解这个问题，我们可以构造一个简单的合法解：随意挑选一对 ( 和 )，涂上相同的颜色，再挑选出一对，涂上和之前不一样的颜色，重复这个过程。最后所有括号一定会全部被拆分为单独的括号对，这种解一定合法（但是明显不是最优）

重点二：颜色数量

为了让问题更直观，我们将 ( 转换为 $+1$，将 ) 转换为 $-1$，那么序列 (()(())) 可以表示为：

我们可以发现，每层都可以用蓝色箭头连接一对括号，将每对括号匹配上。因此上述序列已经是合法的括号序列，可以全部涂成一种颜色。考察另外一个序列 )())()((，它可以表示为：

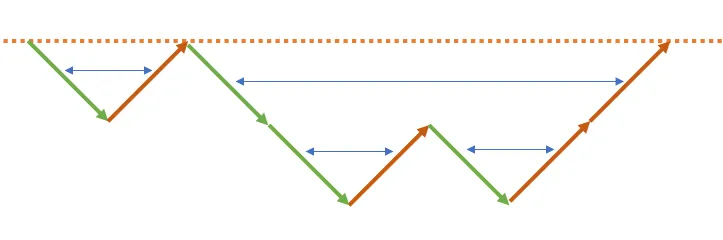
我们可以发现，每层的蓝色箭头仍然可以把每对括号匹配上，但是这次括号的顺序反了，不过它的逆序括号顺序就正了。因此也是合法的括号序列，可以全部涂成同一种颜色。综上，对于全部 $\leq0$ 和全部 $\geq0$ 的情况，可以全部涂成同一种颜色。接下来需要讨论的就是既有 $\leq0$ 也有 $\geq0$ 的情况：

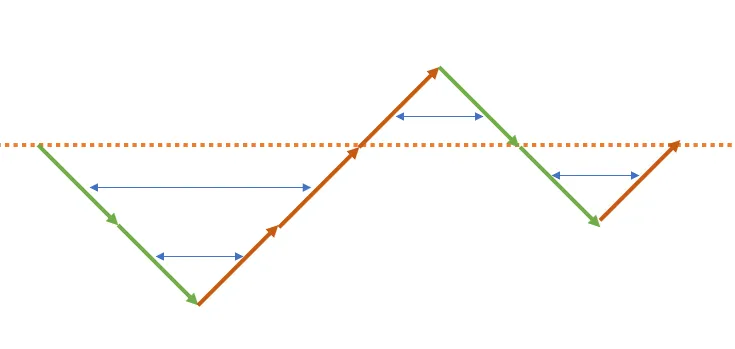
对于 $\leq0$ 的情况，我们需要逆序；对于 $\geq0$ 的情况，我们不能逆序：因此这两种情况不可共存。那么我们可以将 $\leq0$ 的情况涂上一种颜色，$\geq0$ 的情况涂上另一种颜色，这样就能把二者隔离开了，并且两者都是合法的序列。

代码

#include <bits/stdc++.h>
#define endl '\n'

using namespace std;

void solve()
{
    int n;
    cin >> n;
    string s;
    cin >> s;
    vector<int> a(n + 1);
    bool pos = false, neg = false;
    for (int i = 0; i < n; i++)
    {
        if (s[i] == '(')
            a[i + 1] = a[i] + 1;
        else
            a[i + 1] = a[i] - 1;
        if (a[i] > 0)
            pos = true;
        if (a[i] < 0)
            neg = true;
    }
    if (a.back() != 0)
    {
        cout << -1 << endl;
        return;
    }
    if (!(pos && neg))
    {
        cout << 1 << endl;
        for (int i = 0; i < n; i++)
            cout << 1 << ' ';
        cout << endl;
    }
    else
    {
        cout << 2 << endl;
        for (int i = 0; i < n; i++)
        {
            if (a[i] >= 0 && a[i + 1] >= 0)
                cout << 1 << ' ';
            else
                cout << 2 << ' ';
        }
        cout << endl;
    }
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}