支持向量机 (Support Vector Machine, SVM)：支持向量机在高维或无限维空间中构造超平面或超平面集合，其可以用于分类、回归或其他任务。直观来说，分类边界距离最近的训练资料点越远越好，因为这样可以缩小分类器的泛化误差。

1. 定义

更正式地来说，支持向量机在高维或无限维空间中构造超平面或超平面集合，其可以用于分类、回归或其他任务。直观来说，分类边界距离最近的训练资料点越远越好，因为这样可以缩小分类器的泛化误差。（来源：维基百科，使用 CC BY-SA 3.0 协议）

对于二维二分类问题如下：

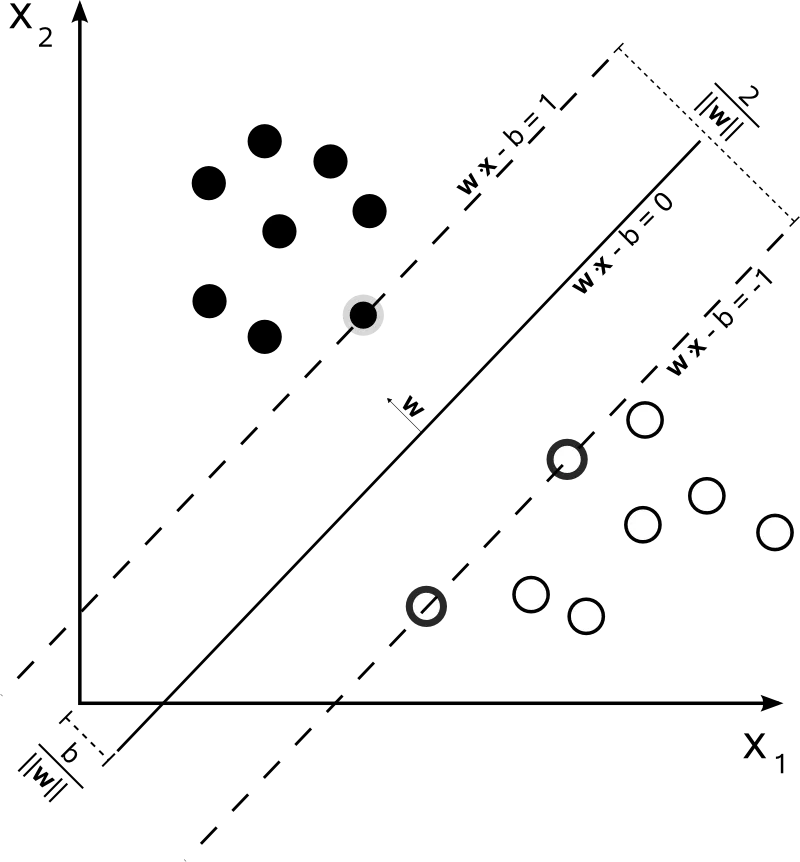
（来源：维基百科，使用 CC BY-SA 3.0 协议）

当我们来对两种样本人工分类的时候，一定是想找到间隔最宽的一个空隙划开，因为我们感觉这样的分类效果最好。

支持向量机和人的思维一致，就是要找到一个分类超平面 $w \cdot x - b = 0$ ，并且希望该超平面支持向量的间隔越大越好，因为这样可以减小在测试集上的泛化误差。

支持向量是训练数据集中最靠近分类超平面的点。

2. 线性 SVM

2.1 硬间隔

2.1.1 间隔的定义

SVM 的核心就是间隔越大越好，那么我们首先要找到间隔的数学表达。

平面中点 $(x_{0}, y_{0})$ 到直线的 $a x + b y + c = 0$ 距离公式：

$\begin{matrix} (a.1) & d = \frac{| a x_{0} + b y_{0} + c |}{\sqrt{a^{2} + b^{2}}} \end{matrix}$

有些资料向量相乘写成 $w \cdot x$ ，有些资料写成 $w^{T} x$ ，二者实际是一样的。因为前者是点乘（内积），后者是叉乘（外积）。

将上式推广到多维空间中一样成立。对于超平面 $w^{T} x + b = 0$ ，点 $x$ 到其的距离为：

$\begin{matrix} (a.2) & d = \frac{| w^{T} x + b |}{‖ w ‖} \end{matrix}$

$‖ x ‖$ 为 $x$ 的二范数（下标 2 可省略），其定义是： $‖ x ‖_{2} = \sqrt{\sum_{i = 1}^{n} x_{i}^{2}}$

我们将 $\pm 1$ 作为每个样本点的类别标签，如果样本可以线性可分，那么一定存在分类超平面满足：

$\begin{matrix} (a.3) & {\begin{cases} w^{T} x_{i} + b > 0, & y_{i} = 1 \\ w^{T} x_{i} + b < 0, & y_{i} = - 1 \end{cases} \end{matrix}$

这个条件实际上非常弱，它相当于只规定了分类超平面能把两种样本点隔开，没有任何对间隔的限制。

为了引入间隔，我们假设支持向量到分类超平面的距离为 $d$ ，那么我们要求分类超平面：

$\begin{matrix} (a.4) & {\begin{cases} if y_{i} = 1, & then \frac{w^{T} x_{i} + b}{‖ w ‖} \geq d \\ if y_{i} = - 1, & then \frac{w^{T} x_{i} + b}{‖ w ‖} \leq - d \end{cases} \end{matrix}$

这样表达式中终于包含了间隔。接下来，我们对上式两边除以 $d$ ：

$\begin{matrix} (a.5) & {\begin{cases} if y_{i} = 1, & then \frac{w^{T} x_{i} + b}{‖ w ‖ d} \geq 1 \\ if y_{i} = - 1, & then \frac{w^{T} x_{i} + b}{‖ w ‖ d} \leq - 1 \end{cases} \end{matrix}$

由于 $‖ w ‖$ 和 $d$ 都是标量，因此除以分母相当于对该超平面进行缩放，实际上超平面是没有变化的。

就像 $2 x + 4 y = 0$ 缩放为 $x + 2 y = 0$ ，两个式子表示的仍然是同一条直线。

因此为了式子简单，我们直接忽略掉缩放的值：

$\begin{matrix} (a.6) & {\begin{cases} if y_{i} = 1, & then w^{T} x_{i} + b \geq 1 \\ if y_{i} = - 1, & then w^{T} x_{i} + b \leq - 1 \end{cases} \end{matrix}$

对于支持向量 $x_{i}$ ，其满足：

$\begin{matrix} (a.7) & | w^{T} x_{i} + b | = 1 \end{matrix}$

那么支持向量与分类超平面的距离为：

$\begin{matrix} (a.8) & d = \frac{| w^{T} x_{i} + b |}{‖ w ‖} = \frac{1}{‖ w ‖} \end{matrix}$

由于间隔有两侧，那么间隔的距离为：

$\begin{matrix} (a.9) & d = \frac{2}{‖ w ‖} \end{matrix}$

2.1.2 待求解的问题

获得了间隔的表达式，支持向量机要求解的问题就可以用形式化的语言表达：

$\begin{matrix} (b.1) & \begin{aligned} max_{w, b} \frac{2}{‖ w ‖} \\ s . t . y_{i} (w^{T} x_{i} + b) \geq 1 \end{aligned} \end{matrix}$

这里第二行公式把 $y_{i}$ 乘到左边去了，是为了表达式的简洁。实际上这一行表达的含义与式 $(a.6)$ 是一模一样的。

我们习惯求最小化问题，因此将以上问题分子分母颠倒，等价转换为：

$\begin{matrix} (b.2) & \begin{aligned} min_{w, b} \frac{1}{2} ‖ w ‖^{2} \\ s . t . y_{i} (w^{T} x_{i} + b) \geq 1 \end{aligned} \end{matrix}$

其中，加平方是为了求导时正好能把前面的 $1 / 2$ 消去。

2.1.3 前置知识

可以先看下一节求解的过程，过程中遇到了对应的方法后再看这一节。

2.1.3.1 拉格朗日乘子法

对于不等式约束优化问题：

$\begin{aligned} min_{x} f (x) \\ \begin{aligned} s . t . & h_{i} (x) = 0, i = 1, 2, . . ., m \\ g_{j} (x) < 0, j = 1, 2, . . ., n \end{aligned} \end{aligned}$

转化为其对应的无约束的拉格朗日函数：

$L (x, α, β) = f (x) + \sum_{i = 1}^{m} α_{i} h_{i} (x) + \sum_{j = 1}^{n} β_{j} g_{j} (x)$

要满足 KKT 条件：

$\begin{aligned} (1) & \frac{\partial L (x, α, β)}{\partial x} & = 0 \\ (2) & β_{j} g_{j} (x) & = 0, j = 1, 2, . . ., n \\ (3) & h_{i} (x) & = 0, i = 1, 2, . . ., m \\ (4) & g_{j} (x) & \leq 0, j = 1, 2, . . ., n \\ (5) & β_{j} & \geq 0, j = 1, 2, . . ., n \end{aligned}$

其中：

拉格朗日取得可行解的必要条件
松弛互补条件
初始的约束条件
初始的约束条件
不等式约束的拉格朗日乘子需满足的条件

2.1.3.2 拉格朗日对偶

对于原问题：

$p^{*} = min_{x} max_{α, β; β_{i} \geq 0} L (x, α, β)$

它的对偶问题为：

$d^{*} = max_{α, β; β_{i} \geq 0} min_{x} L (x, α, β)$

定义以下式子：

$\begin{aligned} f (α, β) & = min_{x} L (x, α, β) \\ d^{*} & = max_{α, β; β_{i} \geq 0} f (α, β) = max_{α, β; β_{i} \geq 0} min_{x} L (x, α, β) \\ g (x) & = max_{α, β; β_{i} \geq 0} L (x, α, β) \\ p^{*} & = min_{x} g (x) = min_{x} max_{α, β; β_{i} \geq 0} L (x, α, β) \end{aligned}$

我们可以写出如下不等式：

$f (α, β) = min_{x} L (x, α, β) \leq L (x, α, β) \leq max_{α, β; β_{i} \geq 0} L (x, α, β) = g (x)$

再进一步转换到 $d^{*}$ 与 $p^{*}$ 上：

$d^{*} = max_{α, β; β_{i} \geq 0} f (α, β) \leq min_{x} g (x) = p^{*}$

综上，我们可以得到原问题 $p^{*}$ 和对偶问题 $d^{*}$ 的最优解的关系：

$d^{*} \leq p^{*}$

2.1.3.3 SMO 算法

SMO (Sequential Minimal Optimization) 算法的基本步骤：

选取一对需要更新的变量 $α_{i}$ 与 $α_{j}$
固定 $α_{i}$ 与 $α_{j}$ 以外的参数，求解出更新后的 $α_{i}$ 与 $α_{j}$

一直循环以上两个步骤，直到收敛。

对于选取的 $α_{i}$ 与 $α_{j}$ ，可以使用随机选取的方法，但是该方法收敛速度较慢。更优的方法是选取最不满足 KKT 条件的参数，这样更新时收敛速度会更快。

2.1.4 求解支持向量机

2.1.4.1 问题转换

由拉格朗日乘子法，我们列出拉格朗日函数：

$L (w, b, α) = \frac{1}{2} ‖ w ‖^{2} + \sum_{i = 1}^{m} α_{i} (1 - y_{i} (w^{T} x_{i} + b))$

其中 $α_{i} \geq 0$ ，为拉格朗日乘子； $m$ 为样本点的数量。

我们知道， $1 - w^{T} x_{i} + b \leq 0$ ，因此式子后半段的求和项一定 $\leq 0$ ，那么 $L (w, b, α)$ 的最大值为 $\frac{1}{2} ‖ w ‖^{2}$ 即原问题：

$max_{α} L (w, b, α) = \frac{1}{2} ‖ w ‖^{2}$

我们要求的是原问题的最小值，因此问题转换为：

$min_{w, b} max_{α} L (w, b, α)$

该问题不好求解，因此使用拉格朗日对偶法转换为对偶问题，我们求出对偶问题的最大值，便是原问题的下界：

$max_{α} min_{w, b} L (w, b, α)$

2.1.4.2 求解问题

第一步，求解内层问题：

$\begin{matrix} (e.1) & min_{w, b} L (w, b, α) = min_{w, b} \frac{1}{2} ‖ w ‖^{2} + \sum_{i = 1}^{m} α_{i} (1 - y_{i} (w^{T} x_{i} + b)) \end{matrix}$

首先对 $w$ 与 $b$ 求偏导，并算出偏导为 $0$ 时的解：

$\begin{matrix} (e.2) & \begin{aligned} {\begin{cases} \frac{\partial L (w, b, α)}{\partial w} = w - \sum_{i = 1}^{m} α_{i} y_{i} x_{i} = 0 \\ \frac{\partial L (w, b, α)}{\partial b} = \sum_{i = 1}^{m} α_{i} y_{i} = 0 \end{cases} \\ \Rightarrow & {\begin{cases} w = \sum_{i = 1}^{m} α_{i} y_{i} x_{i} \\ \sum_{i = 1}^{m} α_{i} y_{i} = 0 \end{cases} \end{aligned} \end{matrix}$

将上式的解带入式 $(18)$ ，即可得到内层问题的解如下，我们令该结果为 $L (α)$ ：

$\begin{matrix} (e.3) & L (α) = min_{w, b} L (w, b, α) = \sum_{i = 1}^{m} α_{i} - \frac{1}{2} \sum_{i = 1}^{m} \sum_{j = 1}^{m} α_{i} α_{j} y_{i} y_{j} x_{i}^{T} x_{j} \end{matrix}$

我们发现还有个条件 $\sum_{i = 1}^{m} α_{i} y_{i} = 0$ 还没用上，它将会在后续作为约束条件使用。

另外，我们令要计算的分割超平面为 $g (x) = w^{T} x + b$ ，将 $w$ 的值代入后得到：

$\begin{matrix} (e.4) & g (x) = \sum_{i = 1}^{m} α_{i} y_{i} x_{i}^{T} x + b \end{matrix}$

第二步，求解外层问题：

$\begin{matrix} (e.5) & \begin{aligned} max_{α} L (α) = max_{α} \sum_{i = 1}^{m} α_{i} - \frac{1}{2} \sum_{i = 1}^{m} \sum_{j = 1}^{m} α_{i} α_{j} y_{i} y_{j} x_{i}^{T} x_{j} \\ s . t . \sum_{i = 1}^{m} α_{i} y_{i} = 0, α_{i} \geq 0 \end{aligned} \end{matrix}$

我们习惯求最小值，因此给上述问题乘上一个 $- 1$ 转换成等价问题：

$\begin{matrix} (e.6) & \begin{aligned} min_{α} L (α) = min_{α} \frac{1}{2} \sum_{i = 1}^{m} \sum_{j = 1}^{m} α_{i} α_{j} y_{i} y_{j} x_{i}^{T} x_{j} - \sum_{i = 1}^{m} α_{i} \\ s . t . \sum_{i = 1}^{m} α_{i} y_{i} = 0, α_{i} \geq 0 \end{aligned} \end{matrix}$

该问题还需要满足 KKT 条件：

$\begin{matrix} (e.7) & {\begin{cases} α_{i} \geq 0 \\ y_{i} (w^{T} x_{i} + b) - 1 \geq 0 \\ α_{i} (y_{i} (w^{T} x_{i} + b) - 1) = 0 \end{cases} \end{matrix}$

对于该问题，我们共有 $m$ 个 $α_{i}$ 等待优化，这个量实在是太大了，不可能同时进行优化求解。使用 SMO 算法可以解决这个问题。

第三步，使用 SMO 求解外层问题：

不妨设我们选择要优化的变量为 $α_{1}$ 与 $α_{2}$ ，问题可以写为：

$\begin{matrix} (e.8) & \begin{aligned} \begin{aligned} min_{α_{1}, α_{2}} L (α_{1}, α_{2}) & = min_{α_{1}, α_{2}} \frac{1}{2} α_{1}^{2} x_{1}^{T} x_{1} + \frac{1}{2} α_{2}^{2} x_{2}^{T} x_{2} + α_{1} α_{2} y_{1} y_{2} x_{1}^{T} x_{2} \\ - α_{1} - α_{2} + α_{1} y_{1} \sum_{i = 3}^{m} y_{i} α_{i} x_{i}^{T} x_{1} + α_{2} y_{2} \sum_{i = 3}^{m} y_{i} α_{i} x_{i}^{T} x_{2} \end{aligned} \\ s . t . α_{1} y_{1} + α_{2} y_{2} = - \sum_{i = 3}^{m} α_{i} y_{i}, α_{i} \geq 0 \end{aligned} \end{matrix}$

注意上式的前两项没有 $y_{i}$ 了，因为 $y_{i} = \pm 1$ ，所以 $y_{i}^{2} = 1$ 可以直接省略。另外由于变量相当于只剩 $α_{1}$ 和 $α_{2}$ ，因此后面的双层连加变成了两个单层连加。下面该技巧也会用到多次，也会反向用到。

上式的约束条件可以进行变形：

$\begin{matrix} (e.9) & \begin{aligned} α_{1} y_{1} + α_{2} y_{2} = - \sum_{i = 3}^{m} α_{i} y_{i} \\ \Rightarrow & α_{1} = (- \sum_{i = 3}^{m} α_{i} y_{i} - α_{2} y_{2}) y_{1} \end{aligned} \end{matrix}$

其中除了 $α_{1}$ 与 $α_{2}$ 之外的其他变量全部都是已知的，因此 $α_{1}$ 与 $α_{2}$ 之间存在确定的关系。如果知道了二者其一，另一个也可以直接计算得到。因此，上面两个变量的优化问题实际上是一个变量的优化问题，完全可以将另一个变量代入替换。

为了式子简洁，我们令：

$\begin{matrix} (e.10) & \begin{aligned} f & = - \sum_{i = 3}^{m} α_{i} y_{i} = α_{1} y_{1} + α_{2} y_{2} \\ v_{i} & = \sum_{j = 3}^{m} y_{j} α_{j} x_{j}^{T} x_{i} = g (x_{i}) - \sum_{j = 1}^{2} y_{j} α_{j} x_{j}^{T} x_{i} - b \end{aligned} \end{matrix}$

通过式 $(e.9)$ 将式 $(e.8)$ 中的所有 $α_{1}$ 替换为 $α_{2}$ ，另外使用式 $(e.10)$ 的第二个等号前半段化简式 $(e.8)$ 中的表示方法（第二个等号后半段将在后续操作中用到），可以得到：

$\begin{matrix} (e.11) & \begin{aligned} \begin{aligned} min_{α_{2}} L (α_{2}) & = min_{α_{2}} \frac{1}{2} (f - α_{2} y_{2})^{2} x_{1}^{T} x_{1} + \frac{1}{2} α_{2}^{2} x_{2}^{T} x_{2} + (f - α_{2} y_{2}) α_{2} y_{2} x_{1}^{T} x_{2} \\ - (f - α_{2} y_{2}) y_{1} - α_{2} + (f - α_{2} y_{2}) v_{1} + α_{2} y_{2} v_{2} \end{aligned} \\ s . t . α_{i} \geq 0 \end{aligned} \end{matrix}$

此时，整个式子已经只剩 $α_{2}$ 这一个参数了，我们终于可以对它求偏导并置为 $0$ 得到结果了：

$\begin{matrix} (e.12) & \begin{aligned} \frac{\partial L (α_{2})}{\partial α_{2}} & = α_{2} x_{1}^{T} x_{1} - f y_{2} x_{1}^{T} x_{1} + α_{2} x_{2}^{T} x_{2} - f y_{2} x_{1}^{T} x_{2} - 2 α_{2} x_{1}^{T} x_{2} + y_{1} y_{2} - 1 - y_{2} v_{1} + y_{2} v_{2} = 0 \\ \Rightarrow α_{2} (x_{1}^{T} x_{1} + x_{2}^{T} x_{2} - 2 x_{1}^{T} x_{2}) = y_{2} (f x_{1}^{T} x_{1} - f x_{1}^{T} x_{2} - y_{1} + y_{2} + v_{1} - v_{2}) \end{aligned} \end{matrix}$

此时这个式子已经能用来计算结果了，但是还不够简单，编程实现比较麻烦，我们可以进一步进行化简。

首先注意到式 $(28)$ 的后半段， $f$ 和 $v_{i}$ 其实可以转化成关于 $α_{1}, α_{2}$ 的式子，为了区分新算出来的 $α$ ，我们将 $f$ 和 $v_{i}$ 里的记作 $α_{1}^{o l d}, α_{2}^{o l d}$ .同时，我们令损失值 $E_{i}$ 为预测值与实际值的差：

$\begin{matrix} (e.13) & E_{i} = g (x_{i}) - y_{i} = \sum_{i = j}^{m} α_{j} y_{j} x_{j}^{T} x_{i} + b - y_{i} \end{matrix}$

将 $(e.10)$ 的后半段与 $(e.13)$ 代入 $(e.12)$ ，即可得到以下式子：

$\begin{matrix} (e.14) & \begin{aligned} α_{2}^{n e w u n c} (x_{1}^{T} x_{1} + x_{2}^{T} x_{2} - 2 x_{1}^{T} x_{2}) \\ = & y_{2} (f x_{1}^{T} x_{1} - f x_{1}^{T} x_{2} - y_{1} + y_{2} + v_{1} - v_{2}) \\ = & y_{2} ((α_{1}^{o l d} y_{1} + α_{2}^{o l d} y_{2}) x_{1}^{T} x_{1} - (α_{1}^{o l d} y_{1} + α_{2}^{o l d} y_{2}) x_{1}^{T} x_{2} - y_{1} + y_{2} \\ + g (x_{1}) - y_{1} α_{1}^{o l d} x_{1}^{T} x_{1} - y_{2} α_{2}^{o l d} x_{2}^{T} x_{1} - b \\ - g (x_{2}) + y_{1} α_{1}^{o l d} x_{1}^{T} x_{2} + y_{2} α_{2}^{o l d} x_{2}^{T} x_{2} + b) \\ = & y_{2} (α_{2}^{o l d} y_{2} x_{1}^{T} x_{1} + α_{2}^{o l d} y_{2} x_{2}^{T} x_{2} - 2 α_{2}^{o l d} y_{2} x_{1}^{T} x_{2} + E_{1} - E_{2}) \\ = & α_{2}^{o l d} x_{1}^{T} x_{1} + α_{2}^{o l d} y x_{2}^{T} x_{2} - 2 α_{2}^{o l d} y x_{1}^{T} x_{2} + y_{2} (E_{1} - E_{2}) \\ = & α_{2}^{o l d} (x_{1}^{T} x_{1} + x_{2}^{T} x_{2} - 2 x_{1}^{T} x_{2}) + y_{2} (E_{1} - E_{2}) \end{aligned} \end{matrix}$

令 $η = x_{1}^{T} x_{1} + x_{2}^{T} x_{2} - 2 x_{1}^{T} x_{2}$ ，将上式左右同除以 $η$ 得到：

$\begin{matrix} (e.15) & α_{2}^{n e w u n c} = α_{2}^{o l d} + \frac{y_{2} (E_{1} - E_{2})}{η} \end{matrix}$

如此，我们将式 $(e.12)$ 化简得到了非常优美的新式子，编程实现时更加简单。

上面求出来的答案并不是最终答案，我们还需要注意到约束条件 $α_{i} \geq 0$ ，我们计算得到的 $α_{1}$ 和 $α_{2}$ 都要满足该条件。

对 $y_{1}$ 与 $y_{2}$ 的符号进行分类讨论：

$y_{1} = y_{2}$

由式 $(e.10)$ ，我们不关心符号，因此将符号并入 $t$ 中得到：

$\begin{aligned} y_{1} α_{1} + y_{2} α_{2} = f \\ \Rightarrow & α_{1} + α_{2} = t \end{aligned}$

由于 $α_{1} \geq 0, α_{2} \geq 0$ 可知：

$0 \leq α_{2}^{n e w} \leq t = α_{1}^{o l d} + α_{2}^{o l d}$

由此，我们可以将 $α_{2}^{n e w u n c}$ 剪辑：

$α_{2}^{n e w} = {\begin{cases} α_{1}^{o l d} + α_{2}^{o l d}, & α_{1}^{o l d} + α_{2}^{o l d} < α_{2}^{n e w u n c} \\ α_{2}^{n e w u n c}, & 0 \leq α_{2}^{n e w u n c} \leq α_{1}^{o l d} + α_{2}^{o l d} \\ 0, & α_{2}^{n e w u n c} < 0 \end{cases}$

$y_{1} \neq y_{2}$

由式 $(e.10)$ ，我们不关心符号，因此将符号并入 $t$ 中得到：

$\begin{aligned} y_{1} α_{1} + y_{2} α_{2} = f \\ \Rightarrow & α_{2} - α_{1} = t \end{aligned}$

由于 $α_{1} \geq 0, α_{2} \geq 0$ 可知：

$0 \leq α_{2}^{n e w} \leq t = α_{2}^{o l d} - α_{1}^{o l d}$

由此，我们可以将 $α_{2}^{n e w u n c}$ 剪辑：

$α_{2}^{n e w} = {\begin{cases} α_{1}^{o l d} + α_{2}^{o l d}, & α_{2}^{o l d} - α_{1}^{o l d} < α_{2}^{n e w u n c} \\ α_{2}^{n e w u n c}, & 0 \leq α_{2}^{n e w u n c} \leq α_{2}^{o l d} - α_{1}^{o l d} \\ 0, & α_{2}^{n e w u n c} < 0 \end{cases}$

2.2 软间隔

2.2.1 软间隔的定义

上述硬间隔 SVM 考虑的情况比较理想，样本点不存在噪音。如果样本点存在噪音，将会对硬间隔 SVM 造成干扰，导致泛化能力下降。或者样本点线性不可分，硬间隔 SVM 就无法处理。

在硬间隔 SVM 里，我们要求两类样本点一定分别分布于分割超平面两侧，即样本点一定被分割超平面正确分割。在软间隔 SVM 里，我们降低这个要求，允许样本点被错误分类。

如果样本点能随便被错误分类，那么就没办法找最优解了，因此样本点被错误分类时要有一定的代价，而正确分类时没有代价。我们将其与 $w^{T} x + b = \pm 1$ 距离作为代价（松弛变量） $ξ \geq 0$ ：

$ξ_{i} = l (y_{i} (w^{T} x_{i} + b) - 1)$

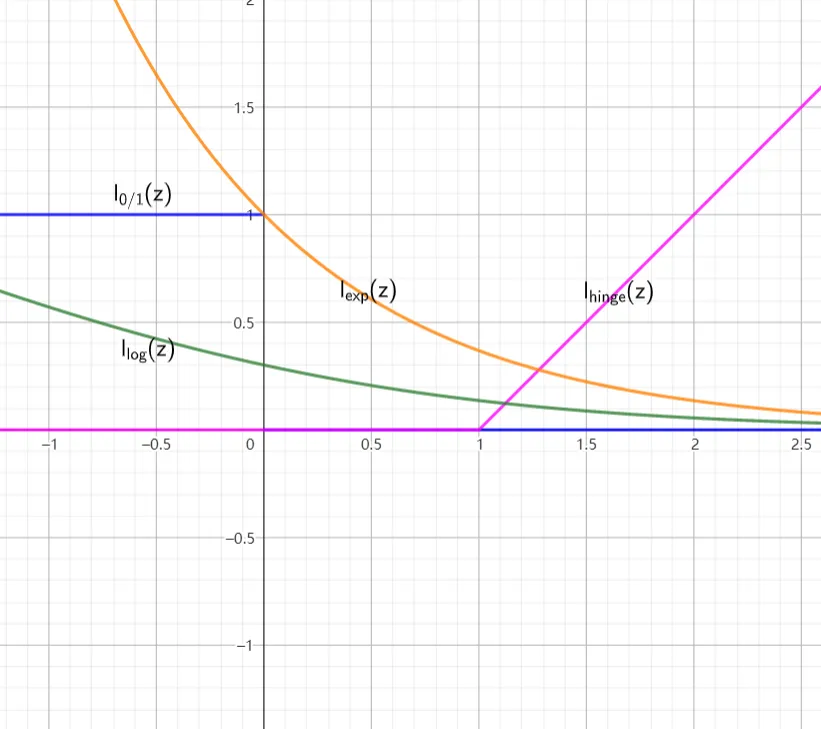
其中， $l (\cdot)$ 可以有多种选择，下面的后三个是连续的函数：

$\begin{aligned} l_{0 / 1} (z) & = {\begin{cases} 1 & z < 0 \\ 0 & otherwise \end{cases} \\ l_{hinge} (z) & = max {0, 1 - z} \\ l_{exp} & = e^{- z} \\ l_{log} & = \log (1 + e^{- z}) \end{aligned}$

它们的函数图像如下：

2.2.2 待求解的问题

将硬间隔 SVM 的问题加上松弛变量后，便是软间隔 SVM 待求解的问题：

$\begin{aligned} min_{w, b} \frac{1}{2} ‖ w ‖^{2} + C \sum_{i = 1}^{m} ξ_{i} \\ s . t . y_{i} (w^{T} x_{i} + b) \geq 1 - ξ_{i} \end{aligned}$

其中 $C$ 的值是松弛量的权重， $C$ 越大即代表优化该问题时，更多考虑松弛量，即让错误分类的样本越少，反之则是允许错误分类的样本越多。

2.2.3 求解支持向量机

软间隔与硬间隔 SVM 的求解过程基本相同，因此下面写的比较简略。

由拉格朗日乘子法，我们列出拉格朗日函数：

$L (w, b, α, ξ, μ) = \frac{1}{2} ‖ w ‖^{2} + C \sum_{i = 1}^{m} ξ_{i} + \sum_{i = 1}^{m} α_{i} (1 - y_{i} (w^{T} x_{i} + b)) - \sum_{i = 1}^{m} μ_{i} ξ_{i}$

由于 $ξ_{i} \geq 0$ ，因此最后一项是减而不是加。

其中 $α_{i} \geq 0, μ_{i} \geq 0$ ，为两种拉格朗日乘子； $m$ 为样本点的数量。

原问题为：

$min_{w, b, ξ} max_{α, μ} L (w, b, α, ξ, μ)$

转化为对偶问题：

$max_{α, μ} min_{w, b, ξ} L (w, b, α, ξ, μ)$

对内层问题，求偏导得到解：

$\begin{aligned} {\begin{cases} \frac{\partial L (w, b, α, ξ, μ)}{\partial w} = w - \sum_{i = 1}^{m} α_{i} y_{i} x_{i} = 0 \\ \frac{\partial L (w, b, α, ξ, μ)}{\partial b} = \sum_{i = 1}^{m} α_{i} y_{i} = 0 \\ \frac{\partial L (w, b, α, ξ, μ)}{\partial ξ_{i}} = C - α_{i} - μ_{i} = 0 \end{cases} \\ \Rightarrow & {\begin{cases} w = \sum_{i = 1}^{m} α_{i} y_{i} x_{i} \\ \sum_{i = 1}^{m} α_{i} y_{i} = 0 \\ C = α_{i} + μ_{i} \end{cases} \end{aligned}$

由 $α_{i} \geq 0, μ_{i} \geq 0, C = α_{i} + μ_{i}$ 可得： $0 \leq α_{i} \leq C$ . 回代后，得到再对外层问题求解：

$\begin{aligned} max_{α} L (α) = max_{α} \sum_{i = 1}^{m} α_{i} - \frac{1}{2} \sum_{i = 1}^{m} \sum_{j = 1}^{m} α_{i} α_{j} y_{i} y_{j} x_{i}^{T} x_{j} \\ \begin{aligned} s . t . & \sum_{i = 1}^{m} α_{i} y_{i} = 0, \\ 0 \leq α_{i} \leq C \\ α_{i} \geq 0 \end{aligned} \end{aligned}$

该问题还需要满足 KKT 条件：

${\begin{cases} α_{i} \geq 0 \\ μ_{i} \geq 0 \\ ξ_{i} \geq 0 \\ μ_{i} ξ_{i} \geq 0 \\ y_{i} (w^{T} x_{i} + b) - 1 + ξ_{i} \geq 0 \\ α_{i} (y_{i} (w^{T} x_{i} + b) - 1 + ξ_{i}) = 0 \end{cases}$

接下来的 SMO 过程一模一样，最后得到：

$α_{2}^{n e w u n c} = α_{2}^{o l d} + \frac{y_{2} (E_{1} - E_{2})}{η}$

然后要对其进行剪辑：

$α_{2}^{n e w} = {\begin{cases} H, & H < α_{2}^{n e w u n c} \\ α_{2}^{n e w u n c}, & L \leq α_{2}^{n e w u n c} \leq H \\ L, & α_{2}^{n e w u n c} < L \end{cases}$

具体的范围如下，对 $y_{1}, y_{2}$ 分类讨论：

$y_{1} = y_{2}$

${\begin{cases} L = max {0, α_{2}^{o l d} - α_{1}^{o l d} - C} \\ H = min {C, α_{2}^{o l d} - α_{1}^{o l d}} \end{cases}$

$y_{1} \neq y_{2}$

${\begin{cases} L = max {0, α_{2}^{o l d} - α_{1}^{o l d}} \\ H = min {C, C + α_{2}^{o l d} - α_{1}^{o l d}} \end{cases}$

3. 非线性 SVM

$φ$ 是一个从低维的输入空间 $X$ 到高维的希尔伯特空间 $H$ 的映射。如果存在函数 $κ (x_{i}, x_{j})$ 对于任意 $x_{i}, x_{j} \in X$ 都有：

$κ (x_{i}, x_{j}) = φ (x_{i}) φ (x_{j})$

就称 $κ (x_{i}, x_{j})$ 为核函数。

通过核函数，我们可以将样本点从低维空间 $X$ 映射到高维 $H$ ，在低维空间中线性不可分的样本点，可能在高维空间中线性可分，由此便可以解决线性不可分的数据。

对于核函数 $κ (x_{i}, x_{j})$ ，我们没有必要知道其对应的 $φ (x)$ 是多少，因为它的表达可能会非常复杂。我们只需要知道 $κ (x_{i}, x_{j})$ 的表达式便可以使用它了。常用的核函数有：

名称	表达式
线性核	$κ (x_{i}, x_{j}) = x_{i}^{T} x_{j}$
多项式核	$κ (x_{i}, x_{j}) = (x_{i}^{T} x_{j})^{d}, d \geq 1$
高斯核	$κ (x_{i}, x_{j}) = \exp (- \frac{‖ x_{i} - x_{j} ‖^{2}}{2 σ^{2}}), σ > 0$
拉普拉斯核	$κ (x_{i}, x_{j}) = \exp (- \frac{‖ x_{i} - x_{j} ‖}{2 σ^{2}}), σ > 0$
Sigmoid 核	$κ (x_{i}, x_{j}) = \tanh (β x_{i}^{T} x_{j} + θ), β > 0, θ < 0$

要使用核函数，公式推导过程和前文一模一样，只需要把公式内的 $x_{i}^{T} x_{j}$ 替换成 $κ (x_{i}, x_{j})$ 就行了。

文章目录

机器学习 | 支持向量机