线性模型 (Linear Model)：给定由 $d$ 个属性描述的示例 $\boldsymbol{x}$，线性模型试图学得一个通过属性间的线性组合来进行预测的函数，即：$f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b$.

1. 线性回归

给定数据集 $D=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),\dots,(\boldsymbol{x}_m,y_m)\}$，其中 $\boldsymbol{x}_i=(x_{i1},x_{i2},\dots,x_{id})^{\mathrm{T}},\;y_i\in\mathbb{R}$. 线性回归试图学得一个线性模型以尽可能准确地预测实值输出标记。

1.1. 单变量线性回归

对于 $d=1$ 的单变量情形，我们的目标是：

$$ \begin{align} (w^*,b^*)&=\underset{(w,b)}{\arg\min}\sum_{i=1}^m(f(x_i)-y_i)^2\\ &=\underset{(w,b)}{\arg\min}\sum_{i=1}^m(y_i-wx_i-b)^2 \end{align} $$

将其分别对 $w,\;b$ 求偏导再置为 $0$，便可得到该问题的解：

$$ \begin{align} &\begin{cases} \displaystyle{\frac{\partial E_{(w,b)}}{\partial w}=2\left(w\sum_{i=1}^mx_i^2-\sum_{i=1}^m(y_i-b)x_i\right)}\\ \displaystyle{\frac{\partial E_{(w,b)}}{\partial b}=2\left(mb-\sum_{i=1}^m(y_i-wx_i)\right)} \end{cases}\\\\ \Rightarrow& \begin{cases} \displaystyle{w=\frac{\sum_{i=1}^m y_i(x_i-\bar{x})}{\sum_{i=1}^mx_i^2-\frac{1}{m}(\sum_{i=1}^mx_i)^2}}\\ \displaystyle{b=\frac{1}{m}\sum_{i=1}^m(y_i-wx_i)} \end{cases} \end{align} $$

上面这个解看着很眼熟，其实就是我们高中就学过的最小二乘法了。

1.2. 多变量线性回归

对于多变量情形，为了式子简便，将 $\boldsymbol{w}$ 和 $b$ 整合到一起得到：

$$ \hat{\boldsymbol{w}}_{(d+1)\times1}= \left( \begin{matrix} \boldsymbol{w}\\ b \end{matrix} \right) $$

对于数据集，最右侧增加一列 $1$：

$$ \mathbf{X}_{m\times(d+1)}= \left( \begin{matrix} x_{11} & x_{12} & \cdots & x_{1d} & 1\\ x_{21} & x_{22} & \cdots & x_{2d} & 1\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ x_{m1} & x_{m2} & \cdots & x_{md} & 1\\ \end{matrix} \right) = \left( \begin{matrix} \boldsymbol{x}_1^{\mathrm{T}} & 1\\ \boldsymbol{x}_2^{\mathrm{T}} & 1\\ \vdots & \vdots\\ \boldsymbol{x}_m^{\mathrm{T}} & 1\\ \end{matrix} \right) $$

标记也写成向量形式：

$$ \boldsymbol{y}_{m\times1}= \left( \begin{matrix} y_1\\ y_2\\ \vdots\\ y_m \end{matrix} \right) $$

综上，我们要求的线性模型便是：

$$ \boldsymbol{y}=\mathbf{X}\hat{\boldsymbol{w}} $$

我们的目标是：

$$ \hat{\boldsymbol{w}}^*=\underset{\hat{\boldsymbol{w}}}{\arg\min}(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{w}}) $$

同样，将其对 $\hat{\boldsymbol{w}}$ 求导得到：

$$ \begin{align} \frac{\partial E_{\hat{\boldsymbol{w}}}}{\partial \hat{\boldsymbol{w}}}&=\frac{\partial }{\partial \hat{\boldsymbol{w}}}(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{w}})\\ &=\frac{\partial }{\partial \hat{\boldsymbol{w}}}(\boldsymbol{y}^{\mathrm{T}}\boldsymbol{y}-\boldsymbol{y}^{\mathrm{T}}\mathbf{X}\hat{\boldsymbol{w}}-\hat{\boldsymbol{w}}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}}\boldsymbol{y}+\hat{\boldsymbol{w}}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}}\mathbf{X}\hat{\boldsymbol{w}})\\ &=-2\mathbf{X}^{\mathrm{T}}\boldsymbol{y}+2\mathbf{X}^{\mathrm{T}}\mathbf{X}\hat{\boldsymbol{w}}\\ &=2\mathbf{X}^{\mathrm{T}}(\mathbf{X}\hat{\boldsymbol{w}}-\boldsymbol{y}) \end{align} $$

在上面推导的第二行到第三行，用到了以下两个结论：

$$ \frac{\partial\boldsymbol{x}^{\mathrm{T}}\mathbf{A}}{\partial\boldsymbol{x}}=\frac{\partial\mathbf{A}^{\mathrm{T}}\boldsymbol{x}}{\partial\boldsymbol{x}}=\mathbf{A}\\ \frac{\partial\boldsymbol{x}^{\mathrm{T}}\mathbf{A}\boldsymbol{x}}{\partial\boldsymbol{x}}=(\mathbf{A}+\mathbf{A}^{\mathrm{T}})\boldsymbol{x} $$

当 $\mathbf{X}^{\mathrm{T}}\mathbf{X}$ 为满秩矩阵或正定矩阵时，将求导得到的式子置为 $0$ 得到：

$$ \hat{\boldsymbol{w}}^*=(\mathbf{X}^{\mathrm{T}}\mathbf{X})^{-1}\mathbf{X}^{\mathrm{T}}\boldsymbol{y} $$

综上，学到的线性模型就是：

$$ f(\hat{\boldsymbol{x}}_i)=\hat{\boldsymbol{x}}_i(\mathbf{X}^{\mathrm{T}}\mathbf{X})^{-1}\mathbf{X}^{\mathrm{T}}\boldsymbol{y} $$

当 $\mathbf{X}^{\mathrm{T}}\mathbf{X}$ 不是满秩矩阵和正定矩阵时，可以解出多个 $\hat{\boldsymbol{w}}$，此时可以引入正则化项来选择最好的解。

1.3 广义线性回归

当样本点的输入和输出不满足线性函数时，上面的线性回归方法就不能直接使用了。不过这个问题的解决办法我们高中也学过，即构造一个单调可微函数 $g(\cdot)$，令：

$$ \begin{align} &g(y)=\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b\\ \Rightarrow\;&y=g^{-1}(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b) \end{align} $$

这样就能解决输入空间到输出空间的非线性函数映射了。

例如若样本点满足 $e^x$ 型的映射，我们可以令 $g(x)=\ln x$，原式就变成：

$$ \begin{align} &\ln y=\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b\\ \Rightarrow\;&y=\exp(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b) \end{align} $$

经过变换后，再套用之前的方法就能解决这个问题了。

2. 对数几率回归（逻辑斯谛回归）

上面的线性回归预测的是实值输出标记，如果我们求的问题是二分类问题的话，就得做一些调整。我们首先要找到一个函数，将一个实数转为 0/1 值，可以用的是单位阶跃函数：

$$ y=\begin{cases} 0,&z<0\\ 0.5,&z=0\\ 1,&z>0 \end{cases} $$

不过这个函数不连续，对后面的计算会有很大的困扰，所以可以换成 Sigmoid 函数：

$$ y=\frac{1}{1+e^{-z}} $$

将其作为 $g^{-1}(\cdot)$ 代入得到：

$$ \begin{align} &y=\frac{1}{1+e^{-(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b)}}\\ \Rightarrow\;&\ln\frac{y}{1-y}=\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b \end{align} $$

将 $y$ 看作 $p(y=1\mid\boldsymbol{x})$，将 $1-y$ 看作 $p(y=0\mid\boldsymbol{x})$，将上式改写为：

$$ \ln\frac{p(y=1\mid\boldsymbol{x})}{p(y=0\mid\boldsymbol{x})}=\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b $$

可以得到：

$$ p(y=1\mid\boldsymbol{x})=\frac{e^{\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b}}{1+e^{\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b}}\\ p(y=0\mid\boldsymbol{x})=\frac{1}{1+e^{\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b}} $$

这个情况不好用求导解决，所以用极大似然估计来估计 $\boldsymbol{w},\;b$，为了式子简洁，首先令：

$$ \boldsymbol{\beta}= \left( \begin{matrix} \boldsymbol{w}\\ b \end{matrix} \right) $$

首先构造似然函数：

$$ \begin{align} &L(\boldsymbol{\beta})=\prod_{i=1}^mp(y_i\mid \boldsymbol{x}_i)\\ \Rightarrow\;&\ln L(\boldsymbol{\beta})=\sum_{i=1}^m\ln p(y_i\mid \boldsymbol{x}_i)\\ \Rightarrow\;&\ln L(\boldsymbol{\beta})=\sum_{i=1}^m\ln(y_ip(y=1\mid\boldsymbol{x})+(1-y_i)p(y=0\mid\boldsymbol{x}))\\ \Rightarrow\;&\ln L(\boldsymbol{\beta})=\sum_{i=1}^m\left(y_i\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i-\ln\left(1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}_i}\right)\right)\\ \end{align} $$

接下来要做的任务便是：

$$ \begin{align} \boldsymbol{\beta}^*&=\underset{\boldsymbol{\beta}}{\arg\max}L(\boldsymbol{\beta})\\ &=\underset{\boldsymbol{\beta}}{\arg\min}-L(\boldsymbol{\beta}) \end{align} $$

可用牛顿法求解：

$$ \boldsymbol{\beta}'=\boldsymbol{\beta}-\left(\frac{\partial^2L(\boldsymbol{\beta})}{\partial\boldsymbol{\beta}\partial\boldsymbol{\beta}^{\mathrm{T}}}\right)^{-1}\frac{\partial L(\boldsymbol{\beta})}{\partial\boldsymbol{\beta}} $$

3. 线性判别分析

线性判别分析的思想是，给定训练样本集，将样本投影到一个直线上，并希望同类样本尽可能近，异类样本尽可能远。得到该直线后，对于新样本，将其投影后根据其投影点的位置判别属于哪一类。图示如下：

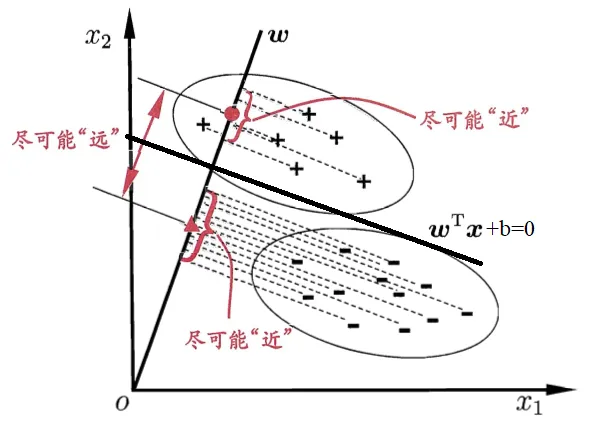
图片来源：《机器学习》周志华

给定数据集 $D=\{(\boldsymbol{x}_i,y_i)\}_{i=1}^m,\;y_i\in\{0,1\}$，令 $i\in\{0,1\}$ 类的集合为 $X_i$，均值向量为 $\boldsymbol{\mu}_i$，协方差矩阵为 $\boldsymbol{\Sigma}_i$.

我们要求一条直线 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b=0$，使其将样本空间分为两部分，这样我们就能够通过样本点在直线的哪一侧来判断类别了。

首先，将样本点投影到直线 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b=0$ 的法向量 $\boldsymbol{w}$，那么它们的均值为 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_i$，协方差为 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\Sigma}_i\boldsymbol{w}$，并且这两个值都是标量。

点 $\boldsymbol{x}$ 投影到向量 $\boldsymbol{w}$ 的投影点的大小为 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}$，下面是简单推导：

设 $\boldsymbol{x}$ 投影到向量 $\boldsymbol{w}$ 的投影点为 $\boldsymbol{p}$，由投影的定义，$\boldsymbol{p}$ 一定与 $\boldsymbol{w}$ 共线，则：$\boldsymbol{p}=c\boldsymbol{w}$

设 $\boldsymbol{p}$ 到 $\boldsymbol{x}$ 的连线为 $\boldsymbol{d}$，由投影的定义，$\boldsymbol{d}\cdot\boldsymbol{p}=0$（或 $\boldsymbol{d}^{\mathrm{T}}\boldsymbol{p}=0$）

$$ \begin{align} &\boldsymbol{d}^{\mathrm{T}}\boldsymbol{p}=0\\ \Rightarrow\;&(\boldsymbol{x}-\boldsymbol{p})^{\mathrm{T}}\boldsymbol{p}=0\\ \Rightarrow\;&(\boldsymbol{x}-c\boldsymbol{w})^{\mathrm{T}}c\boldsymbol{w}=0\\ \Rightarrow\;&\boldsymbol{x}^{\mathrm{T}}c\boldsymbol{w}-c^2\boldsymbol{w}^{\mathrm{T}}\boldsymbol{w}=0\\ \Rightarrow\;&c=\frac{\boldsymbol{x}^{\mathrm{T}}\boldsymbol{w}}{\boldsymbol{w}^{\mathrm{T}}\boldsymbol{w}}=\frac{\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}}{\boldsymbol{w}^{\mathrm{T}}\boldsymbol{w}} \end{align} $$

综上，点 $\boldsymbol{x}$ 投影到向量 $\boldsymbol{w}$ 的投影点为：

$$ \boldsymbol{p}=c\boldsymbol{w}=\frac{\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}}{\boldsymbol{w}^{\mathrm{T}}\boldsymbol{w}}\boldsymbol{w}=\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}\frac{\boldsymbol{w}}{\lVert\boldsymbol{w}\rVert} $$

如果我们只关心大小，不关心方向的话（因为方向一定和 $\boldsymbol{w}$ 一样）：

$$ p=\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x} $$

我们的目标是同类样本尽可能近，异类样本尽可能远，对应到均值方差上就是类别间的均值距离 $\lVert\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_0-\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_1\rVert^2$ 尽可能大，类别内方差 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\Sigma}_0\boldsymbol{w}+\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\Sigma}_1\boldsymbol{w}$ 尽可能小。

$$ \begin{align} J&=\frac{\lVert\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_0-\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_1\rVert^2}{\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\Sigma}_0\boldsymbol{w}+\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\Sigma}_1\boldsymbol{w}}\\ &=\frac{\boldsymbol{w}^{\mathrm{T}}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^{\mathrm{T}}\boldsymbol{w}}{\boldsymbol{w}^{\mathrm{T}}(\boldsymbol{\Sigma}_0+\boldsymbol{\Sigma}_1)\boldsymbol{w}} \end{align} $$

令：

$$ \mathbf{S}_w=\boldsymbol{\Sigma}_0+\boldsymbol{\Sigma}_1\\ \mathbf{S}_b=(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^{\mathrm{T}} $$

则上式可以写为：

$$ J=\frac{\boldsymbol{w}^{\mathrm{T}}\mathbf{S}_b\boldsymbol{w}}{\boldsymbol{w}^{\mathrm{T}}\mathbf{S}_w\boldsymbol{w}} $$

由于 $\boldsymbol{w}$ 为分类边界的法向量，因此我们只关注 $\boldsymbol{w}$ 的方向，而不关注它的长度。因此不妨固定分母 $\boldsymbol{w}^{\mathrm{T}}\mathbf{S}_w\boldsymbol{w}=1$，那么求解 $J$ 最大等价于求解分子最大，也等价于负分子最小，即：

$$ \min_{\boldsymbol{w}}-\boldsymbol{w}^{\mathrm{T}}\mathbf{S}_b\boldsymbol{w}\\ s.t.\;\boldsymbol{w}^{\mathrm{T}}\mathbf{S}_w\boldsymbol{w}=1 $$

用拉格朗日乘子法，构造拉格朗日函数求解：

$$ L(\boldsymbol{w},\lambda)=\boldsymbol{w}^{\mathrm{T}}\mathbf{S}_b\boldsymbol{w}-\lambda(\boldsymbol{w}^{\mathrm{T}}\mathbf{S}_w\boldsymbol{w}-1)\\\\ \begin{align} \frac{\partial L(\boldsymbol{w},\lambda)}{\partial\boldsymbol{w}}&=(\mathbf{S}_b+\mathbf{S}_b^{\mathrm{T}})\boldsymbol{w}-\lambda(\mathbf{S}_w+\mathbf{S}_w^{\mathrm{T}})\boldsymbol{w}\\ &=2(\mathbf{S}_b-\lambda\mathbf{S}_w)\boldsymbol{w}=0 \end{align}\\\\ \begin{aligned} &\Rightarrow \mathbf{S}_b\boldsymbol{w}^*=\lambda\mathbf{S}_w\boldsymbol{w}^*\\ &\Rightarrow \mathbf{S}_w^{-1}\mathbf{S}_b\boldsymbol{w}^*=\lambda\boldsymbol{w}^*\\ &\Rightarrow \mathbf{S}_w^{-1}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^{\mathrm{T}}\boldsymbol{w}^*=\lambda\boldsymbol{w}^*\\ &\Rightarrow \boldsymbol{w}^*=\mathbf{S}_w^{-1}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1) \end{aligned} $$

其中倒数第二行 $(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^{\mathrm{T}}\boldsymbol{w}^*$ 为标量，$\lambda$ 也为标量，由于我们不关心 $\boldsymbol{w}$ 的长度，因此这两个标量我们全部忽略。最后推导成最后一行的结果：$\boldsymbol{w}^*=\mathbf{S}_w^{-1}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)$

上面我们计算出了 $\boldsymbol{w}$，下面还需要计算分类边界的 $b$. 我们可以直接用 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_0$ 和 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_1$ 的平均值，即:

$$ b=\frac{\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_0+\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_1}{2} $$

由于我们的数据集的两种类别数量可能不相同，为了防止先验概率不等造成的干扰，可以对其做加权平均：

$$ b=\frac{m_0\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_0+m_1\boldsymbol{w}^{\mathrm{T}}\boldsymbol{\mu}_1}{m_0+m_1} $$

这样，我们就计算出来了分类边界 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b=0$，要对新数据进行分类时，直接将其代入 $\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b$，如果结果 $>0$，则为分类边界上面的类别，如果结果 $<0$，则为分类边界下面的类别，如果结果 $=0$，则该数据处于分类边界上。