机器学习 | BP 神经网络
人工神经网络 (Artificial Neural Networks, ANN):神经网络是由具有适应性的简单单元组成的广泛并行互联的网络,它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应。
1 神经元模型
人工神经网络的最小单位是神经元,其结构模拟了生物的神经元,具体结构如下:
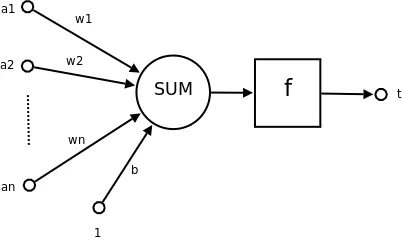
(来源:维基百科,使用 CC BY-SA 3.0 协议)
图中左侧 $a_1,a_2,\dots,a_n$ 代表了上一层神经元的输出,箭头上的数 $w_1,w_2,\dots,w_n$ 代表上一层每一个神经元的连接权重,$b$ 代表偏置,$f(\cdot)$ 代表激活函数,$t$ 代表该神经元的输出。对于上面的符号,它们之间的关系是:
$$ t=f(\sum_{i=1}^nw_ia_i+b) $$
写成向量形式:
$$ t=f(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b) $$
其中激活函数 $f(\cdot)$ 有很多选择,如:
| 函数名 | 表达式 | 取值范围 |
|---|---|---|
| Sigmoid | $f(x)=\frac{1}{1+\exp(-x)}$ | $(0,1)$ |
| ReLU | $f(x)=\max\{0,x\}$ | $[0,\infty)$ |
| tanh | $f(x)=\frac{\exp(x)-\exp(-x)}{\exp(x)+\exp(-x)}$ | $(-1,1)$ |
2 网络结构
ANN 的结构种类有很多种,本轮讨论最经典的结构:多层前馈神经网络。它的结构特点是每层神经元与下一层神经元完全互联,神经元之间不存在同层连接,也不存在跨层连接。它包含三个层次,分别为输入层、隐藏层、输出层,输入层神经元接受外界输入,隐层和输出层神经元对信号进行处理加工,由输出层神经元输出。
一个简单的多层前馈神经网络如下:
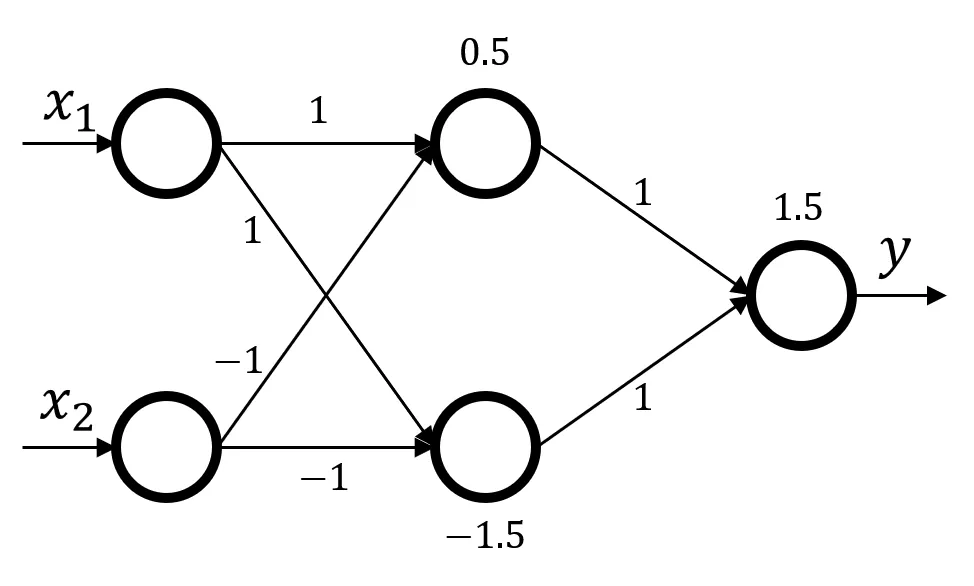
从左到右分别是输入层、隐藏层、输出层,箭头上的数字代表连接权重 $w$,节点上的数字代表偏置 $b$,$x_1,x_2$ 为两个输入的数,$y$ 为输出的数。该网络可以对下面的四个数据进行分类,其中蓝色区域代表 $+$ 类,其他代表 $-$ 类。
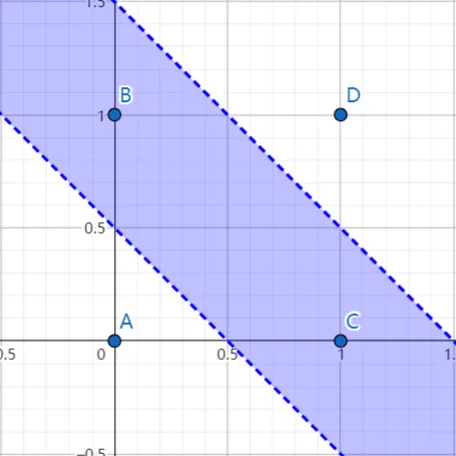
实际情况下,神经网络的结构不会这么简单,它的输入和输出节点数都可能很多,这样它的求解能力更强。例如下面的这个神经网络,接下来的文章将会以它作为例子:
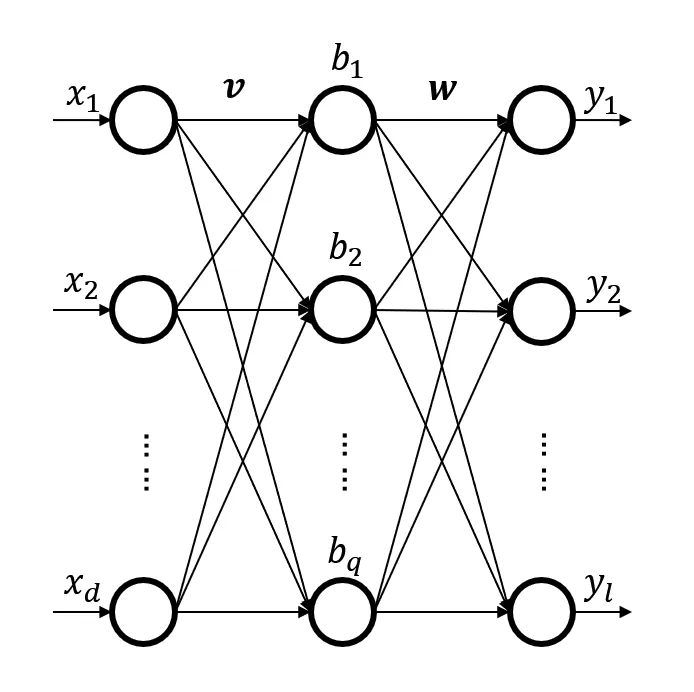
该神经网络输入层有 $d$ 个神经元,隐藏层有 $q$ 个神经元,输出层有 $l$ 个神经元。
- 输入层:输入和输出第 $i$ 个神经元的数据记为 $x_i$.
- 输入层 $\rightarrow$ 隐藏层:输入层第 $i$ 个神经元 $\rightarrow$ 隐藏层第 $j$ 个神经元的连接权值记为 $v_{ij}$.
- 隐藏层:输入第 $j$ 个神经元的值记为 $\displaystyle{\alpha_j=\sum_{i=1}^dv_{ij}x_i}$,偏置为 $\gamma_j$,输出为 $b_j=f(\alpha_j+\gamma_j)$.
- 隐藏层 $\rightarrow$ 输出层:隐藏层第 $j$ 个神经元 $\rightarrow$ 输出层第 $k$ 个神经元的连接权值记为 $w_{jk}$.
- 输出层:输入第 $k$ 个神经元的值记为 $\displaystyle{\beta_k=\sum_{j=1}^qw_{jk}b_j}$,偏置为 $\theta_k$,输出为 $y_k=f(\beta_k+\theta_k)$.
其中,激活函数 $f(\cdot)$ 选择 Sigmoid 函数:$\displaystyle{f(x)=\frac{1}{1+e^{-x}}}$
综上,该神经网络接受的输入为 $\boldsymbol{x}_{d\times 1}$,输出为 $\boldsymbol{y}_{l\times 1}$,网络中包含的参数有:
- $\boldsymbol{v}_{d\times q}$:输入层到隐藏层的权值矩阵
- $\boldsymbol{\gamma}_{q\times1}$:隐藏层的偏置向量
- $\boldsymbol{w}_{q\times l}$:隐藏层到输出层的权值矩阵
- $\boldsymbol{\theta}_{l\times1}$:输出层的偏置向量
参数量为 $dq+q+ql+l$
3 误差逆传播算法
神经网络要学习的实际上就是网络中的参数值,具体来说就是连接权值与偏置。我们需要找到一个合理的方法,通过输入的训练样本数据和样本标记,让神经网络自适应地学习出可以正确分类训练样本。后续就可以使用训练得到的参数,对实际数据进行分类。
误差逆传播 (error BackPropagation, BP) 算法是一个非常有代表的学习算法,利用它进行学习的神经网络叫做 BP 神经网络。
它分为两个阶段:
- 数据流的正向传播:将数据样本输入神经网络,求解出输出。
- 误差信号的反向传播:将输出与样本标签对比,将误差反向传播到每一个节点得到它们需要更新的梯度。
对于每一个训练样例,都会进行上面两个操作(实际的顺序和批次方式可以变化),对于正向传播过程,没有什么难点,就是 $t=f(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b)$ 代进去算出结果来。
该算法核心在于误差的反向传播。首先需要计算误差值,这里使用均方误差 (Mean Squared Error, MSE). 对于第 $p$ 个训练样本 $(\boldsymbol{x}_p,\boldsymbol{y}_p)$,如果神经网络的输出为 $\hat{\boldsymbol{y}}_p=(\hat{y}_1^{(p)},\hat{y}_2^{(p)},\dots,\hat{y}_l^{(p)})$,那么均方误差为:
$$ E_p=\frac{1}{2}\sum_{j=1}^{l}(\hat{y}_j^{(p)}-y_j^{(p)})^2 $$
表达式中的 $1/2$ 只是为了便于求导时消去 $2$,它对误差的相对大小没有影响。
下面我们默认讨论第 $p$ 个训练样本 $(\boldsymbol{x}_p,\boldsymbol{y}_p)$,省略 $p$ 角标。
3.1 更新 $\boldsymbol{w}$
对于 $w_{jk}$ 它的更新是:
$$ w_{jk}\leftarrow w_{jk}+\Delta w_{jk} $$
BP 算法使用梯度下降策略进行更新,给定学习率 $\eta$,具体的更新公式为:
$$ w_{jk}\leftarrow w_{jk}-\eta\frac{\partial E_p}{\partial w_{jk}} $$
对于 $w_{jk}$,可以从网络结构上看到,然后作为求和中的一项影响到 $\beta_k$ 的值,然后作为激活函数的自变量影响到 $\hat{y}_k$ 的值,误差的传递是一个链式的,因此可以用链式求导:
$$ \frac{\partial E_p}{\partial w_{jk}}=\frac{\partial E_p}{\partial \hat{y}_k}\cdot\frac{\partial \hat{y}_k}{\partial \beta_k}\cdot\frac{\partial \beta_k}{\partial w_{jk}} $$
对于第一项:
$$ \begin{align} \frac{\partial E_p}{\partial \hat{y}_k}&=\frac{1}{2}\frac{\partial}{\partial \hat{y}_k}\sum_{j=1}^{l}(\hat{y}_j-y_j)^2\\ &=\frac{1}{2}(2\hat{y}_k-2y_k)\\ &=\hat{y}_k-y_k \end{align} $$
对于第二项:
$$ \frac{\partial \hat{y}_k}{\partial \beta_k}=\hat{y}_k(1-\hat{y}_k) $$
这里能直接转换成这个样子的原因是,对于 Sigmoid 函数 $\displaystyle{f(x)=\frac{1}{1+e^{-x}}}$,它的导数值 $f'(x)=f(x)(1-f(x))$.
对于第三项:
$$ \begin{align} \frac{\partial \beta_k}{\partial w_{jk}}&=\frac{\partial}{\partial w_{jk}}\sum_{i=1}^qw_{ik}b_i\\ &=b_j \end{align} $$
为了简便,我们将第一项与第二项的积记为 $g_k$:
$$ g_k=(\hat{y}_k-y_k)\cdot\hat{y}_k(1-\hat{y}_k) $$
综上:
$$ \Delta w_{jk}=-\eta g_kb_j $$
3.2 更新 $\boldsymbol{\theta}$
对于 $\theta_k$,它的更新是:
$$ \Delta\theta_k=-\eta\frac{\partial E_p}{\partial \theta_k} $$
链式求导:
$$ \frac{\partial E_p}{\partial \theta_k}=\frac{\partial E_p}{\partial \hat{y}_k}\cdot\frac{\partial \hat{y}_k}{\partial \theta_k} $$
对于第二项:
$$ \frac{\partial \hat{y}_k}{\partial \theta_k}=\hat{y}_k(1-\hat{y}_k) $$
综上:
$$ \Delta\theta_k=-\eta g_k $$
3.3 更新 $\boldsymbol{v}$
对于 $v_{ij}$,它的更新是:
$$ \Delta v_{ij}=-\eta\frac{\partial E_p}{\partial v_{ij}} $$
链式求导:
$$ \frac{\partial E_p}{\partial v_{ij}}=\sum_{k=1}^{l}\left(\frac{\partial E_p}{\partial \hat{y}_k}\cdot\frac{\partial \hat{y}_k}{\partial \beta_k}\cdot\frac{\partial \beta_k}{\partial b_j}\right)\cdot\frac{\partial b_j}{\partial \alpha_j}\cdot\frac{\partial\alpha_j}{\partial v_{ij}} $$
这里为什么多出来了个一个求和?原因是输入层 $\rightarrow$ 隐藏层的连接权重会影响到所以输出层节点,所以每个输出层节点的误差都得传递先传递到隐藏层,如下图所示:
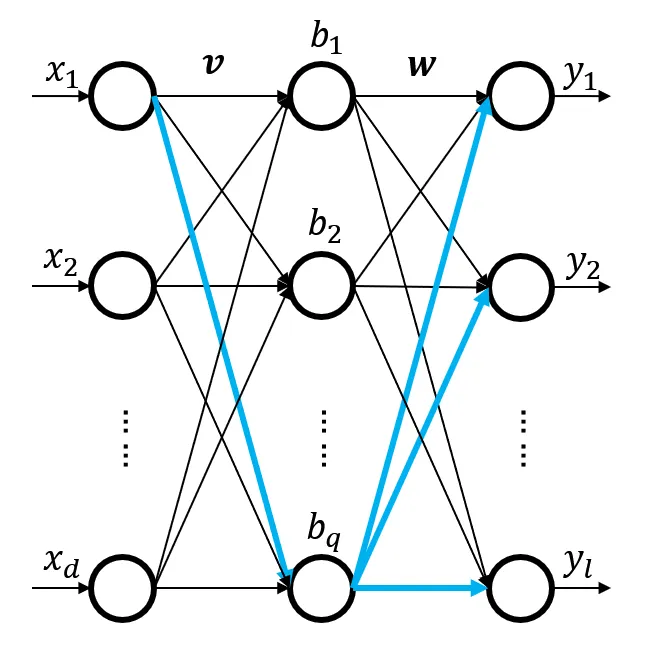
对于求和符号里的第三项:
$$ \begin{align} \frac{\partial \beta_k}{\partial b_j}&=\frac{\partial}{\partial b_j}\sum_{j=1}^qw_{jk}b_j\\ &=w_{jk} \end{align} $$
对于求和符号外面的第一项:
$$ \frac{\partial b_j}{\partial \alpha_j}=b_j(1-b_j) $$
对于求和符号外面的第二项:
$$ \begin{align} \frac{\partial\alpha_j}{\partial v_{ij}}&=\frac{\partial}{\partial v_{ij}}\sum_{i=1}^dv_{ij}x_i\\ &=x_i \end{align} $$
为了简便,我们把求和符号和外面的第一项记为 $e_j$:
$$ \begin{align} e_j&=\sum_{k=1}^{l}\left(\frac{\partial E_p}{\partial \hat{y}_k}\cdot\frac{\partial \hat{y}_k}{\partial \beta_k}\cdot\frac{\partial \beta_k}{\partial b_j}\right)\cdot\frac{\partial b_j}{\partial \alpha_j}\\ &=\sum_{k=1}^{l}\left(g_k\cdot w_{jk}\right)\cdot b_j(1-b_j) \end{align} $$
综上:
$$ \Delta v_{ij}=-\eta e_j x_i $$
3.4 更新 $\boldsymbol{\gamma}$
对于 $\gamma_j$,它的更新是:
$$ \Delta\gamma_j=-\eta\frac{\partial E_p}{\partial \gamma_j} $$
链式求导:
$$ \frac{\partial E_p}{\partial \gamma_j}=\sum_{k=1}^{l}\left(\frac{\partial E_p}{\partial \hat{y}_k}\cdot\frac{\partial \hat{y}_k}{\partial \beta_k}\cdot\frac{\partial \beta_k}{\partial b_j}\right)\cdot\frac{\partial b_j}{\partial \gamma_j} $$
对于求和符号外面的第一项:
$$ \frac{\partial b_j}{\partial \gamma_j}=b_j(1-b_j) $$
综上:
$$ \Delta\gamma_j=-\eta e_j $$
3.5 总结
BP 算法的流程如下:
- 输入:训练集 $D=\left\{(\boldsymbol{x}_p,\boldsymbol{y}_p)\right\}_{p=1}^m$; 学习率 $\eta$.
过程:
- 在 $(0,1)$ 范围随机初始化网络中的所有参数
- repeat
- $\ \ \ \ $for all $(\boldsymbol{x}_p,\boldsymbol{y}_p)\in D$ do
- $\ \ \ \ \ \ \ \ $使用当前参数计算出当前样本输出 $\hat{\boldsymbol{y}}_p$
- $\ \ \ \ \ \ \ \ $计算出 $g_k,e_j$
- $\ \ \ \ \ \ \ \ $计算出 $\Delta w_{jk},\Delta\theta_{k},\Delta v_{ij},\Delta\gamma_{j}$ 并更新参数值
- $\ \ \ \ $end for
- until 达到停止条件
- 输出:参数确定的 BP 神经网络
其中:
$$ \begin{align} &\begin{cases} \displaystyle{g_k=(\hat{y}_k-y_k)\cdot\hat{y}_k(1-\hat{y}_k)}\\ \displaystyle{e_j=\sum_{k=1}^{l}\left(g_k\cdot w_{jk}\right)\cdot b_j(1-b_j)} \end{cases}\\\\ &\begin{cases} \Delta w_{jk}=-\eta g_kb_j\\ \Delta\theta_k=-\eta g_k\\ \Delta v_{ij}=-\eta e_j x_i\\ \Delta\gamma_j=-\eta e_j \end{cases}\\ \end{align} $$
4 代码实现
以下是我使用 C++ 编写的简单神经网络的源代码,可以和上文的公式对照学习:
本文采用 CC BY-SA 4.0 许可,本文 Markdown 源码:Haotian-BiJi