题目 | Bracket Walk

Codeforces Round 877 (Div. 2)

D. Bracket Walk

https://codeforces.com/contest/1838/problem/D

3 seconds / 256 megabytes

standard input / standard output

Problem

There is a string $s$ of length $n$ consisting of the characters '(' and ')'. You are walking on this string. You start by standing on top of the first character of $s$, and you want to make a sequence of moves such that you end on the $n$-th character. In one step, you can move one space to the left (if you are not standing on the first character), or one space to the right (if you are not standing on the last character). You may not stay in the same place, however you may visit any character, including the first and last character, any number of times.

At each point in time, you write down the character you are currently standing on. We say the string is walkable if there exists some sequence of moves that take you from the first character to the last character, such that the string you write down is a regular bracket sequence.

A regular bracket sequence is a bracket sequence that can be transformed into a correct arithmetic expression by inserting characters '1' and '+' between the original characters of the sequence. For example, bracket sequences "()()", "(())" are regular (the resulting expressions are: "(1)+(1)", "((1+1)+1)"), and ")(" and "(" are not.

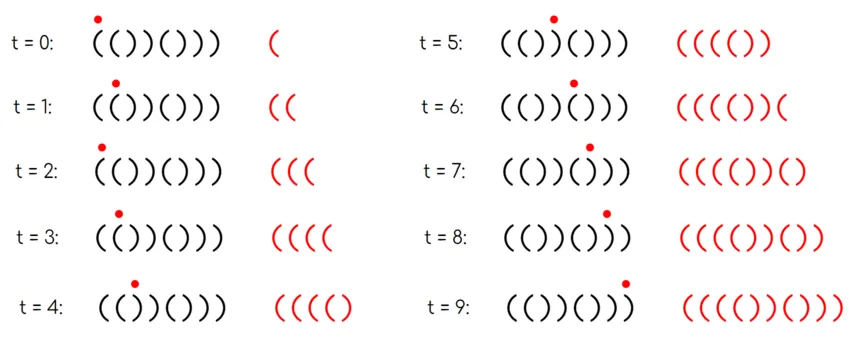
You are given $q$ queries. Each query flips the value of a character from '(' to ')' or vice versa. After each query, determine whether the string is walkable.

Queries are cumulative, so the effects of each query carry on to future queries.

Input

The first line of the input contains two integers $n$ and $q$ ($1\le n,q\le 2\cdot {10}^5$) — the size of the string and the number of queries, respectively.

The second line of the input contains a string $s$ of size $n$, consisting of the characters '(' and ')' — the initial bracket string.

Each of the next $q$ lines contains a single integer $i$ ($1\le i\le n$) — the index of the character to flip for that query.

Output

For each query, print "YES" if the string is walkable after that query, and "NO" otherwise.

You can output the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive responses.

Examples

Input

10 9
(())()()))
9
7
2
6
3
6
7
4
8

Output

YES
NO
NO
YES
NO
YES
NO
NO

Input

3 2
(()
2
3

Output

NO

Note

In the first example:

• After the first query, the string is (())()()(). This string is a regular bracket sequence, so it is walkable by simply moving to the right.
• After the second query, the string is (())()))(). If you move right once, then left once, then walk right until you hit the end of the string, you produce the string (((())()))(), which is a regular bracket sequence.
• After the third query, the string is ()))()))(). We can show that this string is not walkable.

In the second example, the strings after the queries are and , neither of which are walkable.

题解

容易得到，如果括号序列要合法，首先要满足的条件是 $n$ 是偶数，若 $n$ 为奇数直接输出 No，接下来来考虑一般情况。

对于给定的 $n$，我们构造一个“基础序列”，构造方法是正括号与反括号依次填入，例如 $n=6$ 的基础序列：()()().

对于其他序列，我们均可以通过储存它与基础序列的差异来表示，例如 ()(()) 的 $4,5$ 位与基础序列不同，因此可以表示为 $S=\{4,5\}$.

接下来巧妙的点就是如何用这个差异集合来直接得到序列是否满足条件。

首先我们可以通过 $S$ 中元素的奇偶性判断异常类型：

• 如果是奇数，则为 ( 变成了 )，相当于多了一个 )) 序列
• 如果是偶数，则是 ) 变成了 (，相当于多了一个 (( 序列

另外我们可以讨论一下不同序列能否改变序列合法性：

• (): 无论如何都无法改变
• )(: 无论如何都无法改变
• ((: 左右来回走可以向序列中添加 ((
• )): 左右来回走可以向序列中添加 ))

考虑满足条件的情况比较复杂，不如我们来考虑何时不合法：

• $S$ 里的最大值为偶数：偶数代表异常值为 (，最大代表这个 ( 的右侧是 () 序列（或为空）。

  • 例子：()((()

• $S$ 里的最小值为奇数：奇数代表异常值为 )，最小代表这个 ) 的左侧是 () 序列（或为空）。

  • 例子：()))()

由于上面说到，() 无论如何都无法改变序列合法性，那么上面这两种情况一定是不合法的。

---

通过上面两个条件就已经可以解掉这道题目了：

	最大值偶数	最大值奇数
最小值奇数	❌	❌
最小值偶数	❌	✔

不过为了讲的更清楚，我们把剩下的情况也讨论下，看是不是真的是合法的：

$S$ 为空：说明和基础序列一样，肯定合法。

$S$ 里的最大值为奇数，最小值为偶数，序列会是如下结构：

()$\times n$ + (( $\times 1$ + 任意序列 + ))$\times 1$ + ()$\times n$

因此，这个序列有可能不合法的只有中间的任意序列，但是这个任意序列左右被 (( 和 )) 包裹了，因此不管任意序列是怎样的，都可以通过两端的 (( 和 )) 将其转为合法序列。

代码

#include <bits/stdc++.h>
#define endl '\n'

using namespace std;

void solve()
{
    int n, q;
    cin >> n >> q;
    string s;
    cin >> s;
    set<int> st;
    for (int i = 1; i <= n; i++)
        if (i % 2 == 0 && s[i - 1] == '(' ||
            i % 2 == 1 && s[i - 1] == ')')
            st.insert(i);
    while (q--)
    {
        int i;
        cin >> i;
        if (n % 2)
        {
            cout << "No" << endl;
            continue;
        }
        if (st.count(i))
            st.erase(i);
        else
            st.insert(i);
        if (st.size() &&
            (*st.begin() % 2 == 1 ||
             *st.rbegin() % 2 == 0))
            cout << "No" << endl;
        else
            cout << "Yes" << endl;
    }
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    solve();
    return 0;
}