最大期望 (Expectation-maximization, EM) 算法：在统计中被用于寻找，依赖于不可观察的隐性变量的概率模型中，参数的最大似然估计。

1. 问题引入

假如要调查学校中男生与女生分别的身高分布。假设身高分布服从正态分布，那我们要求的参数就是均值 $\mu$ 和方差 $\sigma^2$ . 我们一般的操作是抽取 $100$ 个男生，估计出它们的均值和方差，再抽取 $100$ 个女生，估计出它们的均值和方差。估计的方法可以使用极大似然估计。

但是在有些情况时，我们没办法分别抽 $100$ 个男生和 $100$ 个女生，而是只能抽出 $200$ 个学生，而不知道性别是男是女。此时我们就没有办法直接用极大似然估计分别估计出男生身高分布和女生身高分布的参数了。

我们可以的求解方式是首先随机初始化男生和女生的分布参数，然后根据该分布参数，判断每个数据更可能属于男生还是女生。判断完成后，再使用男生数据和女生数据估计出新的分布参数。重复迭代上面两个步骤，最后参数不再变化或变化很小时，就可以停止算法，输出最后估计出的两个分布的参数了。

这个操作和 EM 算法非常类似。

2. 前置知识

Jensen 不等式

• 若 $f(\cdot)$ 为上凸（下凹）函数，则 $E(f(X))\leq f(E(X))$
• 若 $f(\cdot)$ 为上凹（下凸）函数，则 $E(f(X))\geq f(E(X))$

这个不等式的两点形式是我们非常熟悉的结论，例如下凸（我们下面的推导均用下凸函数，另一种类比推理即可）二次函数 $f(x)=x^2$ 取两点 $x_1,x_2$，那么 $\frac{f(x_1)+f(x_2)}{2}\geq f(\frac{x_1+x_2}{2})$.

这个用形式化的表述便是：

$$ af(x_1)+(1-a)f(x_2)\geq f(ax_1+(1-a)x_2) $$

Jensen 不等式不局限于两点，而是可以推广到任意点集：

$$ \sum_{i=1}^{n}\lambda_if(x_i)\geq f(\sum_{i=1}^{n}\lambda_ix_i) $$

下面做 Jensen 不等式的数学归纳法推导：

对于任意点集 $x_1,x_2,\dots,x_n$ 与它对应的参数 $\lambda_1,\lambda_2,\dots,\lambda_n$，其中 $\lambda_i\geq0$ 且 $\sum_{i=1}^{n}\lambda_i=1$，那么：

$i=1,2$ 时，易得 Jensen 不等式 $\sum_{i=1}^{n}\lambda_if(x_i)\geq f(\sum_{i=1}^{n}\lambda_ix_i)$ 成立。

接下来我们假设 $i=M$ 时，Jensen 不等式 $\sum_{i=1}^{n}\lambda_if(x_i)\geq f(\sum_{i=1}^{n}\lambda_ix_i)$ 成立。

那么当 $i=M+1$ 时，

$$ \begin{align} &f\left(\sum_{i=1}^{M+1}\lambda_ix_i\right)\\ =&f\left(\sum_{i=1}^{M}\lambda_ix_i+\lambda_{M+1}x_{M+1}\right)\\ =&f\left((1-\lambda_{M+1})\sum_{i=1}^{M}\frac{\lambda_i}{1-\lambda_{M+1}}x_i+\lambda_{M+1}x_{M+1}\right)\\ &\text{用 }i=2\text{ 时的 Jensen 不等式进行转换:}\\ \leq&(1-\lambda_{M+1})f\left(\sum_{i=1}^{M}\frac{\lambda_i}{1-\lambda_{M+1}}x_i\right)+f(\lambda_{M+1}x_{M+1})\\ \end{align} $$

由于 $\sum_{i=1}^{M+1}\lambda_i=1$，那么：

$$ \sum_{i=1}^{M}\lambda_i=1-\lambda_{M+1}\\ \sum_{i=1}^{M}\frac{\lambda_i}{1-\lambda_{M+1}}=1 $$

那么：

$$ \begin{align} &(1-\lambda_{M+1})f\left(\sum_{i=1}^{M}\frac{\lambda_i}{1-\lambda_{M+1}}x_i\right)+f(\lambda_{M+1}x_{M+1})\\ =&(1-\lambda_{M+1})\left(\sum_{i=1}^{M}\frac{\lambda_i}{1-\lambda_{M+1}}f(x_i)\right)+f(\lambda_{M+1}x_{M+1})\\ =&\sum_{i=1}^{M}\lambda_if(x_i)+f(\lambda_{M+1}x_{M+1})\\ =&\sum_{i=1}^{M+1}\lambda_if(x_i) \end{align} $$

综上，若假设 $i=M$ 时，Jensen 不等式成立，我们可以推出 $i=M+1$ 时，Jensen 不等式也成立。

又因为 $i=1,2$ 时，Jensen 不等式成立，因此我们可以推广到 $i$ 等于任何正整数的情况，证毕。

3. 算法推导

3.1 问题表示

对于知道样本属于的分布的情况，记分布参数为 $\theta$，我们使用极大似然估计的时候的流程首先是构造似然函数：

$$ \begin{align} L(\theta)&=\prod_{i=1}^{n}p(x_i\mid\theta)\\ \Rightarrow\;\ln L(\theta)&=\sum_{i=1}^{n}\ln p(x_i\mid\theta) \end{align} $$

然后得到了对数似然函数后，我们将其最大化即可得到估计的分布参数 $\theta^*$：

$$ \theta^*=\underset{\theta}{\arg\max}\sum_{i=1}^{n}\ln p(x_i\mid\theta) $$

接下来我们往往就是对它求偏导再置零，把参数这样算出来。

但是我们这个问题中，样本有未观察到的隐含数据 $\boldsymbol{z}=(z_1,z_2,\dots,z_n)$，比如我们不确定样本属于哪个分布，那么我们得引入隐变量：

$$ p(x_i\mid\theta)=\sum_{z_i}p(x_i,z_i\mid\theta) $$

将其代入似然函数，则似然函数为：

$$ \begin{align} L(\theta)&=\prod_{i=1}^{n}\sum_{z_i}p(x_i,z_i\mid\theta)\\ \Rightarrow\;\ln L(\theta)&=\sum_{i=1}^{n}\ln\sum_{z_i}p(x_i,z_i\mid\theta) \end{align} $$

然后我们就要将对数似然函数最大化，得到估计的分布参数 $\theta^*$：

$$ \theta^*=\underset{\theta}{\arg\max}\sum_{i=1}^{n}\ln\sum_{z_i}p(x_i,z_i\mid\theta) $$

但是目前的情况，$\ln(\cdot)$ 里面含有很多元素的累加，对它求偏导置为零是极为复杂的，没有办法直接用求偏导极大似然把 $\theta^*$ 给估计出来，因此得使用一些特殊技巧。

3.2 问题求解

3.2.1 Expectation 步骤

对于对数似然函数，我们进行如下变换：

$$ \ln L(\theta)=\sum_{i=1}^{n}\ln\sum_{z_i}p(x_i,z_i\mid\theta)=\sum_{i=1}^{n}\ln\sum_{z_i}Q_i(z_i)\frac{p(x_i,z_i\mid\theta)}{Q_i(z_i)} $$

即在分子分母同乘一个 $Q_i(z_i)$，这个分布是我们引入的一个未知的新的分布，用于辅助求解问题。

我们现在关注到内层求和的式子：

$$ \sum_{z_i}Q_i(z_i)\frac{p(x_i,z_i\mid\theta)}{Q_i(z_i)} $$

我们可以将其看成随机变量 $\frac{p(x_i,z_i\mid\theta)}{Q_i(z_i)}$ 的期望 $E(x)$.

$X$ 的期望的表达式如下：

$$ E(X) = \sum_{i=1}^n{p(x_i)x_i} $$

对照着期望的表达式，我们的转换方式是将式子中的 $Q_i(z_i)$ 看作 $p(x_i)$， $\frac{p(x_i,z_i\mid\theta)}{Q_i(z_i)}$ 看作 $x_i$

我们知道 $\ln(\cdot)$ 为下凹函数，由 Jensen 不等式可知：

$$ \ln E(X)\geq E(\ln X) $$

对我我们这个式子，即：

$$ \begin{align} \ln L(\theta)=\sum_{i=1}^{n}\ln\sum_{z_i}p(x_i,z_i\mid\theta)=&\ \sum_{i=1}^{n}\ln\sum_{z_i}Q_i(z_i)\frac{p(x_i,z_i\mid\theta)}{Q_i(z_i)}\\ \geq&\sum_{i=1}^{n}\sum_{z_i}Q_i(z_i)\ln\frac{p(x_i,z_i\mid\theta)}{Q_i(z_i)} \end{align} $$

这个操作相当于我们把求和提到 $\ln(\cdot)$ 的外面了，这样就不会存在 $\ln(\cdot)$ 里面含有很多元素的累加这种复杂情况了。

通过这个操作得到了原对数似然函数 $\ln L(\theta)$ 的下界，如果我们能够将这个下界逐渐变大，当不等式取等号的时候，就取到了最大的下界，我们要找的就是取等号情况的 $Q_i(z_i)$.

这个地方求的最大的下界是什么意思非常重要，要注意我们要求的是最大的下界，注意与下界的最大做区分。

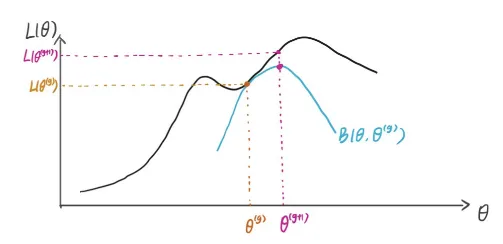
我们用下图作解释（图片来源：知乎专栏）

假设我们此时的参数为 $\theta^{(g)}$，我们可以得到的是 $\ln L(\theta)$ 的一个下界 $B(\theta,\theta^{(g)})$，我们的任务就是找到最大的下界，即找到在 $\theta^{(g)}$ 时与 $\ln L(\theta)$ 相等的下界。这个下界是最大的，因为再大的话就不满足不等式条件了。

若要满足 Jensen 不等式等号成立，要满足：

$$ \frac{p(x_i,z_i\mid\theta)}{Q_i(z_i)}=\text{常数 }C $$

由于我们引入的 $Q_i(z_i)$ 是一个分布，满足 $\sum_{z}Q_i(z_i)=1$，那么：

$$ \begin{align} &p(x_i,z_i\mid\theta)=CQ_i(z_i)\\ \Rightarrow&\sum_z p(x_i,z_i\mid\theta)=C\sum_z Q_i(z_i)\\ \Rightarrow&\sum_z p(x_i,z_i\mid\theta)=C \end{align} $$

将算出来的 $C$ 的表达式回代到之前的式子：

$$ \frac{p(x_i,z_i\mid\theta)}{Q_i(z_i)}=\sum_z p(x_i,z_i\mid\theta)\\ \Rightarrow Q_i(z_i)=\frac{p(x_i,z_i\mid\theta)}{\sum_z p(x_i,z_i\mid\theta)}=\frac{p(x_i,z_i\mid\theta)}{p(x_i\mid\theta)}=p(z_i\mid x_i,\theta) $$

这样我们就把 $Q_i(z_i)$ 分布表示出来了，那么 $\ln L(\theta)$ 的最大下界就是：

$$ \sum_{z_i}p(z_i\mid x_i,\theta)\ln\frac{p(x_i,z_i\mid\theta)}{p(z_i\mid x_i,\theta)} $$

至此，EM 算法的 E 步就完成了，即我们找到了让最大下界的 $Q_i(z_i)$ 的表达式。

3.2.2 Maximization 步骤

接下来的任务就是找到下界的最大值了：

$$ \theta^*=\underset{\theta}{\arg\max}\sum_{i=1}^{n}\sum_{z_i}Q_i(z_i)\ln\frac{p(x_i,z_i\mid\theta)}{Q_i(z_i)} $$

这个便是 EM 算法的 M 步，把这个下界的最大值时的 $\theta^*$ 求出来，再重新回到 E 步，迭代运行，就能慢慢得收敛到最大值。

还是用刚才那张图做解释：

E 步我们找到的是最大的下界，M 步我们就是找下界的最大值，即找到 $B(\theta,\theta^{(g)})$ 最大时的 $\theta^{(g+1)}$。

找到之后，我们再在 $\theta^{(g+1)}$ 点找到最大的下界 $B(\theta,\theta^{(g+1)})$，再找到 $B(\theta,\theta^{(g+1)})$ 最大时的 $\theta^{(g+2)}$，如此循环迭代，最后就能迭代得到最大的 $\theta$.

4 总结

EM 算法的总体思路大概就是 $\ln L(\theta)$ 不好直接极大化求出来 $\theta^*$，因此用 Jensen 不等式这个方法，用随机初始化的 $\theta^(t)$ 求出来一个 $\ln L(\theta)$ 的下界。首先要找到最大的这个下界，然后再对这个下界做极大化找到新一轮的 $\theta^{(t+1)}$，然后再在 $\theta^{(t+1)}$ 的基础上找到最大的下界，再极大化找到 $\theta^{(t+2)}$...... 如此到最后收敛的时候，就能找到最终的 $\theta^*$ 了。

这个过程如下图所示：

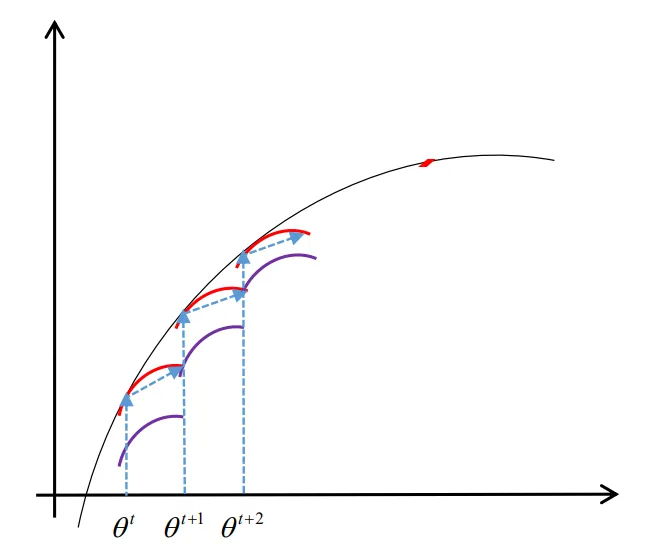
算法步骤便是：

1. 随机初始化初始参数 $\theta_0$

2. 开始 EM 算法迭代：

   • E 步

     • 计算得到 $Q_i(z_i)=p(z_i\mid x_i,\theta^{(j)})$
     • 计算得到 $l(\theta,\theta^{(j)})=\sum_{i=1}^{n}\sum_{z_i}Q_i(z_i)\ln\frac{p(x_i,z_i\mid\theta^{(j)})}{Q_i(z_i)}$

   • M 步

     • 计算得到 $\theta^{(j+1)}=\underset{\theta}{\arg\max}\ l(\theta,\theta^{(j)})$

   • 判断

     • 如果收敛，则跳出循环结束算法，否则用 $\theta^{(j+1)}$ 进行新的一次迭代
3. 输出求到的参数 $\theta$