“范式杯”2023牛客暑期多校训练营1

H - Matches

https://ac.nowcoder.com/acm/contest/57355/H

题意

给定两个长度为 $n$ 的序列 $\{a\}_{i=1}^n$ 和 $\{b\}_{i=1}^n$, 现在可以选择其中一个序列交换其中的两个数字, 问经过至多一 次操作后最小的 $\sum_{i=1}^n\left|a_i-b_i\right|$。$1 \leq n \leq 2 \times 10^5, 0 \leq\left|a_i\right|,\left|b_i\right| \leq 10^{12}$ 。

题解

对于一对 $(a_i,b_i),(a_j,b_j)$，如果它们的大小关系相同，称为正序，若相反成为反序。另外，如果其中区间将另一个区间包含起来，称为包络，如果一个区间和另一个区间有交集，则称为相交。

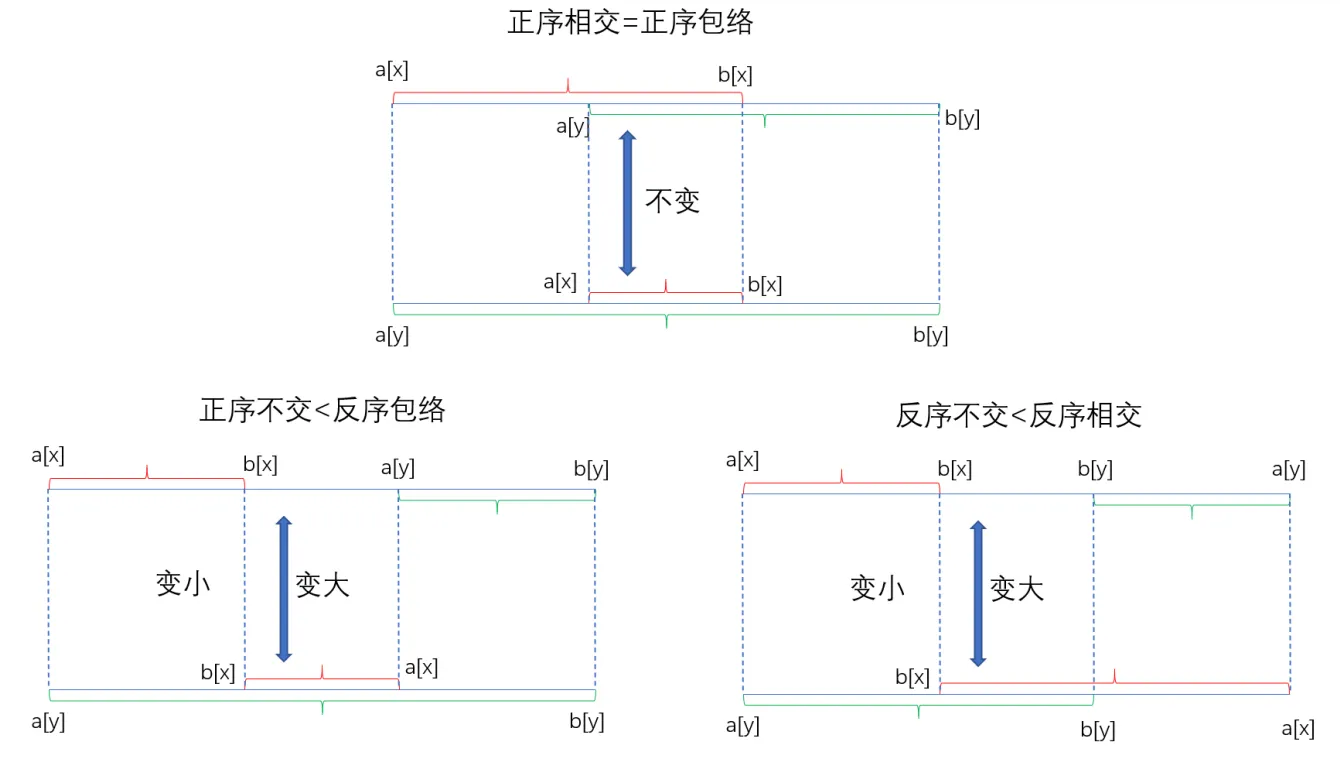
如上图，对于一对 $(a_i,b_i),(a_j,b_j)$，交换后差值减小的情况只有反序包络与反序相交。因此考虑交换时，只需要考虑这两种情况。另外，差值减小的幅度 $\Delta$ 和两个区间相交的长度有关，具体来说，若两个反序区间相交的距离为 $\text{cross}$，那么 $\Delta=2\cdot\text{cross}$. 因此，在选择包络或相交的区间时，要选择相交长度最长的。

首先，我们将区间分成两类，$a<b$ 的区间的集合为 $s$，$a>b$ 的区间的集合为 $t$，另外 $a=b$ 的情况不会对最终答案产生影响，所以直接忽略。那我们的思路就变成，遍历其中一个集合的每一个区间，在另一个集合中找与其包络或相交的区间，下面代码遍历的 $t$.

那现在的问题就是，对于 $t$ 中每一个区间，如何快速的在 $s$ 中找到符合要求的最好的区间。

首先容易发现，如果 $s$ 中一个区间被另一个区间完全包含，那么我们选择大的区间，答案一定不会比小区间差。因为上文说到相交长度越长，减小幅度越大，$s$ 中大区间与当前 $t$ 中的区间的相交长度一定 $\geq$ $s$ 中被包含的小区间的相交长度。因此，应当将 $s$ 中的所有有包含关系的区间去除，保留最大区间。

经过上面的操作后，只要在 $s$ 中选择一个符合条件的区间，则必为对应条件的最优区间。由于 $s$ 中没有互相包含的区间，因此获得一个新性质，我们对 $s$ 的左端点进行排序后，$s$ 的右端点其实也有序了，这样的话左右端点都可以用二分找到了。

对于 $t$ 中的一个区间 $(x,y)$：

  • 找 $s$ 中与它相交的

    • 找左侧相交的：在 $s$ 中区间二分找左端点 $\leq x$ 的
    • 找右侧相交的：在 $s$ 中区间二分找右端点 $\geq y$ 的

  • 找 $s$ 中与它包络的

    • 在 $s$ 中区间二分找左端点 $\leq x$ 的索引 $l$，找右端点 $\geq y$ 的索引 $r$，那么 $(l,r)$ 的区间就是被 $t$ 包络。

代码

#include <bits/stdc++.h>
#define endl '\n'
#define int long long

using namespace std;

void solve()
{
    int n;
    cin >> n;
    vector<pair<int, int>> a(n);
    int sum = 0, cross = 0;
    for (auto &p : a)
        cin >> p.first;
    for (auto &p : a)
        cin >> p.second;
    vector<pair<int, int>> s, t;
    for (auto &[x, y] : a)
    {
        sum += abs(x - y);
        if (x < y)
            s.emplace_back(x, y);
        else if (x > y)
            t.emplace_back(y, x);
    }
    sort(s.begin(), s.end());
    vector<int> sx, sy, len;
    int rpos = INT64_MIN;
    for (auto &[x, y] : s)
    {
        if (y <= rpos)
            continue;
        rpos = y;
        sx.push_back(x);
        sy.push_back(y);
        len.push_back(y - x);
    }
    for (auto &[x, y] : t)
    {
        int tmp = 0;
        int lpos = upper_bound(sx.begin(), sx.end(), x) - sx.begin();
        int rpos = lower_bound(sy.begin(), sy.end(), y) - sy.begin();
        if (lpos > 0)
            tmp = max(tmp, min(y - x, sy[lpos - 1] - x));
        if (rpos < sy.size())
            tmp = max(tmp, min(y - x, y - sx[rpos]));
        if (rpos > lpos)
            tmp = max(tmp, *max_element(len.begin() + lpos, len.begin() + rpos));
        cross = max(cross, tmp);
    }
    cout << sum - cross * 2 << endl;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    solve();
    return 0;
}