ST 表 (Sparse Table)：对于可重复贡献问题，可在 $O(n\log n)$ 完成初始化，在 $O(1)$ 回答每个区间查询的数据结构。但是不支持修改数据。

可重复贡献问题：对于运算 $\star$，如果 $x\star x=x$，且 $\star$ 要满足结合律，则对应的区间询问是可重复贡献问题。符合这个性质的常见运算有 $\max,\min,\gcd$.

ST 表

预处理

对于一个数列，ST 表储存的便是其二的幂次长度的每一段的计算结果。

具体点来说，如果一个数列长度为 $9$，我们用中括号 $[l,r]$ 表示要查询的区间，那么 ST 表储存的便是：

• 长度为 $1$ 的结果：$[1,1],[2,2],[3,3],[4,4],[5,5],[6,6],[7,7],[8,8],[9,9]$
• 长度为 $2$ 的结果：$[1,2],[2,3],[3,4],[4,5],[5,6],[6,7],[7,8],[8,9]$
• 长度为 $4$ 的结果：$[1,4],[2,5],[3,6],[4,7],[5,8],[6,9]$
• 长度为 $8$ 的结果：$[1,8],[2,9]$

将区间可视化的话如下图：

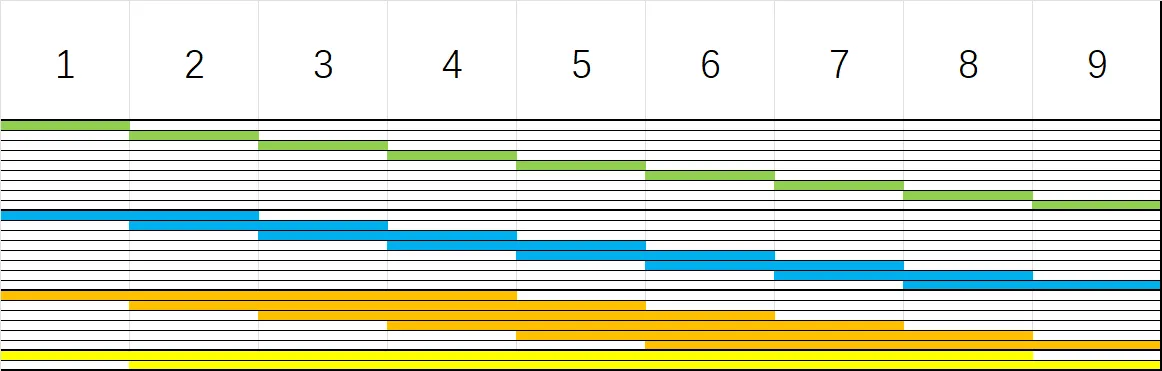
对于长度为 $n$ 的数列，将要计算 $\log n$ 个不同长度的结果，每种长度结果的数量级为 $n$. 那么预处理的时间复杂度为：$O(n\log n)$

预处理数据储存在一个二维数组 $f$ 内，第一维为区间长度，第二维为区间起始下标：

• 首先读入数列，储存到长度为 $1$ 的结果内
• 然后通过上一层的结果递推本层结果。即：对于 $2^k$ 长度的结果，使用 $2^{k-1}$ 的结果进行计算。转移方程为（$\star$ 代表具体场景的运算）：$f_{i,j}=\star(f_{i-1,j},f_{i-1,j+2^{i-1}})$

求解

由于 ST 表解决的是可重复贡献问题，那么两个有重复部分的区间的进行计算的话，并不会影响答案的正确性。

具体点来说，如果我们要求一个数列的区间 $[2,8]$ 的最大值，那么我们对 $[2,6]$ 的最大值和 $[4,8]$ 的最大值取最大值，就能得到 $[2,8]$ 的最大值。

对于任意一个区间 $[l,r]$，我们都可以分解为上面预处理出来的两个区间，具体分解方式如下：

• 记区间长度为 $d=r-l+1$
• 分解出来的两个区间的长度为 $d'=2^{\lfloor\log_2 d\rfloor}$ （相当于找到 $\leq d$ 的最大的 $2$ 的幂次）
• 分解出来的区间为：$[l,l+(d'-1)]$ 和 $[r-(d'-1),r]$

将区间分解好后，我们就用上面预处理得到的结果直接计算出答案。

因此可以在 $O(1)$ 取得任意一个区间的结果。

模板

运算为 $\max$，数列长度为 $N$.

预处理

void init()
{
    for (int i = 1; i <= N; i++)
        cin >> f[0][i];
    for (int i = 1; i <= LOGN; i++)
        for (int j = 1; j <= N - (1 << i) + 1; j++)
            f[i][j] = max(f[i - 1][j], f[i - 1][j + (1 << (i - 1))]);
}

查询

int query(int l, int r)
{
    int len = r - l + 1;
    int pow = 0, pow2 = 1;
    while (pow2 * 2 <= len)
    {
        pow++;
        pow2 *= 2;
    }
    return max(f[pow][l], f[pow][r - pow2 + 1]);
}

此处每次查询都计算了一遍 $2$ 的幂次，实际可以先预处理计算出来，不需要每次都算一遍。