数据结构 | 线段树
线段树 (Segment Tree):用来维护区间信息的数据结构。可在 $O(\log N)$ 的时间复杂度内完成单点修改、区间修改、区间查询(区间和、区间最大值、区间最小值)等操作。
1 线段树
建议看线段树之前先看树状数组,因为线段树相当于加强了树状数组的功能,先看树状数组便于理解线段树。
我们首先简单复习下树状数组,对于一个长度为 $9$ 的数列 $1,2,\dots,9$,树状数组储存了 $9$ 个数,这 $9$ 个数分别为原数组不同区间的和,它们的分布如下:(图中 Array 为原数组,BIT 为树状数组)
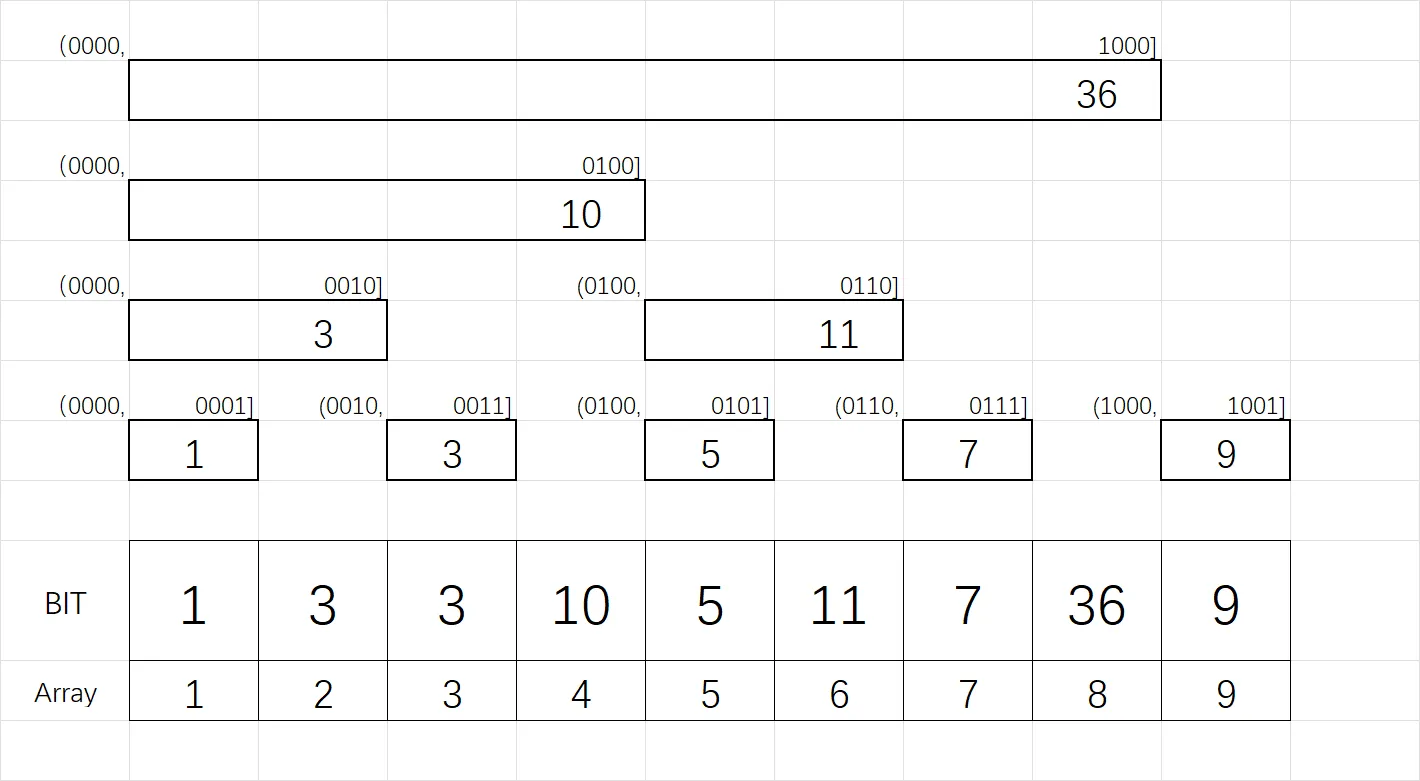
可以发现,树状数组储存的区间不存在加起来覆盖范围重复的,即任意挑选一个区间,无法分成两个已有的区间。
1.1 建树
线段树和树状数组思路类似,也是储存数列不同区间的和,对于一个长度为 $9$ 的数列 $1,2,\dots,9$,线段树储存了 $17$ 个数分别为原数组不同区间的和,它们的分布如下:(图中 Array 为原数组,Segment Tree 为线段树)
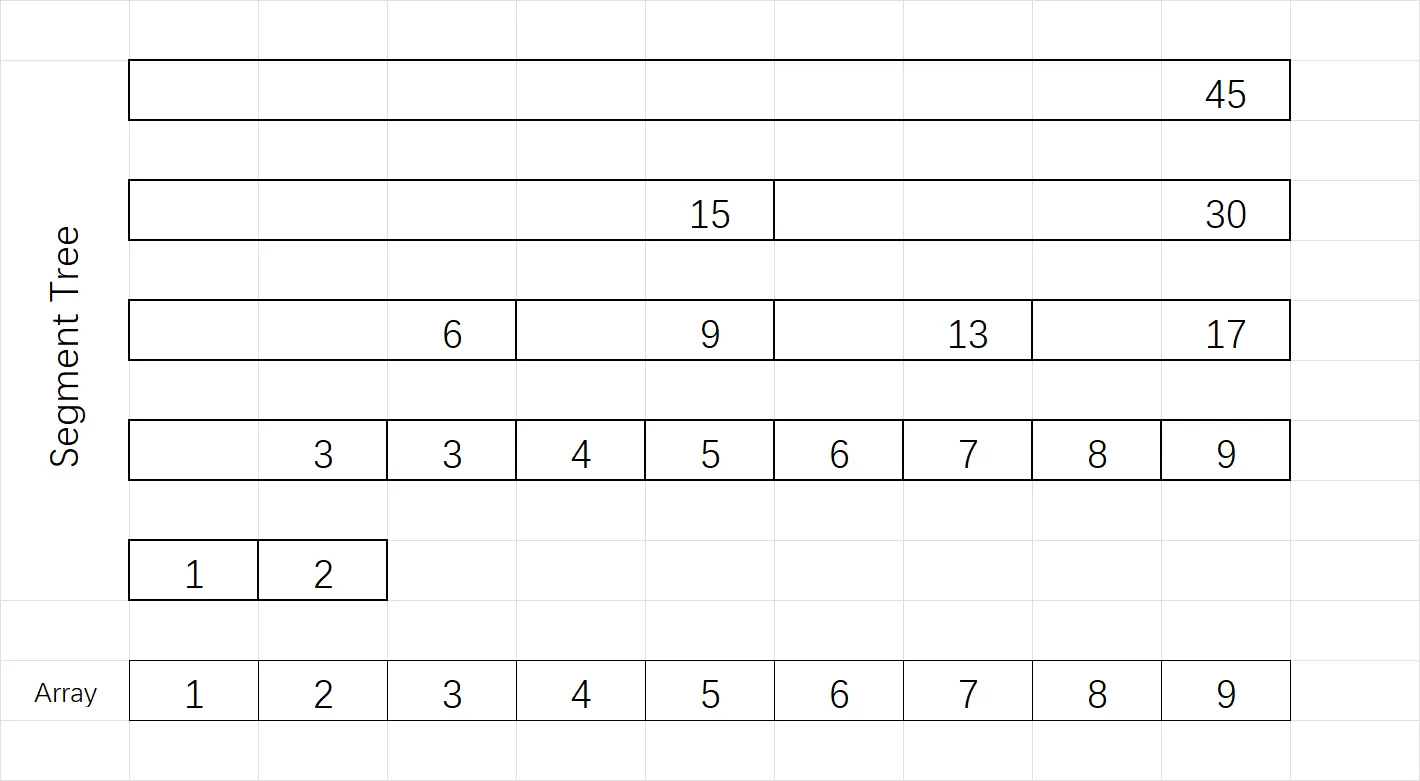
可以发现线段树储存的区间更多,有很多区间加起来的覆盖范围是已有的区间,或者换一种说法,每个区间都是从最大的区间二分分解出来的。
实际上,所有区间组成了一颗完全二叉树,左右节点的和等于父节点。根节点下标 $1$,若父节点下标 $x$,则左子节点下标 $2x$,右子节点下标 $2x+1$. 若父节点的范围为 $[s,t]$,则左子节点的范围为 $[s,\lfloor\frac{s+t}{2}\rfloor]$,右子节点的范围为 $[\lfloor\frac{(s+t)}{2}\rfloor+1,t]$.
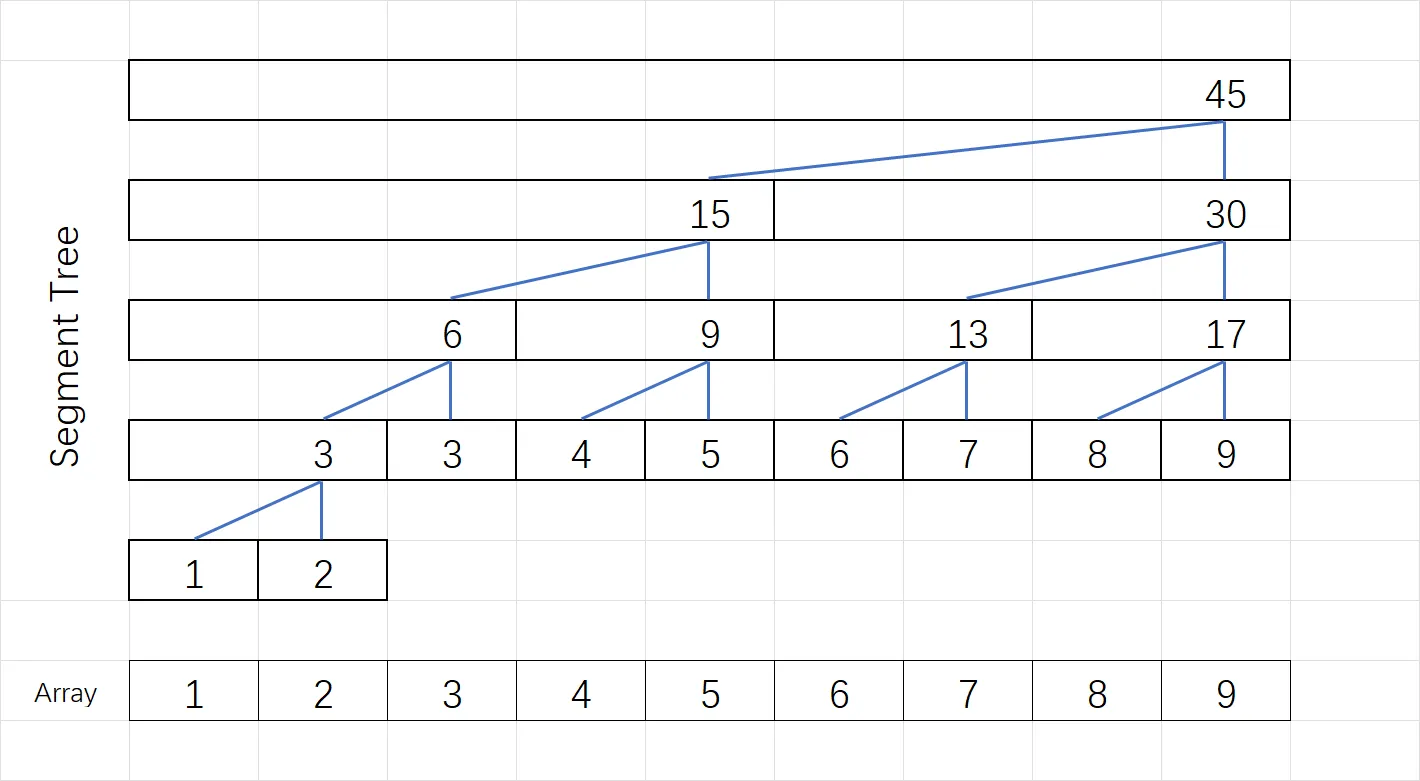
根据上述结构,用递归可以很方便地构建线段树,代码如下:
void build(int s, int t, int p)
{
if (s == t)
{
sum[p] = a[s];
return;
}
int m = (s + t) / 2;
build(s, m, p * 2);
build(m + 1, t, p * 2 + 1);
sum[p] = sum[p * 2] + sum[p * 2 + 1];
}函数参数解释,下面的所有代码保持一致,后文不再重复解释:
$[l, r]$:指定的需要进行操作的区间
$c$:指定操作的目标值(例如增加量、修改的结果)
$[s, t]$:当前递归函数正在处理的节点对应的区间,初始调用时指定为 $[1,n]$
$p$:当前递归函数正在递归处理的节点编号,初始调用时指定为 $1$
1.2 区间查询
线段树进行区间查询时的思路就是,将要查询的区间 $[l,r]$ 分解为线段树内储存的区间。分解逻辑如下:
由长分解到短,对于长度为 $n$ 的数列,初始时考察区间为全体:$s=1,t=n$.
- 如果线段树内的区间 $[s,t]$ 完全被 $[l,r]$ 包含,则它的值加入结果。
否则,则考察它的左右子区间,令分界点 $m=\lfloor\frac{s+t}{2}\rfloor$:
如果 $[s,t]$ 的左子区间 $[s,m]$ 与 $[l,r]$ 有交集($l\leq m$)
- 递归考察 $[s,m]$ 区间
如果 $[s,t]$ 的右子区间 $[m+1,t]$ 与 $[l,r]$ 有交集($m+1\leq r$)
- 递归考察 $[m+1,t]$ 区间
- 如果上面的情况都不满足,则说明 $[s,t]$ 区间与我们要求的 $[l,r]$ 区间完全不相交,直接跳过。
下图为一个示例,下图数组 $1,2,\dots,8,9$,黄色为要求和的区间 $[3,8]$,蓝色和绿色为考察过的区间,其中绿色为被完全包含的区间,它的值被加入结果。所以区间和结果为 $((3+9)+(13+8))=33$.
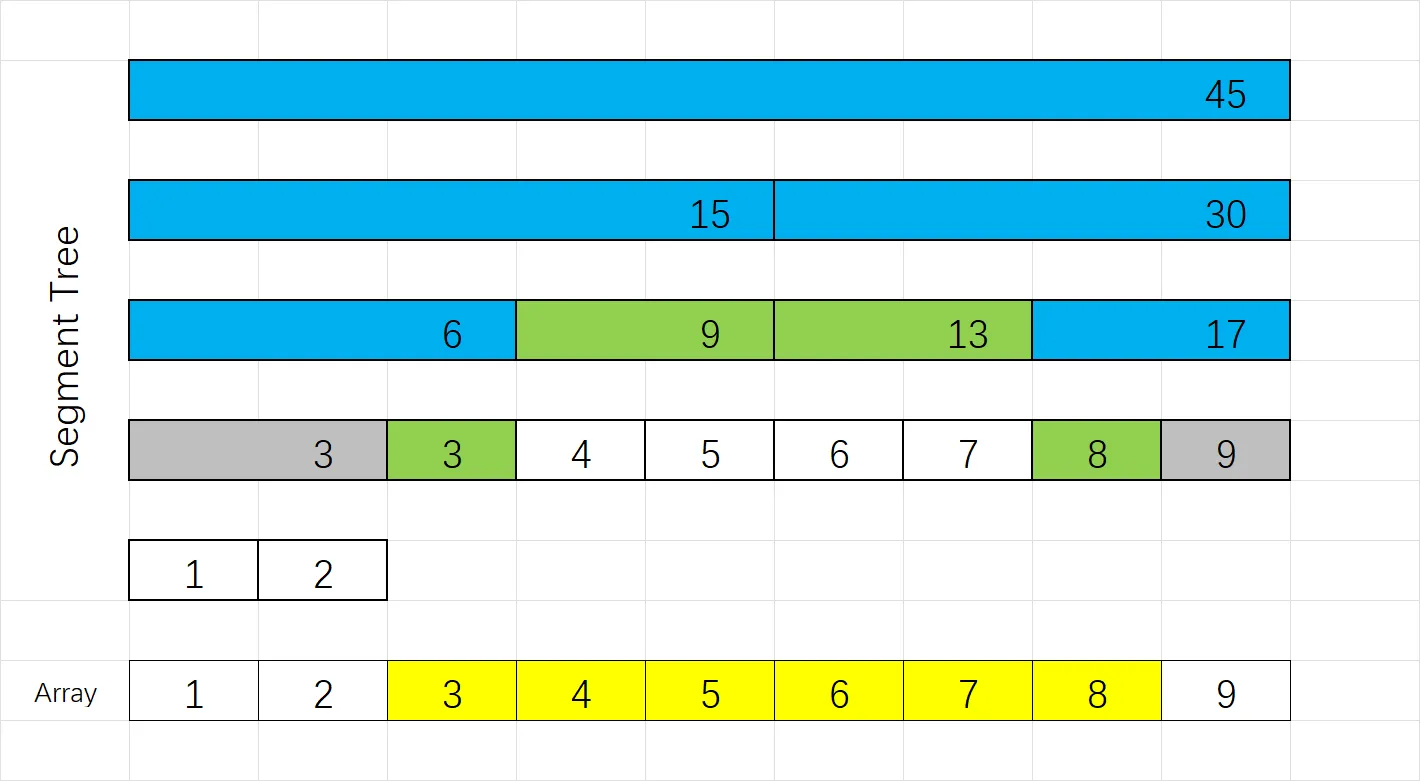
根据以上逻辑,同样使用递归实现区间查询功能,代码如下:
int query(int l, int r, int s, int t, int p)
{
if (l <= s && t <= r)
return sum[p];
int m = (s + t) / 2, ans = 0;
if (l <= m)
ans += query(l, r, s, m, p * 2);
if (r > m)
ans += query(l, r, m + 1, t, p * 2 + 1);
return ans;
}1.3 区间修改与懒惰标记
上面的代码纯粹是为了解释线段树的存储方式,压根没有包含修改操作,没有实用价值。接下来就要进入线段树最重要的部分,就是区间修改的内容了。
1.3.1 区间加法
若使用朴素的想法,要修改区间 $[l,r]$,则需要遍历 $[l,r]$ 区间内的所有节点,并将其修改。
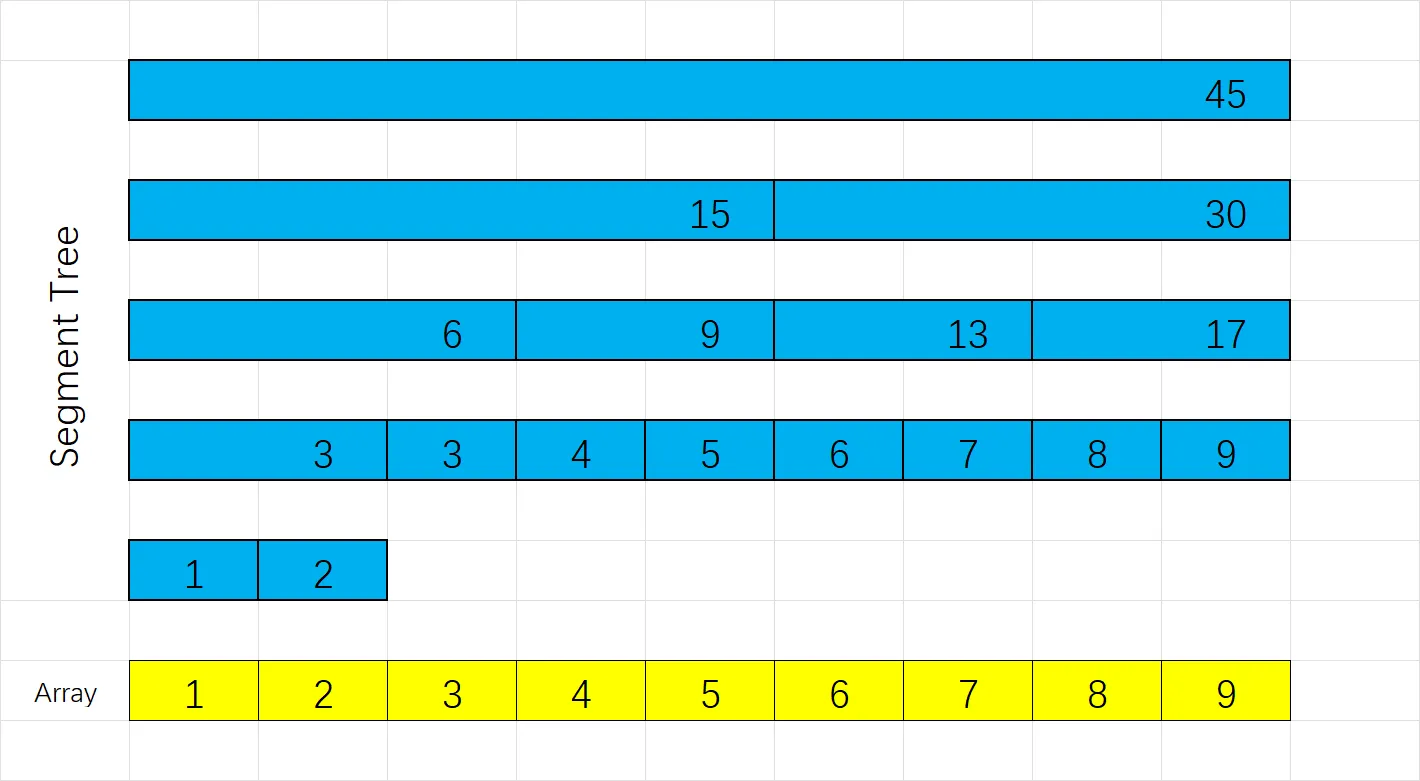
例如下面的情况,如果要修改整个区间(黄色),则所有节点(蓝色)都需要修改。如果这个线段树构成的完全二叉树深度很大,那么修改的时候需要修改的区间过多,时间复杂度无法满足。
为了解决这个问题,引入“懒惰标记”。进行修改时,并不真正修改对应区间的所有子区间,而是对节点打修改标记,标记节点对应的区间被修改。下一次访问带标记节点时,才进行真正的修改。这个操作相当于将现在需要立即完成的任务,平均到了未来进行完成,任务量更加平均。
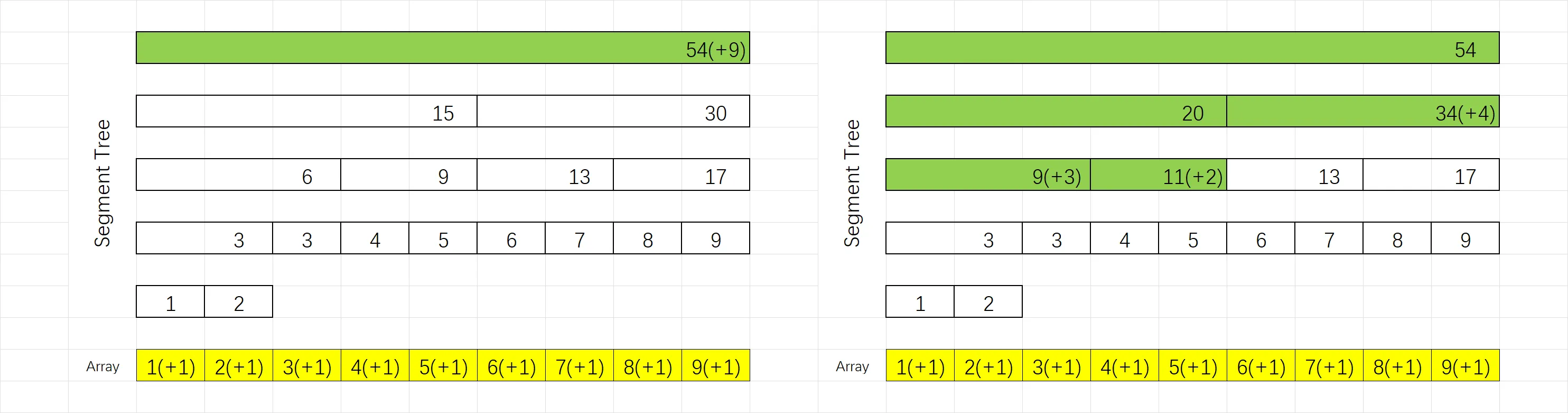
若使用“懒惰标记”,如果我们对整个区间 $+1$,修改操作时我们只会对 $[1,9]$ 节点进行真实修改,并在其上打上修改标记。如下图左,绿色为完成真实修改的节点,括号内为修改标记。
接下来,如果我们查询了 $[4,5]$ 这个节点,那么在查询过程中会考察到的节点全部都会被真实更新,如下图右,绿色的就是被真实更新的节点。同时修改标记发生了下传:原来的修改标记被去除,现在的修改标记位于二叉树最底部更新后的节点。
/* 线段树: 维护区间和, 支持区间加, 使用懒惰标记 */
/* 下标从1开始,注意空间大小 */
namespace segtree
{
constexpr int MAXN = 1e6;
int arr[MAXN], sum[MAXN]; // 原数组, 线段树区间和
int addv[MAXN]; // 加法实际值(同时做加法标记)
void push_down(int s, int t, int p)
{
if (addv[p] && s != t)
{
int m = (s + t) / 2;
sum[p * 2] += addv[p] * (m - s + 1);
sum[p * 2 + 1] += addv[p] * (t - m);
addv[p * 2] += addv[p];
addv[p * 2 + 1] += addv[p];
addv[p] = 0;
}
}
void push_up(int p)
{
sum[p] = sum[p * 2] + sum[p * 2 + 1];
}
void build(int s, int t, int p)
{
if (s == t)
{
sum[p] = arr[s];
return;
}
int m = (s + t) / 2;
build(s, m, 2 * p);
build(m + 1, t, 2 * p + 1);
push_up(p);
}
void add(int l, int r, int c, int s, int t, int p) // [l, r] += c
{
if (l <= s && t <= r)
{
sum[p] += (t - s + 1) * c;
addv[p] += c;
return;
}
push_down(s, t, p);
int m = (s + t) / 2;
if (l <= m)
add(l, r, c, s, m, p * 2);
if (r > m)
add(l, r, c, m + 1, t, p * 2 + 1);
push_up(p);
}
int query(int l, int r, int s, int t, int p) // [l, r] ?sum
{
if (l <= s && t <= r)
return sum[p];
push_down(s, t, p);
int m = (s + t) / 2, sum = 0;
if (l <= m)
sum += query(l, r, s, m, p * 2);
if (r > m)
sum += query(l, r, m + 1, t, p * 2 + 1);
return sum;
}
};1.3.2 区间修改
上面是对区间进行加法,线段树也可以完成将区间修改到指定值。
/* 线段树: 维护区间和, 支持区间修改, 使用懒惰标记 */
/* 下标从1开始,注意空间大小 */
namespace segtree
{
constexpr int MAXN = 1e6 + 10;
int arr[MAXN], sum[MAXN]; // 原数组, 线段树区间和
int updv[MAXN]; // 修改值
bool updt[MAXN]; // 修改标记
void push_down(int s, int t, int p)
{
if (updt[p] && s != t)
{
int m = (s + t) / 2;
sum[p * 2] = updv[p] * (m - s + 1);
sum[p * 2 + 1] = updv[p] * (t - m);
updv[p * 2] = updv[p];
updv[p * 2 + 1] = updv[p];
updt[p * 2] = 1;
updt[p * 2 + 1] = 1;
updt[p] = 0;
}
}
void push_up(int p)
{
sum[p] = sum[p * 2] + sum[p * 2 + 1];
}
void build(int s, int t, int p)
{
if (s == t)
{
sum[p] = arr[s];
return;
}
int m = (s + t) / 2;
build(s, m, 2 * p);
build(m + 1, t, 2 * p + 1);
push_up(p);
}
void update(int l, int r, int c, int s, int t, int p) // [l, r] = c
{
if (l <= s && t <= r)
{
sum[p] = (t - s + 1) * c;
updt[p] = 1;
updv[p] = c;
return;
}
push_down(s, t, p);
int m = (s + t) / 2;
if (l <= m)
update(l, r, c, s, m, p * 2);
if (r > m)
update(l, r, c, m + 1, t, p * 2 + 1);
push_up(p);
}
int query(int l, int r, int s, int t, int p) // [l, r] ?sum
{
if (l <= s && t <= r)
return sum[p];
push_down(s, t, p);
int m = (s + t) / 2, ans = 0;
if (l <= m)
ans += query(l, r, s, m, p * 2);
if (r > m)
ans += query(l, r, m + 1, t, p * 2 + 1);
return ans;
}
};1.3.3 区间加法和乘法
如果要让区间修改既支持加法,也支持乘法,那么首先肯定需要两种修改标记,因为加法和乘法的逻辑是不同的。我们用 $\text{add\_val}$ 记录加法标记,$\text{mul\_val}$ 来记录乘法标记。在初始化时,$\text{add\_val}_i=0,\; \text{mul\_val}_i=1$.
其次,在进行区间加和区间和的时候,乘法会影响到加法标记:
- 若对 $\mathrm{sum}_i$ 进行 $+c$ 操作:$\mathrm{sum}_i:=\mathrm{sum}_i+c\cdot(t-s+1)$
- 若对 $\mathrm{sum}_i$ 进行 $\times c$ 操作:$\mathrm{sum}_i:=c\cdot \mathrm{sum}_i$ 且 $\text{mul\_val}_i:=c\cdot \text{mul\_val}_i$
同时,在进行标记下传时,乘法和加法的计算顺序也非常重要,应当先乘再加。因为我们在 $\times c$ 的时候已经对加法标记同时 $\times c$ 了,如果再先加后乘的话,加法标记相当于 $\times c^2$,这样就不正确了。
如果一个节点 $\mathrm{sum}_i$ 有加法标记 $+x$ 和乘法标记 $\times y$,它在进行下传给左右子节点时,操作应该如下:
- 左子节点 $\mathrm{sum}_{2i}$:$\begin{cases}\mathrm{sum}_{2i}:=y\cdot \mathrm{sum}_{2i}+x\cdot(m-s+1)\\\text{add\_val}_{2i}:=y\cdot \text{add\_val}_{2i}+x\cdot(m-s+1)\\\text{mul\_val}_{2i}:=y\cdot \text{mul\_val}_{2i}\end{cases}$
- 右子节点 $\mathrm{sum}_{2i+1}$:$\begin{cases}\mathrm{sum}_{2i+1}:=y\cdot \mathrm{sum}_{2i+1}+x\cdot(t-m)\\\text{add\_val}_{2i+1}:=y\cdot \text{add\_val}_{2i+1}+x\cdot(t-m)\\\text{mul\_val}_{2i+1}:=y\cdot \text{mul\_val}_{2i+1}\end{cases}$
- 父节点 $\mathrm{sum}_i$:$\begin{cases}\text{add\_val}_i=0\\\text{mul\_val}_i=1\end{cases}$
/* 线段树: 维护区间和, 支持区间加与乘, 使用懒惰标记 */
/* 下标从1开始,注意空间大小 */
namespace segtree
{
constexpr int MAXN = 1e6 + 10;
int arr[MAXN], sum[MAXN]; // 原数组, 线段树区间和
int addv[MAXN], mulv[MAXN]; // 加法值, 乘法值(同时做标记)
void push_down(int s, int t, int p)
{
int m = (s + t) / 2;
if (mulv[p] != 1 && s != t)
{
sum[p * 2] *= mulv[p];
sum[p * 2 + 1] *= mulv[p];
addv[p * 2] *= mulv[p];
addv[p * 2 + 1] *= mulv[p];
mulv[p * 2] *= mulv[p];
mulv[p * 2 + 1] *= mulv[p];
mulv[p] = 1;
}
if (addv[p] != 0 && s != t)
{
sum[p * 2] += addv[p] * (m - s + 1);
sum[p * 2 + 1] += addv[p] * (t - m);
addv[p * 2] += addv[p];
addv[p * 2 + 1] += addv[p];
addv[p] = 0;
}
}
void push_up(int p)
{
sum[p] = sum[p * 2] + sum[p * 2 + 1];
}
void build(int s, int t, int p)
{
mulv[p] = 1;
if (s == t)
{
sum[p] = arr[s];
return;
}
int m = (s + t) / 2;
build(s, m, 2 * p);
build(m + 1, t, 2 * p + 1);
push_up(p);
}
void add(int l, int r, int c, int s, int t, int p) // [l, r] += c
{
if (l <= s && t <= r)
{
sum[p] += (t - s + 1) * c;
addv[p] += c;
return;
}
push_down(s, t, p);
int m = (s + t) / 2;
if (l <= m)
add(l, r, c, s, m, p * 2);
if (r > m)
add(l, r, c, m + 1, t, p * 2 + 1);
push_up(p);
}
void mul(int l, int r, int c, int s, int t, int p) // [l, r] *= c
{
if (l <= s && t <= r)
{
sum[p] *= c;
addv[p] *= c;
mulv[p] *= c;
return;
}
push_down(s, t, p);
int m = (s + t) / 2;
if (l <= m)
mul(l, r, c, s, m, p * 2);
if (r > m)
mul(l, r, c, m + 1, t, p * 2 + 1);
push_up(p);
}
int query(int l, int r, int s, int t, int p) // [l, r] ?sum
{
if (l <= s && t <= r)
return sum[p];
push_down(s, t, p);
int m = (s + t) / 2;
int ans = 0;
if (l <= m)
ans += query(l, r, s, m, p * 2);
if (r > m)
ans += query(l, r, m + 1, t, p * 2 + 1);
return ans;
}
};2 权值线段树
2.1 定义
对于普通线段树,我们都知道维护的是数组区间信息,例如区间和、区间最大 / 小值,维护的内容是数据本身。
而对于权值线段树,维护的是数组区间内数的个数信息,例如 $1$ 的个数、$2$ 的个数,维护的内容相当于许多桶。
因此,对比总结一下:
- 普通线段树:维护信息,按个数开空间,维护具体信息。
- 权值线段树:维护桶,按值域(可离散化处理),维护个数。
2.2 实现
权值线段树和线段树的原理是完全一样的,只是我们使用线段树的方式发生了变化。
权值线段树相当于有如下功能的线段树,甚至比普通线段树更简化:
- 单点 $+1$(即插入一个数,让它的个数 $+1$)
- 区间求和(即查询有几个数在对应区间的值域内)
/* 权值线段树 */
namespace segtree
{
constexpr int MAXN = 1e6;
int sum[MAXN]; // 数的个数
void build(int s, int t, int p)
{
if (s == t)
{
sum[p] = 0;
return;
}
int m = (s + t) / 2;
build(s, m, 2 * p);
build(m + 1, t, 2 * p + 1);
}
void update(int x, int s, int t, int p)
{
sum[p]++;
if (s == t)
return;
int m = (s + t) / 2;
if (x <= m)
update(x, s, m, p * 2);
else
update(x, m + 1, t, p * 2 + 1);
}
int query(int k, int s, int t, int p)
{
if (s == t)
return s;
int m = (s + t) / 2;
if (sum[p * 2] >= k)
return query(k, s, m, p * 2);
else
return query(k - sum[p * 2], m + 1, t, p * 2 + 1);
}
};模板题的解法:
constexpr int MAXN = 3e4 + 10;
void solve()
{
int n, k;
cin >> n >> k;
vector<int> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
sort(a.begin(), a.end());
a.erase(unique(a.begin(), a.end()), a.end());
segtree::build(1, MAXN, 1);
for (int i = 0; i < a.size(); i++)
segtree::update(a[i], 1, MAXN, 1);
int ans = segtree::query(k, 1, MAXN, 1);
if (ans == MAXN)
cout << "NO RESULT" << endl;
else
cout << ans << endl;
}2.3 离散化
上面的模板题正整数均小于 $3\times 10^4$,我们可以直接开一个值域大小的权值线段树,那如果值域范围到了 $10^9$ 级别呢?
显然,$10^9$ 级别的值域不可能直接开这么大的线段树了,但是如果题目数据数量较少,例如只有 $10^6$ 个数,很多值域都没有用到,完全没必要维护它们。因此我们可以用离散化的技巧节省空间。
离散化其实就是维护了一个映射,把不连续的稀疏数据转化成连续的数据。
比如我们要统计数据 $[1,1,1,6,100,100,19999,100000000]$ 的数目,不离散化就得开个 $10^7$ 大小的数组。通过离散化我们可以把它转为 $[0,0,0,1,2,2,3,4]$,只需要 $5$ 大小的数组就完成了。
根据这个例子,大家大概也知道怎么离散化了:排序并去重后二分即可
(上面那道模板题其实已经要求去重了,所有不用二分,直接取数组下标即可)
void solve()
{
int n, k;
cin >> n >> k;
vector<int> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
sort(a.begin(), a.end());
a.erase(unique(a.begin(), a.end()), a.end());
segtree::build(1, a.size() + 10, 1);
for (int i = 0; i < a.size(); i++)
segtree::update(i, 1, a.size() + 10, 1);
int id = segtree::query(k, 1, a.size() + 10, 1);
if (id > a.size())
cout << "NO RESULT" << endl;
else
cout << a[id] << endl;
}本文采用 CC BY-SA 4.0 许可,本文 Markdown 源码:Haotian-BiJi
模板题:luogu P3372【模板】线段树 1 add函数if()不应该是l >= s吗