Kruskal 重构树：维护图上两点间所有简单路径的最大边权的最小值 / 维护树上两点间路径的最大边权的数据结构。

（也可以维护图上两点间所有简单路径的最小边权的最大值 / 维护树上两点间路径的最小边权）

建树

考虑 Kruskal 算法过程：

  1. 将边按权重从小到大排序

  2. 重复进行下面操作：

    • 取出最小的一条边 $u\overset{w}\leftrightarrow v$

      • 如果加入这条边后不会成环：加入这条边。
      • 如果加入这条边后成环：跳过这条边，重复上一步操作。
  3. 若所有边全部考察完毕或已经生成出一棵树，则停止算法。

Kruskal 重构树是在上面这个过程同时建立的。重构树可以用一个链式前向星储存，此外还需要一个 $\text{val}_i$ 数组储存重构树的点权：

若选择了 $u\overset{w}\leftrightarrow v$ 这条边，则在重构树中添加一个新节点 $k$，节点权值 $\text{val}_k=w$，然后需要新增两条边：$k\to\text{find}(u)$ 和 $k\to\text{find}(v)$. 其中 $\text{find}(\cdot)$ 就是 Kruskal 算法里并查集的函数，另外，在生成重构树之外，Kruskal 算法的其他操作照做。

建树代码片段如下：

vector<array<int, 3>> edge(n + 10); // 0-u, 1-v, 2-w
for (int i = 1; i < n; i++)
    cin >> edge[i][0] >> edge[i][1] >> edge[i][2];
sort(edge.begin() + 1, edge.begin() + n, [](array<int, 3> a, array<int, 3> b) { return a[2] < b[2]; });
int pos = n + 1;
for (int i = 1; i < n; i++)
{
    auto &[u, v, w] = edge[i];
    int fa_u = find(u), fa_v = find(v);
    if (fa_u == fa_v)
        continue;
    krus[pos].push_back(fa_u);
    krus[pos].push_back(fa_v);
    val[pos] = w;
    fa[fa_u] = pos;
    fa[fa_v] = pos;
    pos++;
}

一个 Kruskal 重构树的示例，左图为原图，其中加粗边为生成树的边，右图为对应的 Kruskal 重构树，节点旁的数字为点权。

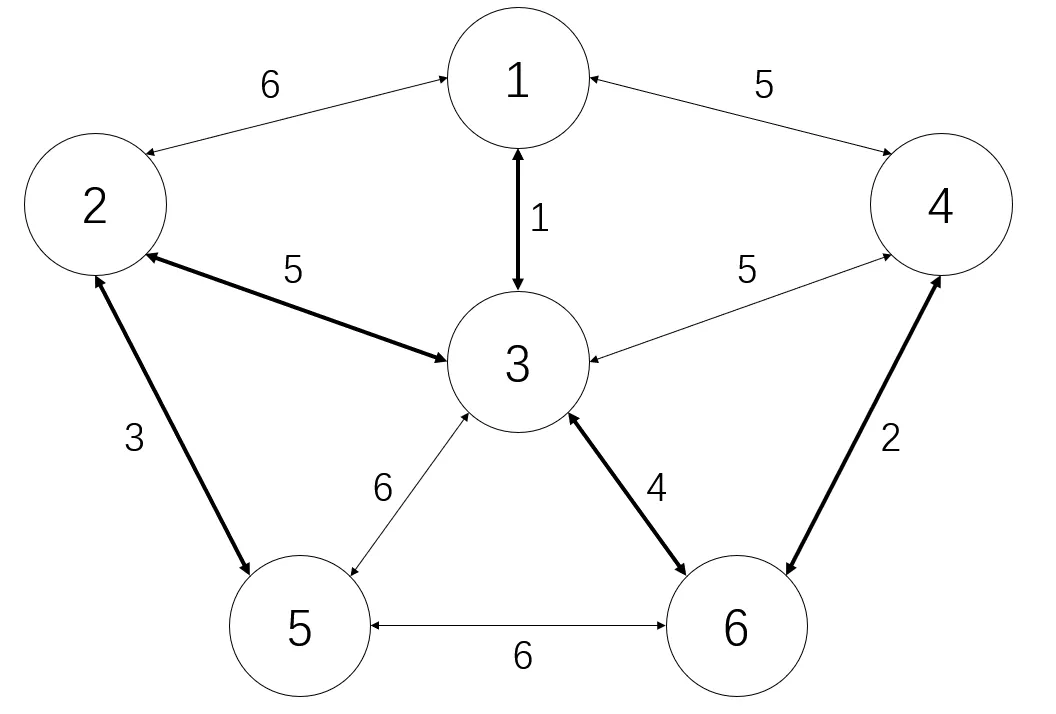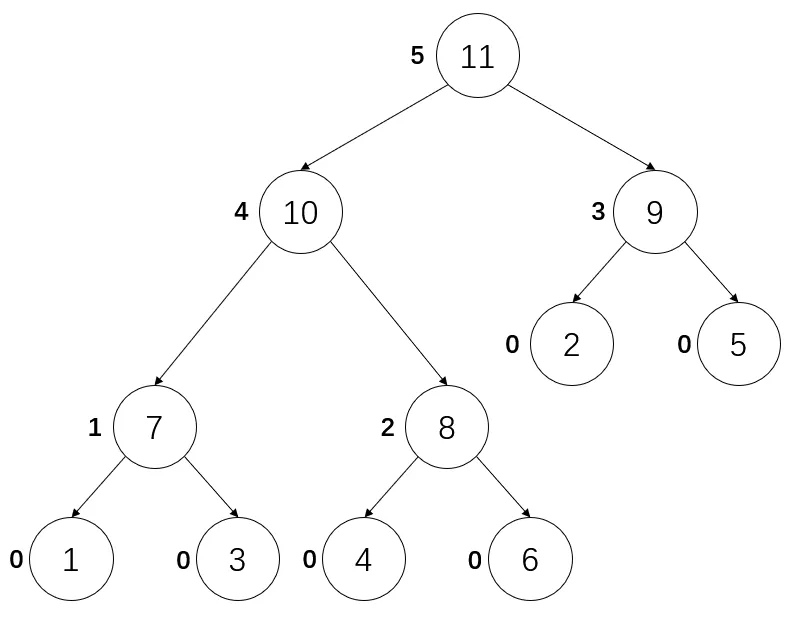性质

重构树中所有叶子节点为原图中的节点，重构树中所有内部节点为最小生成树中选择的边。

下面三个值大小相同：

  1. 原图中两个点之间的所有简单路径上最大边权的最小值
  2. 最小生成树上两个点之间的简单路径上的最大边权
  3. Kruskal 重构树上两点的最近公共祖先的点权

首先考虑 1, 2 两条，这两条其实是最小生成树的性质。两个点之间的所有简单路径上最大边权的最小值一定会被最小生成树取到，如果不取的话就不能保证最小了。

然后考虑 2,3 两条，Kruskal 建立最小生成树的每一步，相当于将两个集合合并，且连接这两个集合的的大小一定 $\geq$ 两个集合里面的边，这个是 Kruskal 从小到大选边保证的。那么两个节点如果一个在左集合，一个在右集合，它们的最短路径肯定要跨越这个连接两个集合的边，在 Kruskal 重构树内，这个就是两个节点的 LCA，权值就是 LCA 的点权。

注

上述建树时和 Kruskal 计算最小生成树一致，维护的是图上两点间所有简单路径的最大边权的最小值。

如果将边从大到小排序，即相当于计算最大生成树，此时维护的是图上两点间所有简单路径的最小边权的最大值。