求最小生成树（适合稀疏图）：Kruskal (克鲁斯卡尔) 算法

• 最小生成树是一副连通加权无向图中一棵权值最小的生成树。

Kruskal 算法

时间复杂度

时间复杂度：$O(\left|E\right|\log\left|V\right|)$

$\left|E\right|$ 为边数，$\left|V\right|$ 为顶点数，该版本适合稀疏图，即 $\left|E\right|\ll\left|V\right|^2$ 的图。

代码实现

const int MAXN = 1e5 + 10, INF = 0x3f3f3f3f;
int v, e;     // v顶点数 e边数
int fa[MAXN]; // 并查集
struct Edge   // 边的结构体，重载了<供sort()
{
    int start, end, dist;
    bool operator<(const Edge &x) const
    {
        return dist < x.dist;
    }
};
vector<Edge> edges; // 邻接表存边

inline void init(int n)
{
    for (int i = 1; i <= n; i++)
        fa[i] = i;
}

int find(int x)
{
    return x == fa[x] ? x : (fa[x] = find(fa[x]));
}

inline void merge(int i, int j)
{
    fa[find(i)] = find(j);
}

int kruskal()
{
    sort(edges.begin(), edges.end());
    int ans = 0, selected = 0;
    bool flag = false;
    for (auto ed : edges)
    {
        if (find(ed.start) != find(ed.end))
        {
            merge(ed.start, ed.end);
            ans += ed.dist;
            if (++selected == v - 1)
            {
                flag = true;
                break;
            }
        }
    }
    return flag ? ans : INF;
}

分析

该算法的核心思想就是：选择 $A$ 的边集合外，权值最小且不会成环的边，加入到 $A$ 中。

实现“选择 $A$ 的边集合外”的方法：将边排序，从小到大有序选择。

实现“权值最小”的方法：将边储存在 vector 内，按长度排序（我用的重载运算符和 sort() )

实现“不会成环”的方法：判断两节点是否已经联通，若已经联通，再加一条边肯定会成环，只有不连通才能合并（我用的并查集）。

下面用例子模拟一下该算法的过程：

初始化并查集：

将每个节点指向自身，图中用不同颜色表示。

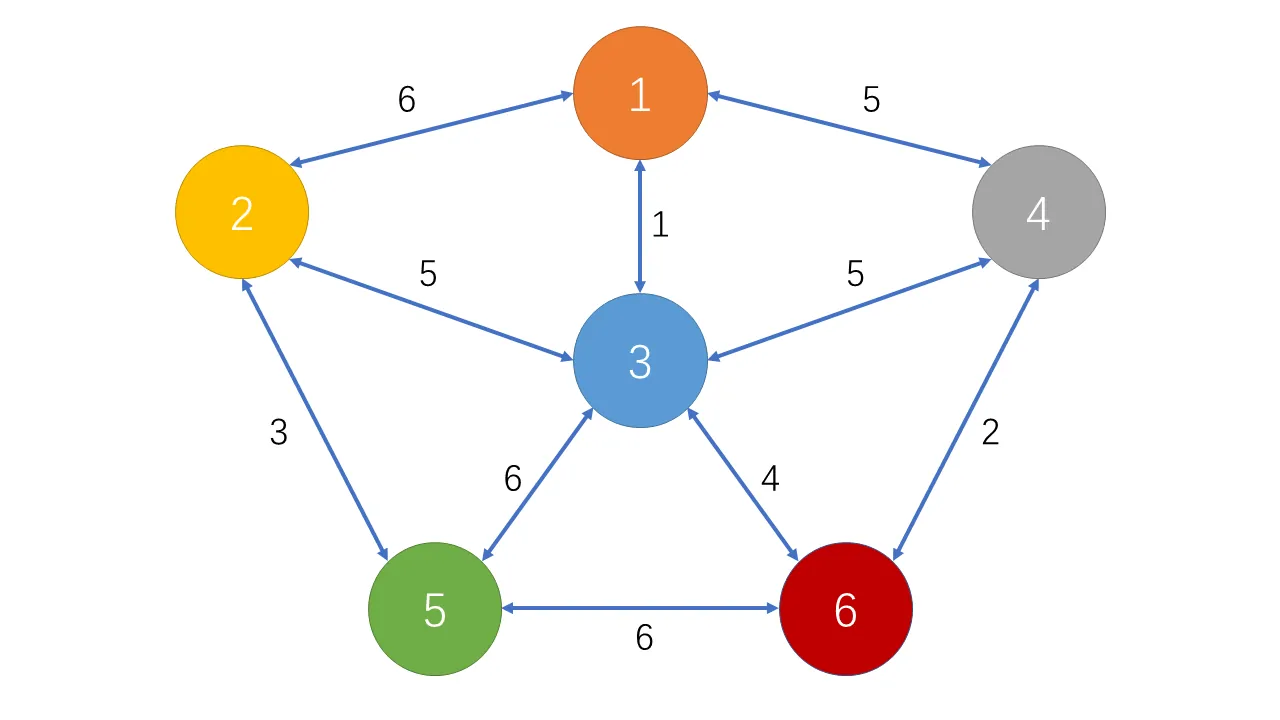
找到最短的边 $1\leftrightarrow 3$，长度为 $1$：

$fa[1]\neq fa[3]$，不会成环。将 $1$、$3$ 节点合并。

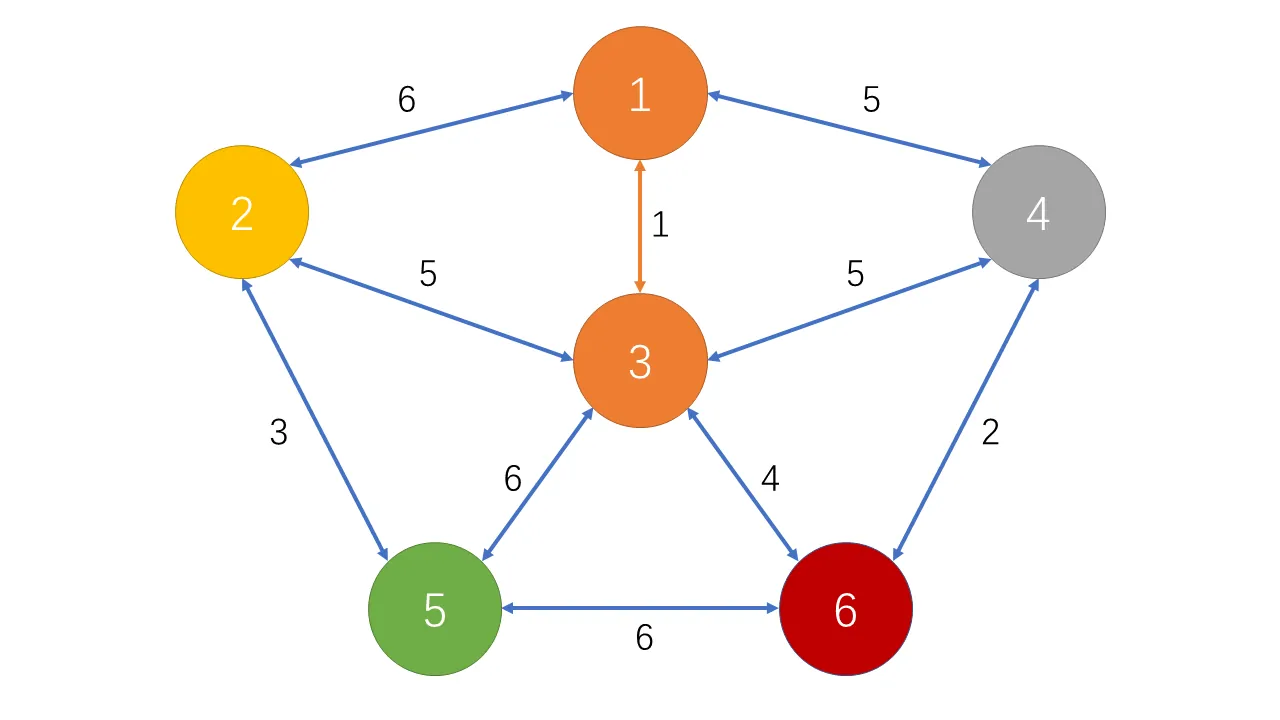
找到最短的边 $4\leftrightarrow 6$，长度为 $2$：

$fa[4]\neq fa[6]$，不会成环。将 $4$、$6$ 节点合并。

找到最短的边 $2\leftrightarrow 5$，长度为 $3$：

$fa[2]\neq fa[5]$，不会成环。将 $2$、$5$ 节点合并。

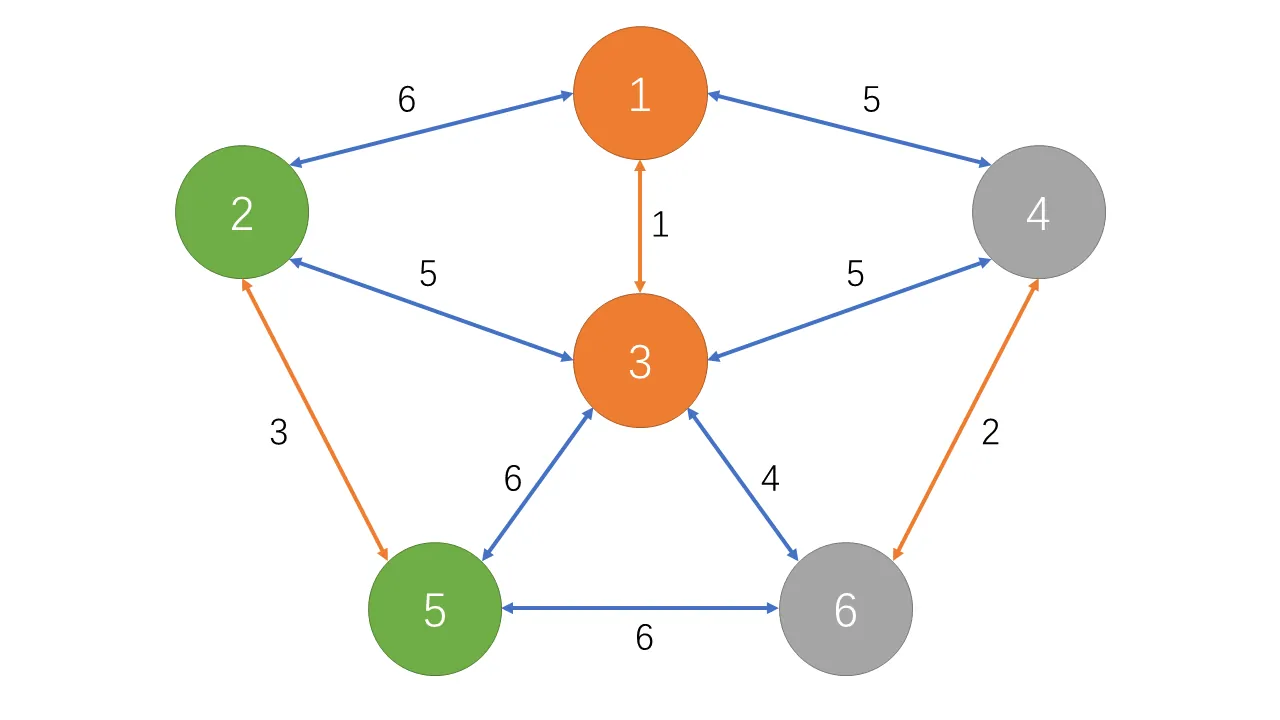
找到最短的边 $3\leftrightarrow 6$，长度为 $4$：

$fa[3]\neq fa[6]$，不会成环。将 $3$、$6$ 节点合并。

找到最短的边 $1\leftrightarrow 4, 3\leftrightarrow 4, 2\leftrightarrow 3$，长度为 $5$：

$fa[1]=fa[4], fa[3]=fa[4]$，会成环。不可合并。

$fa[2]\neq fa[3]$，不会成环。将 $2$、$3$ 节点合并。

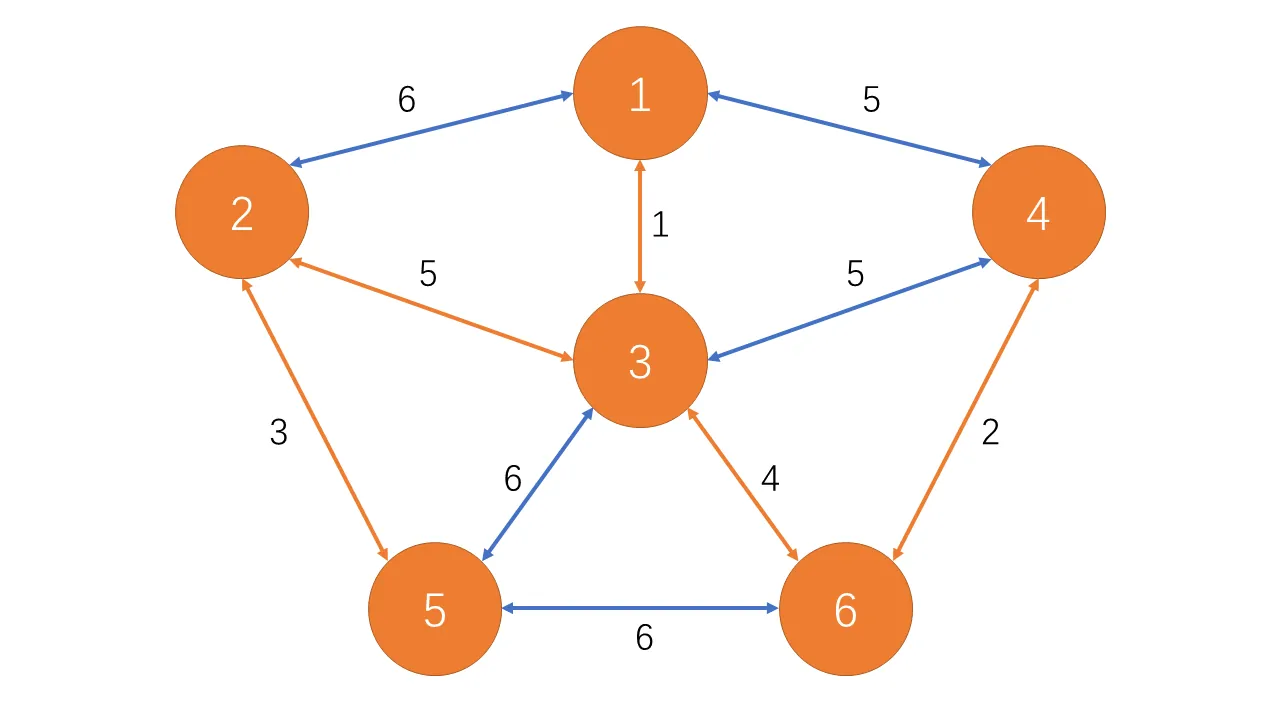
这时已经求出了最小生成树，后续操作均会成环，因此都会被跳过。