归并树 (Merge Sort Tree): 归并树是线段树和归并排序的合成，它利用线段树将归并排序的每一步都记录下来。

  • 查找区间 $[l,r]$ 内的大小范围在 $[a,b]$ 的数的个数（类似条件均可查找）
  • 查找区间 $[l,r]$ 内第 $k$ 大的数

归并树的思想基于线段树，因此需要先学习线段树：https://io.zouht.com/117.html

思路

归并排序我们不陌生，核心思想就是用递归完成拆分和合并。观察归并的拆分方式，我们可以发现，它和线段树完全一样。

下图是线段树的分段示意图，如果我们把它看作归并排序的拆分过程，可以发现其实是一模一样的。

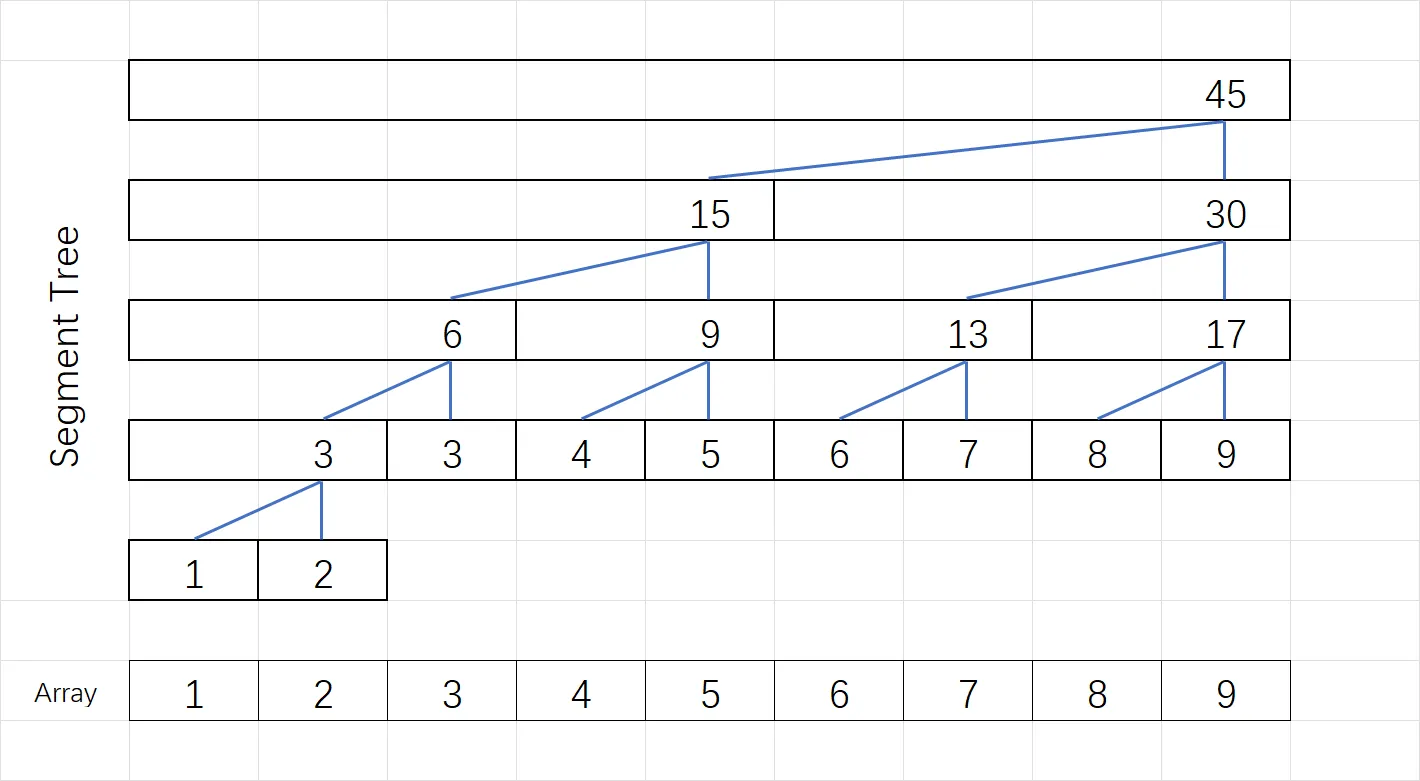
线段树中，每个节点储存的是一个数值，这个数值维护着这一段的信息。

而归并树中，每个节点储存的是一个有序数列，这个数列就是归并到该节点时的有序数列状态。其实就是利用线段树将归并排序的每一步都记录下来。

应用

查找区间 $[l,r]$ 内的 $\leq x$ 的数的个数

思想和线段树的区间查询完全一致：

由长分解到短，对于长度为 $n$ 的数列，初始时考察区间为全体：$s=1,t=n$.

  • 如果线段树内的区间 $[s,t]$ 完全被 $[l,r]$ 包含，在该节点的有序数列中二分找到 $\leq x$ 的数的个数，加入答案。

  • 否则，则考察它的左右子区间，令分界点 $m=\lfloor\frac{s+t}{2}\rfloor$：

    • 如果 $[s,t]$ 的左子区间 $[s,m]$ 与 $[l,r]$ 有交集（$l\leq m$）

      • 递归考察 $[s,m]$ 区间

    • 如果 $[s,t]$ 的右子区间 $[m+1,t]$ 与 $[l,r]$ 有交集（$m+1\leq r$）

      • 递归考察 $[m+1,t]$ 区间
  • 如果上面的情况都不满足，则说明 $[s,t]$ 区间与我们要求的 $[l,r]$ 区间完全不相交，直接跳过。

对于找 $<x$ / $>x$ / $\geq x$ 的数的个数，调整符号即可。对于找 $\in[a,b]$ 的数的个数，将 $\leq b$ 的个数减去 $<a$ 的个数即可。

查找区间 $[l,r]$ 内第 $k$ 大的数

我们在最终的有序数列 $res$ 中二分，初始时 $pl=1,pr=n$：

  • 如果 $pl<pr$ 则执行：

    • 中点 $mid=(pl+pr)/2$

    • 如果查询 $[l,r]$ 中 $\leq res_{mid}$ 的数的个数 $<k$

      • 令 $pl = mid + 1$

    • 如果查询 $[l,r]$ 中 $\leq res_{mid}$ 的数的个数 $\geq k$

      • 令 $pr=mid$
  • 最终，第 $k$ 大的数便是 $res_l$.

其中，最终的有序数列 $res$ 其实就是线段树根节点储存的序列。

代码

  • 建树：$O(n\log n)$
  • 查范围数量：$O(\log^2 n)$
  • 查第 $k$ 小：$O(\log^3 n)$
struct MergeSortTree
{
    /* ### array index must start from ONE ### */
    int n;
    vector<vector<int>> tree;

    // arr: ori arr, [s, t]: cur seg, x: cur node
    void build(const vector<int> &arr, int s, int t, int x)
    {
        if (s == t)
        {
            tree[x] = {arr[s]};
            return;
        }
        int m = (s + t) / 2;
        build(arr, s, m, 2 * x);
        build(arr, m + 1, t, 2 * x + 1);
        merge(tree[2 * x].begin(), tree[2 * x].end(),
              tree[2 * x + 1].begin(), tree[2 * x + 1].end(),
              back_inserter(tree[x]));
    }

    MergeSortTree(const vector<int> &arr) : n(arr.size())
    {
        int sz = 1 << (__lg(n) + bool(__builtin_popcount(n) - 1)); // sz = \lceil \log_{2}{n} \rceil
        tree.resize(2 * sz);
        build(arr, 1, n, 1);
    }

    // [l, r]: query array interval, [mn, mx]: query value interval, [s, t]: cur seg, x: cur node
    int count(int l, int r, int mn, int mx, int s, int t, int x)
    {
        if (l <= s && t <= r)
            return upper_bound(tree[x].begin(), tree[x].end(), mx) - lower_bound(tree[x].begin(), tree[x].end(), mn);
        int m = (s + t) / 2, ans = 0;
        if (l <= m)
            ans += count(l, r, mn, mx, s, m, x * 2);
        if (r > m)
            ans += count(l, r, mn, mx, m + 1, t, x * 2 + 1);
        return ans;
    }

    // query number of elements in the [l, r] interval that fall within the range [mn, mx]
    int count(int l, int r, int mn, int mx)
    {
        return count(l, r, mn, mx, 1, n, 1);
    }

    // find the kth smallest number in the [l, r] interval
    int count(int l, int r, int k)
    {
        int pl = 1, pr = n;
        while (pl < pr)
        {
            int mid = (pl + pr) / 2;
            if (count(l, r, INT32_MIN, tree[1][mid]) < k)
                pl = mid + 1;
            else
                pr = mid;
        }
        return tree[1][pl];
    }
};

模板题

Luogu P3834: https://www.luogu.com.cn/problem/P3834

(该题应当用复杂度更优的可持久化线段树来完成，用本文的归并树应当只能 AC 五个点)