莫队算法适用于：若存在一个长度为 $n$ 的序列，对于序列上的 $m$ 个区间询问问题，如果一个区间答案能够在 $O(1)$ 转移到相邻区间的答案，那么可以通过莫队算法在 $O(n\sqrt m)$ 的复杂度求出所有询问。

对于区间 $[l,r]$，它的相邻区间定义为：

$[l-1,r]$
$[l+1,r]$
$[l,r-1]$
$[l,r+1]$

普通莫队

原理

将所有询问区间 $[l,r]$ 离线后排序，首先按第一关键字 $l$ 排序，然后按第二关键字 $r$ 排序。然后按顺序处理询问，对于首个区间询问的答案，通过暴力计算取得。之后的答案基于上一个区间 $[l,r]$ 的答案，通过暴力一步一步转移，得到下一个区间 $[l',r']$ 的答案。

代码框架如下：

int cur_ans = 0; // current answer
void add(int pos) { /* update current answer */ }
void del(int pos) { /* update current answer */ }

void solve()
{
    sort(query.begin(), query.end());
    int l = 1, r = 0; // initial
    for (int i = 0; i < m; i++)
    {
        while (l > query[i].l) add(--l);
        while (r < query[i].r) add(++r);
        while (l < query[i].l) del(l++);
        while (r > query[i].r) del(r--);   
        ans[query[i].idx] = cur_ans;
    }
}

每一次转移时包含了四个循环，需要注意循环的顺序很关键，随意修改可能会导致错误。循环排列顺序共 $24$ 种，其中只有 $6$ 种是正确的，上面则为其中一种：l--, r++, l++, r--

之所以有些顺序是错误的，是因为它们会导致 $l>r+1$ 的情况，这将导致元素加入次数为负数，产生异常。

上面这种的正确性可以这样思考，l--, r++ 首先将区间扩大，l++, r-- 然后将区间缩小直到缩小为 $[l',r']$ ，全程可以保证 $l\leq r+1$.

优化

考虑一种询问情况，排序后如下：

我们模拟一下上面的情况，可以发现总移动次数约为 $3000$ 次，左右指针的移动过程如下图：

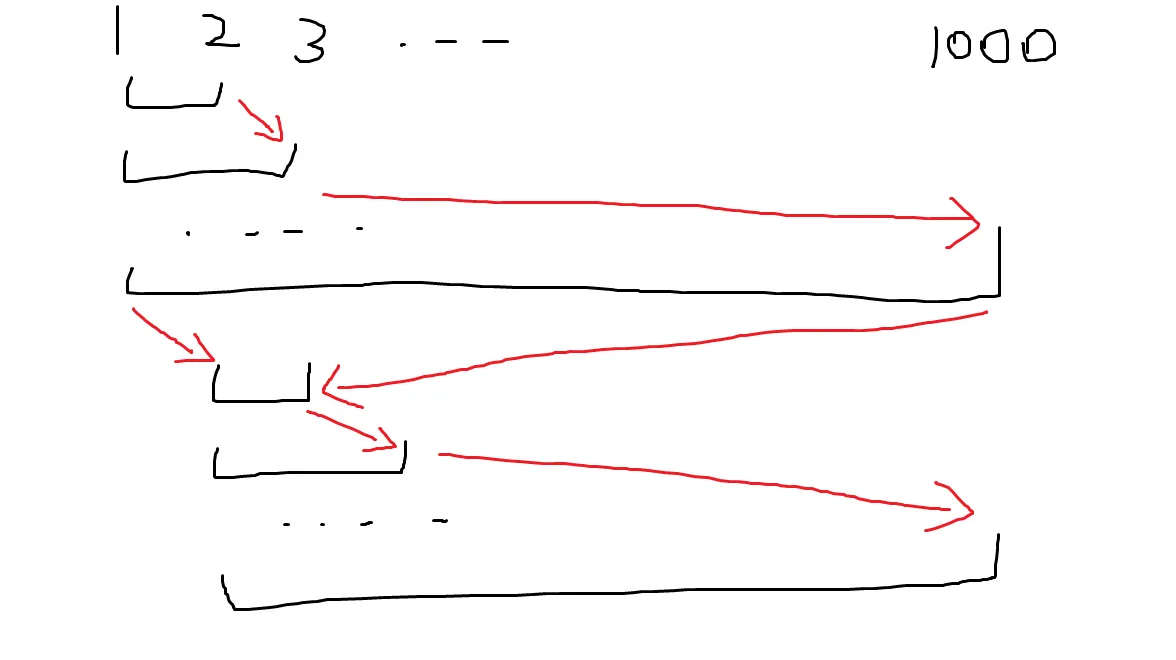
从 $l=1$ 到 $l=2$ 的转换过程中，$r$ 指针从 $1000$ 左移到 $3$，在 $l=2$ 的区间计算过程中，$r$ 指针又从 $3$ 左移到了 $1000$.

我们可以很明显的发现，$r$ 指针浪费了很多时间，它完全可以在从右往左返回时顺便把 $l=2$ 的询问给计算了，过程如下：

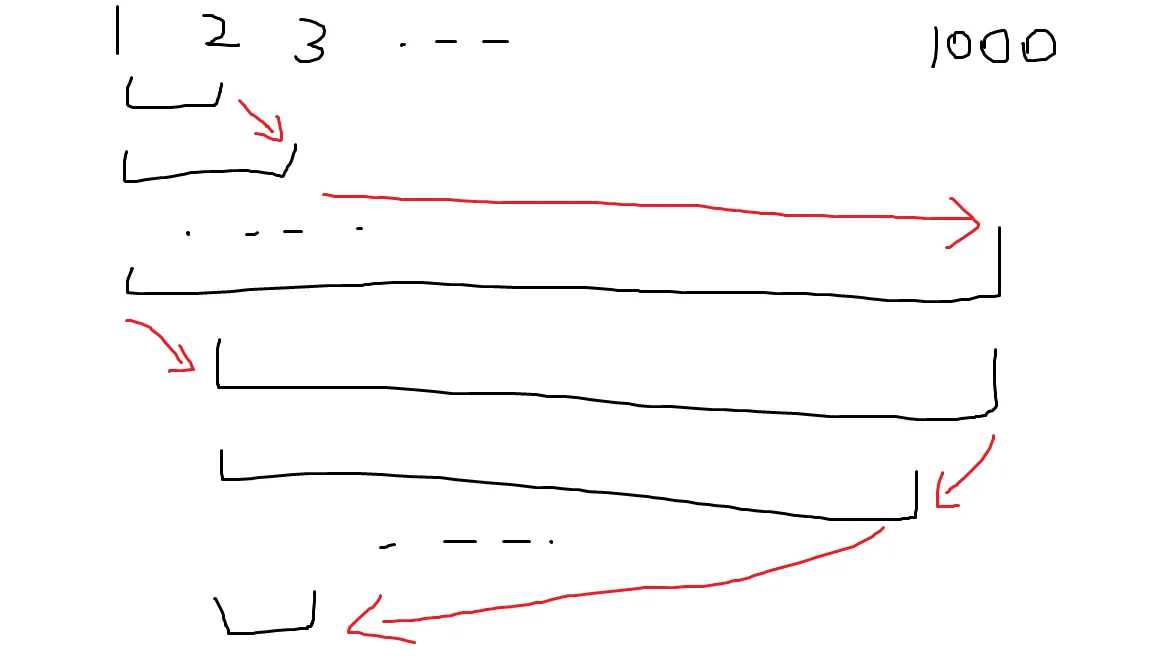
可以发现，如果按优化后的策略，总移动次数约为 $2000$ 次，优化程度高达约 $33\%$.

将上面的思路转化为代码实现，流程即为：

设块长度为 $S$，则可以将 $m$ 个区间分为 $\frac{m}{S}$ 个块
在每一块中分别排序：
- 对于编号奇数的块：第一关键字 $l$ 升序，第二关键字 $r$ 升序
- 对于编号偶数的块：第一关键字 $l$ 升序，第二关键字 $r$ 降序

取 $S=\sqrt m$ 时最佳。

转换成 cmp 函数则为：

int block;
bool cmp(Query a, Query b)
{
    if (a.l / block != b.l / block)
        return a.l < b.l;
    return (a.l / block) % 2 ? a.r < b.r : a.r > b.r;
}

上面的例子虽说是一个构造的特例，但是实际上一般情况，这种优化也是能让程序快 $30\%$ 左右的。

例题

模板题：[Luogu P1494 [国家集训队] 小 Z 的袜子](https://www.luogu.com.cn/problem/P1494)

constexpr int MAXN = 5e4 + 10;
int n, m, block;
int c[MAXN], cnt[MAXN];
pair<int, int> ans[MAXN];

struct Query
{
    int id, l, r;

    bool operator<(Query b)
    {
        if (l / block != b.l / block)
            return l < b.l;
        return (l / block) % 2 ? r < b.r : r > b.r;
    }
};

Query qu[MAXN];

int cur = 0;
void add(int x)
{
    cur += cnt[x];
    cnt[x]++;
}

void del(int x)
{
    cnt[x]--;
    cur -= cnt[x];
}

void solve()
{
    cin >> n >> m;
    block = sqrt(n);
    for (int i = 1; i <= n; i++)
        cin >> c[i];
    for (int i = 1; i <= m; i++)
    {
        cin >> qu[i].l >> qu[i].r;
        qu[i].id = i;
    }
    sort(qu + 1, qu + 1 + m);
    int l = 1, r = 0;
    for (int i = 1; i <= m; i++)
    {
        if (qu[i].l == qu[i].r)
            continue;
        while (l > qu[i].l) add(c[--l]);
        while (r < qu[i].r) add(c[++r]);
        while (l < qu[i].l) del(c[l++]);
        while (r > qu[i].r) del(c[r--]);
        ans[qu[i].id] = {cur, (r - l + 1) * (r - l) / 2};
    }
    for (int i = 1; i <= m; i++)
    {
        auto &[a, b] = ans[i];
        if (a == 0)
            b = 1;
        int g = gcd(a, b);
        cout << a / g << '/' << b / g << endl;
    }
}

用莫队的关键点就是找相邻区间的递推方式，对于本题来说，区间的变化分为两种：变长、变短。

如果区间变长（l-- / r++），则代表区间会加入颜色为 $c_x$ 的这双袜子，如果这双袜子在原区间内有 $\text{cnt}(c_x)$ 双，分子（合法选法总数）的变化则为：

$$ ans_{\text{new}} = ans_{\text{old}} + \binom{\text{cnt}(c_x)+1}{2} - \binom{\text{cnt}(c_x)}{2} = ans_{\text{old}} + \text{col}(c_x) $$

注意同时更新 $\text{cnt}(c_x)$ 的数目。除以分母（选法总数）便得到了这个询问的答案：

$$ \frac{ans}{\binom{r-l+1}{2}} $$

那么相反，如果区间变短（l++ / r--），则代表区间会去掉颜色为 $c_x$ 的这双袜子，符号反过来即可：

$$ ans_{\text{new}} = ans_{\text{old}} - \binom{\text{cnt}(c_x)}{2} + \binom{\text{cnt}(c_x) - 1}{2} = ans_{\text{old}} - (\text{col}(c_x) - 1) $$

带修改莫队

对于一个同区间修改，如果我们能在 $O(1)$ 的速度从原答案转移到它，那么带修改的莫队可以解决这个问题。

原理

对于修改，我们也将它看作和左右端点一样的维度。左右端点移动可以递推，那修改前后的版本也当然可以递推。

原来的询问格式为 $[l,r]$，那么带修改的格式为 $[l,r,ver]$. 对于该区间，可以递推到：

$[l-1,r,ver]$
$[l+1,r,ver]$
$[l,r-1,ver]$
$[l,r+1,ver]$
$[l,r,ver-1]$
$[l,r,ver+1]$

对于新问题，排序方式为：第一关键字 $l$ 升序，第二关键字 $r$ 升序，第三关键字 $ver$ 升序。

那么递推步骤便是，首先将左右端点从 $[l,r]$ 暴力移动到 $[l',r']$. 如果版本没有变化那这就是答案；如果变化 $ver\to ver'$ 变新，那需要执行修改并维护答案；如果变化 $ver\to ver'$ 变旧，那需要还原修改并维护答案。

具体难点在于修改的加减，如果版本变新 $ver_i\to ver_j$，那么对于修改 $i\sim j$ 需要进行：

执行修改：在原序列上执行修改，但要注意的是需要保存原值（代码直接用 swap 来实现），便于还原修改。
维护答案：如果修改点 $pos\in[l,r]$，那么需要根据修改转移答案，反之不用操作。

如果版本变旧 $ver_j\to ver_i$，那么对于修改 $i\sim j$ 需要进行：

还原修改：还序列上的修改，但要注意的是需要保存修改值（代码直接用 swap 来实现），便于执行修改。
维护答案：如果修改点 $pos\in[l,r]$，那么需要根据还原转移答案，反之不用操作。

例题

模板题：[Luogu P1903 [国家集训队] 数颜色 / 维护队列](https://www.luogu.com.cn/problem/P1903)

constexpr int MAXN = 2e5 + 10, MAXM = 1e6 + 10;
int n, m, block;
int c[MAXN], ans[MAXN], cnt[MAXM];

struct Query
{
    int idx, l, r, ver;

    bool operator<(Query b)
    {
        if (l / block != b.l / block)
            return l < b.l;
        else if (r / block != b.r / block)
            return r < b.r;
        else
            return ver < b.ver;
    }
};

struct Modif
{
    int pos, color;
};

Query qu[MAXN];
Modif mo[MAXN];

int cur = 0;
void add(int x)
{
    if (cnt[x] == 0)
        cur++;
    cnt[x]++;
}

void del(int x)
{
    cnt[x]--;
    if (cnt[x] == 0)
        cur--;
}

void solve()
{
    cin >> n >> m;
    block = pow(n, 2.0 / 3);
    for (int i = 1; i <= n; i++)
        cin >> c[i];
    int now_idx = 0, now_ver = 0;
    for (int i = 1; i <= m; i++)
    {
        string op;
        int x, y;
        cin >> op >> x >> y;
        if (op == "Q")
            qu[++now_idx] = {now_idx, x, y, now_ver};
        else // if (op == "R")
            mo[++now_ver] = {x, y};
    }
    sort(qu + 1, qu + 1 + now_idx);
    int l = 1, r = 0, time = 0;
    for (int i = 1; i <= now_idx; i++)
    {
        while (l > qu[i].l) add(c[--l]);
        while (r < qu[i].r) add(c[++r]);
        while (l < qu[i].l) del(c[l++]);
        while (r > qu[i].r) del(c[r--]);
        while (time < qu[i].ver)
        {
            time++;
            if (l <= mo[time].pos && mo[time].pos <= r)
            {
                add(mo[time].color);
                del(c[mo[time].pos]);
            }
            swap(mo[time].color, c[mo[time].pos]);
        }
        while (time > qu[i].ver)
        {
            if (l <= mo[time].pos && mo[time].pos <= r)
            {
                add(mo[time].color);
                del(c[mo[time].pos]);
            }
            swap(mo[time].color, c[mo[time].pos]);
            time--;
        }
        ans[qu[i].idx] = cur;
    }
    for (int i = 1; i <= now_idx; i++)
        cout << ans[i] << endl;
}

注意事项：对于上一题的莫队来说，我们向 add() / del() 传入的是下标值，但对于本题来说，我们向 add() / del() 传入的是具体的颜色值。原因是我们在执行修改时，如果用下标传值没法完成颜色的修改，因为待修改值根本就不在原序列中，没有下标这个概念。

算法 | 莫队算法

普通莫队

原理

优化

例题

带修改莫队

原理

例题

添加新评论

最新文章

分类

标签

其它