隐马尔可夫模型 (Hidden Markov Model): 一种统计模型，用来描述一个含有隐含未知参数的马尔可夫过程。

1 模型实例

首先用一个具体的实例来初步了解隐马尔可夫模型。

有 $3$ 个桶，每个桶有 $3$ 种颜色（R, G, B）的球，每个桶内球的数量不同：

第一步：选取初始桶

我们有一个初始概率分布，随机从 $3$ 个桶内选取一个作为初始桶：

第二步：根据目前选取的桶，随机在其中抽取一个球

由于每个桶内球的数量不同，因此抽出球的颜色的概率不同。如果目前在 $3$ 号桶，那么抽出来颜色的概率如下：

第三步：根据目前选取的桶，随机转移到另一个桶

我们有一个转移概率矩阵，根据矩阵进行桶的转移：

例如，如果目前在桶 $3$，那么转移到桶 $1$ 的概率为 $40\mathrm{\%}$.

第四步：回到第二步，循环重复这个过程。

以上，便是隐马尔可夫模型的一个具体实例。具体来说，便是：

• 状态空间 $\mathcal{Y}=\{\mathrm{桶}1,\mathrm{桶}2,\mathrm{桶}3\}$
• 观测变量 $\mathcal{X}=\{R,G,B\}$
• 初始状态概率 $\mathit{\pi }=(0.3,0.2,0.5)$
• 状态转移概率 $\mathit{A}=\left[\begin{array}{ccc}0.1& 0.3& 0.6\\ 0.2& 0.5& 0.3\\ 0.4& 0.2& 0.4\end{array}\right]$
• 输出观测概率 $\mathit{B}=\left[\begin{array}{ccc}0.33& 0.33& 0.33\\ 0.17& 0.33& 0.5\\ 0.3& 0.5& 0.2\end{array}\right]$

2 数学定义

隐马尔可夫模型有两个空间：

• 系统状态空间 $\mathcal{Y}=\{s_1,s_2,\dots ,s_N\}$
• 观测变量空间 $\mathcal{X}=\{o_1,o_2,\dots ,o_M\}$

隐马尔可夫模型有两组变量：

• 状态变量（隐变量）$\{y_1,y_2,\dots ,y_n\}$ ：$y_i\in \mathcal{Y}$ 是系统在 $i$ 时刻的状态
• 观测变量 $\{x_1,x_2,\dots ,x_n\}$。：$x_i\in \mathcal{X}$ 是系统在 $i$ 时刻的观测值

隐马尔可夫模型有两个假设：

• 齐次性假设：$t$ 时刻状态 $y_t$ 仅依赖于 $t-1$ 时刻的状态 $y_{t-1}$.
• 观测独立性假设：观测变量的取值仅依赖于状态变量，与其他状态变量与观测变量无关，即 $x_t$ 仅由 $y_t$ 确定。

除了上述结构，隐马尔可夫模型还包含三个参数，含义不再解释：

• 初始状态概率 $\mathit{\pi }$：${\pi }_i=P(y_1=i)$
• 状态转移概率 $\mathit{A}$​：$a_{ij}=P(y_{t+1}=j\mid y_t=i)$
• 输出观测概率 $\mathit{B}$：$b_i(j)=P(x_t=j\mid y_t=i)$

综上，一个隐马尔可夫模型可以由一个三元组表示：

$$\lambda =(\mathit{A},\mathit{B},\mathit{\pi })$$

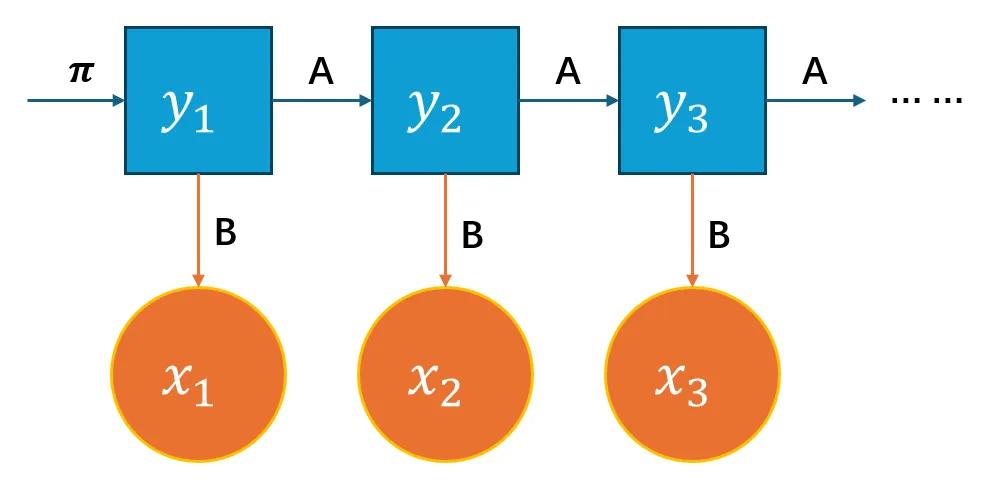
它按以下过程产生观测序列 $\{x_1,x_2,\dots ,x_n\}$：

1. 设置 $t=1$，根据初始状态概率 $\mathit{\pi }$ 选择初始状态 $y_1$
2. 根据状态 $y_t$ 和输出观测概率 $\mathit{B}$ 产生观测变量 $x_t$
3. 根据状态 $y_t$ 和状态转移概率 $\mathit{A}$ 转移模型状态到 $y_{t+1}$
4. 若 $t<n$ 则令 $t\leftarrow t+1$ 并跳到第 $2$​ 步，否则停止

可视化如下：

3 基本问题

我们通常关注隐马尔可夫模型的三个基本问题：

1. 评估匹配程度：给定模型 $\lambda =(\mathit{A},\mathit{B},\mathit{\pi })$，如何计算观测序列 $\mathbf{x}=\{x_1,x_2,\dots ,x_n\}$ 的概率 $P(\mathbf{x}\mid \lambda )$.
2. 推断隐藏状态：给定模型 $\lambda =(\mathit{A},\mathit{B},\mathit{\pi })$ 和观测序列 $\mathbf{x}=\{x_1,x_2,\dots ,x_n\}$，计算最匹配的隐藏状态 $\mathbf{y}=\{y_1,y_2,\dots ,y_n\}$.
3. 训练模型参数：给定观测序列 $\mathbf{x}=\{x_1,x_2,\dots ,x_n\}$，训练模型参数 $\lambda =(\mathit{A},\mathit{B},\mathit{\pi })$ 使得 $P(\mathbf{x}\mid \lambda )$ 最大。

回到第一节模型实例的具体例子，这三个问题便是：

1. 我们知道每个桶内球的具体数量，桶的转移概率，初始桶的概率，要求：产生某种观测序列的概率。
2. 我们知道每个桶内球的具体数量，桶的转移概率，初始桶的概率，要求：某种观测序列对应的隐藏状态序列。
3. 我们知道一个观测序列，要求：每个桶内球的具体数量，桶的转移概率，初始桶的概率。

4 概率计算（问题一）

4.1 基本方法

首先，对于给定隐藏状态 $\mathbf{y}=\{y_1,y_2,\dots ,y_n\}$，我们容易求出它的出现概率：

$$P(\mathbf{y}\mid \lambda )={\pi }_{y_1}{a}_{y_1,y_2}{a}_{y_2,y_3}\cdots a_{y_{n-1},y_n}={\pi }_{y_1}\prod _{i=2}^n{a}_{y_{i-1},y_i}$$

对于给定隐藏状态 $\mathbf{y}=\{y_1,y_2,\dots ,y_n\}$，观测序列 $\mathbf{x}=\{x_1,x_2,\dots ,x_n\}$ 的出现概率是：

$$P(\mathbf{x}\mid \mathbf{y},\lambda )=b_{y_1}(x_1)b_{y_2}(x_2)\cdots b_{y_n}(x_n)=\prod _{i=1}^n{b}_{y_i}(x_i)$$

$\mathbf{y},\mathbf{x}$ 联合出现的概率是：

$$P(\mathbf{x},\mathbf{y}\mid \lambda )=P(\mathbf{x}\mid \mathbf{y},\lambda )P(\mathbf{y}\mid \lambda )={\pi }_{y_1}{b}_{y_1}(x_1)\prod _{i=2}^n{a}_{y_{i-1},y_i}{b}_{y_i}(x_i)$$

然后求边缘概率，即可得到结果：

$$P(\mathbf{x}\mid \lambda )=\sum _{\mathbf{y}}P(\mathbf{x},\mathbf{y}\mid \lambda )$$

接下来分析一下计算复杂度，对于长 $T$ 的序列，状态空间大小 $N$，一共有可能出现 $N^T$ 种隐藏状态序列 $\mathbf{y}=\{y_1,y_2,\dots ,y_n\}$. 对于每个隐藏状态序列，我们需要 $T$ 次计算。

因此计算复杂度为：$O(T{N}^T)$. 复杂度呈指数增长，对于较长序列几乎不可用。

4.2 前向算法

前向算法就是一种动态规划算法，通过动态规划算法，我们不再关心每一种状态序列具体的概率，而是关注每一步的概率。这样相当于将许多情况合并到一起，大幅减少了计算复杂度。

给定隐马尔可夫模型 $\lambda$，定义到时刻 $t$ 部分观测序列为 $x_1,x_2,\dots ,x_t$ 且状态 $y_t$ 为 $s_i$​ 的概率为前向概率，记为：

$${\alpha }_t(i)=P(x_1,x_2,\cdots ,x_t,y_t=s_i\mid \lambda )$$

状态转移方式：

$${\alpha }_{t+1}(i)=[\sum _{j=1}^N{\alpha }_t(j)a_{s_j,s_i}]b_{s_i}(x_{t+1})$$

对于每一步，我们需要计算 $i=1,2,\dots ,N$ 的前向概率。

当然，动态规划的初始值也非常重要。在本问题中初始值为 $t=1$ 的情况：

$${\alpha }_1(i)={\pi }_i{b}_{i,1}$$

当我们递推到序列结尾 $t=T$ 时，就可以开始计算结果了：

$$P(\mathbf{y}\mid \lambda )=\sum _{i=1}^N{\alpha }_T(i)$$

接下来分析一下计算复杂度，每次递推需要计算 $N^2$ 次，一共需要 $T{N}^2$ 次计算。该复杂度至少关于 $T$ 呈线性增长了，基本可以。

例题：

• $\mathcal{Y}=\{s_1,s_2,s_3\}$
• $\mathcal{X}=\{A,B\}$
• $\mathit{\pi }=(1,0,0)$
• $\mathit{A}=\left[\begin{array}{ccc}0.4& 0.6& 0\\ 0& 0.8& 0.2\\ 0& 0& 1\end{array}\right]$
• $\mathit{B}=\left[\begin{array}{cc}0.7& 0.3\\ 0.4& 0.6\\ 0.8& 0.2\end{array}\right]$

求观察序列 $ABAB$ 概率。

答案：

$$P(ABAB\mid \lambda )=\sum _{i=1}^N{\alpha }_4(i)=0.0717696$$

4.3 后向算法

后向算法实际上就是前向算法反着来求，前后向算法实际上是等价的。

给定隐马尔可夫模型 $\lambda$，定义时刻 $t$ 到 $T$ 部分观测序列为 $x_{t+1},\dots ,x_T$ 且状态 $y_t$ 为 $s_i$​ 的概率为后向概率，记为：

$${\beta }_t(i)=P(x_{t+1},x_{t+2},\cdots ,x_T\mid y_t=s_i,\lambda )$$

• 初始化：${\beta }_T(i)=1$
• 状态转移：${\beta }_t(i)=\sum _{j=1}^N{a}_{ij}{b}_j(y_{t+1}){\beta }_{t+1}(j)$
• 结果：$P(\mathbf{y}\mid \lambda )=\sum _{i=1}^N{\pi }_i{b}_i(y_1){\beta }_1(i)$

5 状态预测（问题二）

5.1 近似算法

近似算法就是朴素的贪心算法，即在每个时刻 $t$ 选取在该时刻最有可能出现的状态 $y_t^{\ast }$.

给定模型 $\lambda$ 和观测序列 $\mathbf{x}=\{x_1,x_2,\dots ,x_T\}$，在时刻 $t$ 时，系统处于状态 $s_i$ 的概率 ${\gamma }_t(i)$ 为：

$${\gamma }_t(i)=\frac{{\alpha }_t(i){\beta }_t(i)}{P(\mathbf{x}\mid \lambda )}=\frac{{\alpha }_t(i){\beta }_t(i)}{\sum _{j=1}^N{\alpha }_t(j){\beta }_t(j)}$$

那么，对于每一时刻选取最有可能出现的状态：

$$y_t^{\ast }=\arg \underset{1\le i\le N}{max}{\gamma }_t(i)$$

即可得到预测的状态序列：${\mathbf{y}}^{\ast }=\{y_1^{\ast },y_2^{\ast },\dots ,y_n^{\ast }\}$​

容易发现，因为该算法完全忽略了相邻状态的限制，该算法求到的序列有可能是实际中不可能存在的非法序列。

即可能会发生，对于相邻状态 $y_t^{\ast }=s_i$ 和 $y_{t+1}^{\ast }=s_j$，它们不可能进行转移 $a_{i,j}=0$.

5.2 维特比 (Viterbi) 算法

维特比算法是一种动态规划算法，它的核心思路是：如果最优路径在时刻 $t$ 通过状态 $y_t^{\ast }$，那么该路径从 $1\sim t$ 的部分一定是所有可能的路径中最优的部分。

定义在时刻 $t$ 时，状态为 $s_i$ 的所有状态路径 $(y_1,y_2,\cdots ,y_t)$ 中概率的最大值为：

$${\delta }_t(i)=\underset{y_1,y_2,\cdots ,y_t}{max}P(y_t=s_i,y_{t-1},y_{t-2},\cdots ,y_1,x_t,\cdots ,x_1\mid \lambda )$$

那么，变量 $\delta$ 的转移方式即为：

$${\delta }_{t+1}(i)=\underset{1\le j\le N}{max}[{\delta }_t(j)a_{s_j,s_i}]\cdot b_{s_i}(y_{t+1})$$

另外再记在时刻 $t$ 时，状态为 $s_i$ 的所有状态路径 $(y_1,y_2,\cdots ,y_t)$ 中概率的最大的路径的上一个节点（即 $t-1$ 时刻节点）为：

$${\psi }_t(i)=\arg \underset{1\le j\le N}{max}[{\delta }_{t-1}(j)a_{s_j,s_i}]$$

通俗来说 $\psi$ 这个变量就相当于动态规划里的 $\mathrm{prev}$ 指针，用来后期回溯用的。

那么接下来，维特比算法的步骤为：

• 初始化：${\delta }_1(i)={\pi }_i{b}_i(y_1),{\psi }_1(i)=0$.
• 递推：根据上文转移公式，通过 ${\delta }_{t-1}$ 计算出 ${\delta }_t$ 和 ${\psi }_t$.
• 结果：$P^{\ast }=\underset{1\le i\le N}{max}{\delta }_T(i),y_T^{\ast }=\arg \underset{1\le i\le N}{max}{\delta }_T(i)$​
• 反向回溯：$i_t^{\ast }={\psi }_{t+1}(i_{t+1}^{\ast })$

例题：

HMM 模型参数和上一个例题一致，区别是本题求的是最可能的状态序列 ${\mathbf{y}}^{\ast }=\{y_1^{\ast },y_2^{\ast },\dots ,y_n^{\ast }\}$.

答案：

• $P^{\ast }=\underset{1\le i\le 3}{max}{\delta }_4(i)=0.0387072$
• $y_4^{\ast }=\arg \underset{1\le i\le 3}{max}{\delta }_4(i)=2$
• ${\mathbf{y}}^{\ast }=\{1,2,2,2\}$

6 参数学习（问题三）

6.1 极大似然估计（有监督）

如果我们同时拥有观测序列和其对应的状态序列，那么就可以用监督学习的方法进行参数学习。

假设训练数据包含 $S$ 个长度相同的观测序列和对应的状态序列：$\{({\mathbf{x}}_1,{\mathbf{y}}_1),({\mathbf{x}}_2,{\mathbf{y}}_2),\dots ,({\mathbf{x}}_S,{\mathbf{y}}_S)\}$

估计 $\mathbf{A}$

设训练数据中，从状态 $i$ 转移到状态 $j$ 的频数为 $C_{ij}$，那么：

$${\hat{a}}_{ij}=\frac{C_{ij}}{\sum _{k=1}^N{C}_{ik}}$$

估计 $\mathbf{B}$

设训练数据中，状态为 $i$ 时观测为 $s_j$ 的频数为 $C_{ij}$，那么：

$${\hat{b}}_{ij}=\frac{C_{ij}}{\sum _{k=1}^M{C}_{ik}}$$

估计 $\mathit{\pi }$

设 $S$ 个训练数据中，初始状态为 $s_i$ 的频数为 $C_i$，那么：

$${\pi }_i=\frac{C_i}{S}$$

6.2 Baum-Welch 算法（无监督）

如果我们只拥有观测序列，那么就只能用无监督的方式学习。

本方法基于 EM 算法：https://io.zouht.com/113.html 具体推导省略

$$\begin{array}{rl}{a}_{ij}& =\frac{\sum _{t=1}^{T-1}P(\mathbf{x},y_t=s_i,y_{t+1}=s_j\mid \overline{\lambda })}{\sum _{t=1}^{T-1}P(\mathbf{x},y_t=s_i\mid \overline{\lambda })}\\ b_{jk}& =\frac{\sum _{t=1}^{T}P(\mathbf{x},y_t=s_j\mid \overline{\lambda })I(x_t=s_k)}{\sum _{t=1}^{T}P(\mathbf{x},y_t=s_j\mid \overline{\lambda })}\\ {\pi }_i& =\frac{P(\mathbf{x},y_1=s_i\mid \overline{\lambda })}{P(\mathbf{x}\mid \overline{\lambda })}\end{array}$$