残差神经网络 (Residual Neural Network, ResNet): 属于深度学习模型的一种，其核心在于让网络的每一层不直接学习预期输出，而是学习与输入之间的残差关系。

1 背景

由于梯度爆炸/梯度消失的问题，越深的深度学习模型越难收敛。通过归一化可以解决这个问题，让几十层的深度学习模型能够收敛。但是即使几十层的深度学习模型能够收敛，它的准确率反而不如浅层的模型，这个问题被称为“性能退化”问题。

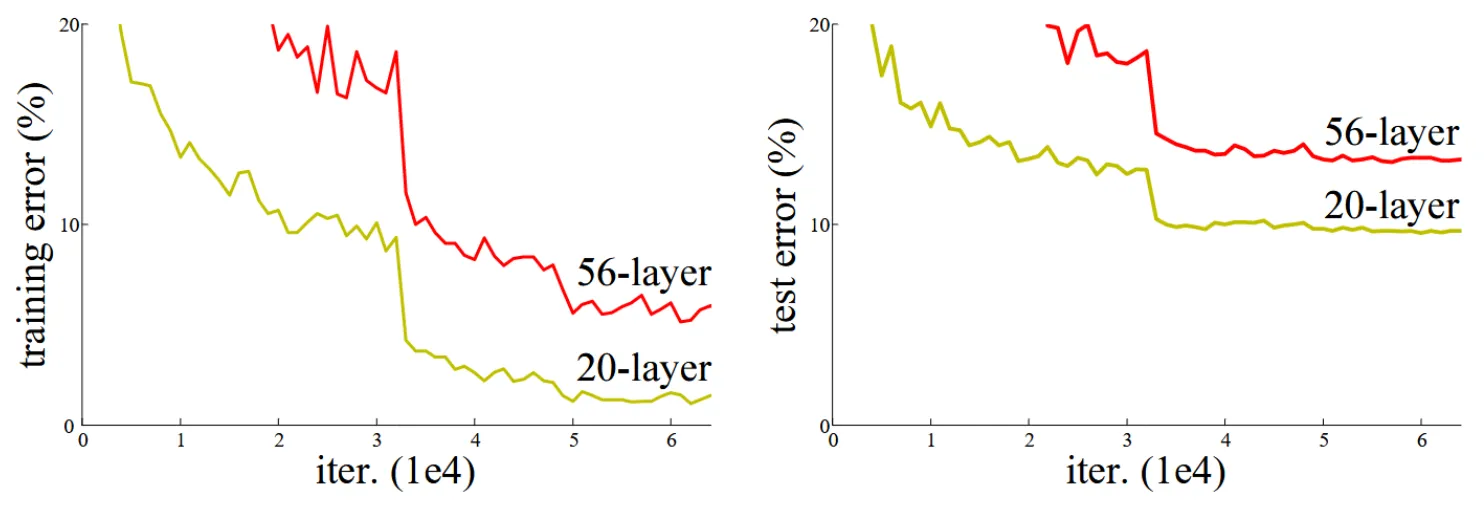
图片来源：https://arxiv.org/abs/1512.03385

理论上，通过添加网络层给一个模型加深不应该导致更高的训练误差，如果这些额外层被设置为特征映射，深层的模型至少能和浅层部分表现相同。但实际情况表明了，优化器并不能有效地将这些层的参数设定为特征映射。

特征映射 (Identity Mapping): 是指一个网络层或者模型结构中的一种操作，其作用是将输入直接传递到输出，不进行任何变换或者操作。换句话说，特征映射保持输入的信息不变，只是简单地将输入复制到输出。

2 残差网络

如果原始层希望拟合的映射为 $\mathcal{H}(\mathrm{x})$，在残差网络中，我们就改为拟合残差，即层输入和输出的差值：

$$ \mathcal{F}(\mathrm{x})=\mathcal{H}(\mathrm{x})-\mathrm{x} $$

那么原始的映射就可以写作：

$$ \mathcal{H}(\mathrm{x})=\mathcal{F}(\mathrm{x})+\mathrm{x} $$

上述式子可以理解为，在原始的网络上进行一个跳接，将层的输出和跳接的输入相加后再进行激活，如下图：

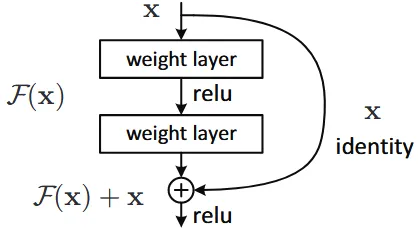
图片来源：https://arxiv.org/abs/1512.03385

设计以上这些结构，一个重要的原因是让优化器把残差层设置为特征映射比普通层更简单。因为只需将残差层置为 $0$​ 即代表了特征映射，而普通层还需要复杂调整来实现特征映射。因此，残差网络更有可能保证模型加深时的准确度。

3 前向传播

前向传播非常简单，就是上一节所说，添加一个跳接，将层的输出和跳接输入相加后再激活。但是有一个需要注意的点是，跳接并不是一定只能跳接两层，是可以跳接任意层数的（但注意，跳接一层是无意义的）.

综上，一个残差块可以记作：

$$ \mathrm{y}=\mathcal{F}(\mathrm{x})+\mathrm{x} $$

其中，$\mathrm{x}$ 和 $\mathrm{y}$ 就是残差块的输入和输出，$\mathcal{F}$ 代表了残差映射，它可以是多个层堆叠。例如跳接两层的话：

$$ \mathcal{F}=W_2\sigma(W_1\mathrm{x}) $$

需要注意的是，$\mathcal{F}$ 最外侧是没有激活函数的，这次激活被移到了与跳接值相加后再进行。

接下来，给残差块的定义公式加上层数角标，转换一下写法：

$$ \mathrm{x}_{k+1}=\mathcal{F}(\mathrm{x}_k)+\mathrm{x}_k $$

然后递归应用此公式，就可以推导出：

$$ \mathrm{x}_{K}=\mathrm{x}_{k}+\sum_{i=k}^{K-1}\mathcal{F}(\mathrm{x}_i) $$

由上式可以看出，无论 $k,K$ 两层间隔多少，都会有一个信号能直接从 $k$ 传到 $K$ 层。

4 反向传播

将误差 $E$ 对 $\mathrm{x}_k$ 进行求导：

$$ \begin{align} \frac{\partial E}{\partial \mathrm{x_k}}&=\frac{\partial E}{\partial \mathrm{x}_K}\frac{\partial \mathrm{x}_K}{\partial \mathrm{x}_k}\\ &=\frac{\partial E}{\partial \mathrm{x}_K}(1+\frac{\partial}{\partial \mathrm{x}_k}\sum_{i=k}^{K-1}\mathcal{F}(\mathrm{x}_i))\\ &=\frac{\partial E}{\partial \mathrm{x}_K}+\frac{\partial E}{\partial \mathrm{x}_K}\frac{\partial}{\partial \mathrm{x}_k}\sum_{i=k}^{K-1}\mathcal{F}(\mathrm{x}_i) \end{align} $$

通过上式也可以看出，残差网络能够解决梯度消失问题。浅层梯度 $\frac{\partial E}{\partial \mathrm{x_k}}$ 总会包含 $\frac{\partial E}{\partial \mathrm{x}_K}$，因此即使 $\mathcal{F}$ 的梯度很小，也能保证总体梯度不消失。