注意力机制 (Attention)：是人工神经网络中一种模仿认知注意力的技术。这种机制可以增强神经网络输入数据中某些部分的权重，同时减弱其他部分的权重，以此将网络的关注点聚焦于数据中最重要的一小部分。数据中哪些部分比其他部分更重要取决于上下文。

本篇文章为论文 Attention Is All You Need 的笔记，因此本文的注意力机制架构遵照原论文。

1 总览

首先，我们通过非常简略的数学方式来总览一下注意力机制的操作过程，感受一下总体框架后，下文再进行详细展开。

对于一段文字：

$$ \text{The quick brown fox jumps over a lazy dog.} $$

首先将其切分为 Token（假设按词切分）：

$$ \text{The| quick| brown| fox| jumps| over| a| lazy| dog.} $$

然后通过 Embedding 将单词转为 $d_{\text{model}}$ 维的词向量：

$$ \vec{\mathrm{E}_1},\vec{\mathrm{E}_2},\dots,\vec{\mathrm{E}_9} $$

然后给词向量乘上 Query 矩阵 $\boldsymbol{W}_Q$，生成每个单词的 $d_q$ 维的查询向量 $\vec{\mathrm{Q}_i}=\boldsymbol{W}_Q\vec{\mathrm{E}_i}$：

$$ \vec{\mathrm{Q}_1},\vec{\mathrm{Q}_2},\dots,\vec{\mathrm{Q}_9} $$

然后给词向量乘上 Key 矩阵 $\boldsymbol{W}_K$，生成每个单词的 $d_k$ 维的键向量 $\vec{\mathrm{K}_i}=\boldsymbol{W}_K\vec{\mathrm{E}_i}$：

$$ \vec{\mathrm{K}_1},\vec{\mathrm{K}_2},\dots,\vec{\mathrm{K}_9} $$

然后将查询向量和键向量一一做向量点积，得到一个实数，这些值组成一个新的矩阵：

$$ \begin{bmatrix} \vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_1}&\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_1}&\dots&\vec{\mathrm{Q}_9}\cdot\vec{\mathrm{K}_1}\\ \vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_2}&\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_2}&\dots&\vec{\mathrm{Q}_9}\cdot\vec{\mathrm{K}_2}\\ \vdots&\vdots&\ddots&\vdots\\ \vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_9}&\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_9}&\dots&\vec{\mathrm{Q}_9}\cdot\vec{\mathrm{K}_9} \end{bmatrix} $$

然后对这些值进行列 SoftMax 操作：

$$ \begin{bmatrix} \text{Softmax}(\vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_1}) & \text{Softmax}(\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_1}) & \dots & \text{Softmax}(\vec{\mathrm{Q}_9}\cdot\vec{\mathrm{K}_1}) \\ \text{Softmax}(\vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_2}) & \text{Softmax}(\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_2}) & \dots & \text{Softmax}(\vec{\mathrm{Q}_9}\cdot\vec{\mathrm{K}_2}) \\ \vdots & \vdots & \ddots & \vdots \\ \text{Softmax}(\vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_9}) & \text{Softmax}(\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_9}) & \dots & \text{Softmax}(\vec{\mathrm{Q}_9}\cdot\vec{\mathrm{K}_9}) \end{bmatrix} $$

然后给每一项乘上 Value 矩阵 $\boldsymbol{W}_V$：

$$ M=\begin{bmatrix} \text{Softmax}(\vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_1}) \cdot \boldsymbol{W}_V & \text{Softmax}(\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_1}) \cdot \boldsymbol{W}_V & \dots & \text{Softmax}(\vec{\mathrm{Q}_9}\cdot\vec{\mathrm{K}_1}) \cdot \boldsymbol{W}_V \\ \text{Softmax}(\vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_2}) \cdot \boldsymbol{W}_V & \text{Softmax}(\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_2}) \cdot \boldsymbol{W}_V & \dots & \text{Softmax}(\vec{\mathrm{Q}_9}\cdot\vec{\mathrm{K}_2}) \cdot \boldsymbol{W}_V \\ \vdots & \vdots & \ddots & \vdots \\ \text{Softmax}(\vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_9}) \cdot \boldsymbol{W}_V & \text{Softmax}(\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_9}) \cdot \boldsymbol{W}_V & \dots & \text{Softmax}(\vec{\mathrm{Q}_9}\cdot\vec{\mathrm{K}_9}) \cdot \boldsymbol{W}_V \end{bmatrix} $$

然后计算每列的更新值 $\Delta\vec{\mathrm{E}_i}$：

$$ \Delta\vec{\mathrm{E}_i}=\sum_{k=1}^{n}M_{ki}\vec{\mathrm{E}_k} $$

原始 $\vec{\mathrm{E}_i}$ 经过注意力机制获取更多信息后，便可以更新为 $\vec{\mathrm{E}_i}'$：

$$ \vec{\mathrm{E}_i}'=\vec{\mathrm{E}_i}+\Delta\vec{\mathrm{E}_i} $$

上述过程的结构可以以下图方式展现：

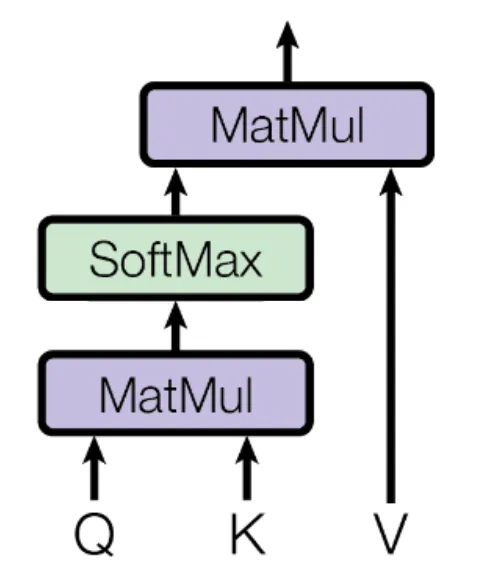
2 Query 查询

从 Token 嵌入得来的词向量是没有上下文语意信息的，例如 Transformer 到底指变形金刚、变压器还是一种机器学习模型，词向量中是没有相关信息的。为了获取这个 Token 具体的含义，就得从上下文 Token 中获取具体的信息。同时，有些上下文与该 Token 关联不大，比如 The，但有些词语对该 Token 关联非常大，例如 Model. 注意力机制便是让模型自己学会上下文之间的关联程度。

获取上下文关联程度的第一步是是求得查询向量，可以将查询向量理解为该 Token 对上下文提出的“问题”，接下来根据上下文 Token 的”回应“来确认他们之间的关联程度。

对于每个 Token 的词向量 $\vec{\mathrm{E}_i}$，让它与矩阵 $\boldsymbol{W}_Q$ 相乘获得对应的查询向量 $\vec{\mathrm{Q}_i}=\boldsymbol{W}_Q\vec{\mathrm{E}_i}$.

其中，$\vec{\mathrm{E}_i}$ 的维度为 $d_{\text{model}}$，$\vec{\mathrm{Q}_i}$ 的维度为 $d_Q$，那么显然 $\boldsymbol{W}_Q$ 就是一个 $d_q\times d_{\text{model}}$ 的矩阵。需要注意，这个矩阵是学习得来的参数，因此 Query 操作的参数量就是 $d_q\times d_{\text{model}}$.

3 Key 键

Key 向量便是对 Token 提出”问题“的”回应“。

对于每个 Token 的词向量 $\vec{\mathrm{E}_i}$，让它与矩阵 $\boldsymbol{W}_K$ 相乘获得对应的查询向量 $\vec{\mathrm{K}_i}=\boldsymbol{W}_K\vec{\mathrm{E}_i}$.

其中，$\vec{\mathrm{E}_i}$ 的维度为 $d_{\text{model}}$，$\vec{\mathrm{K}_i}$ 的维度为 $d_k$，原论文中 $d_k=d_q$，那么显然 $\boldsymbol{W}_K$ 就是一个 $d_q\times d_{\text{model}}$ 的矩阵。需要注意，这个矩阵是学习得来的参数，因此 Key 操作的参数量也是 $d_q\times d_{\text{model}}$.

获得了 Key 值后，就要通过 Compatibility Function (评分函数) 来获得关联程度了。评分函数可以是向量点积：

$$ \text{Compatibility Function}(\vec{\mathrm{Q}_i},\vec{\mathrm{K}_i})=\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_i} $$

上面我们说到原论文中 $d_k=d_q$，那么如果 $d_k\neq d_q$，那么显然不能靠向量点积的评分函数了，而是需要加性评分函数。加性评分函数使用一个前馈神经网络来计算 Query 向量和 Key 向量的关联程度，这个神经网络只有一个隐藏层。

计算得到关联程度形成矩阵：

$$ \begin{bmatrix} \vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_1}&\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_1}&\dots&\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_1}\\ \vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_2}&\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_2}&\dots&\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_2}\\ \vdots&\vdots&\ddots&\vdots\\ \vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_i}&\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_i}&\dots&\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_i} \end{bmatrix} $$

接下来有一个可选步骤——Mask (掩码)。对于大语言模型，训练时是通过上文来生成下文，因此上文是不可以从下文获取信息的，否则这就泄露了要预测的信息，造成干扰。但对于文本翻译，就不存在这种问题，因此掩码就是不必要的。

为了防止上文获取下文信息，可以直接将这些关联程度项设为 $-\infty$，这一步就叫掩码：

$$ \begin{bmatrix} \vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_1}&\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_1}&\dots&\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_1}\\ -\infty&\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_2}&\dots&\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_2}\\ \vdots&\vdots&\ddots&\vdots\\ -\infty&-\infty&\dots&\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_i} \end{bmatrix} $$

还需要注意的一点是，经过点积评分函数后会扩大原数据的方差，导致 Softmax 过于关注小梯度：若 $q,k$ 为独立的随机变量，那么它的均值为 $0$ 方差为 $1$，但是 $q\cdot k$ 的均值为 $0$，方差为 $d_k$. 为了抵消这个问题，给每一项缩小 $\sqrt{d_k}$：

$$ \begin{bmatrix} \frac{\vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_1}}{\sqrt{d_k}} & \frac{\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_1}}{\sqrt{d_k}} & \dots & \frac{\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_1}}{\sqrt{d_k}} \\ -\infty & \frac{\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_2}}{\sqrt{d_k}} & \dots & \frac{\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_2}}{\sqrt{d_k}} \\ \vdots & \vdots & \ddots & \vdots \\ -\infty & -\infty & \dots & \frac{\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_i}}{\sqrt{d_k}} \end{bmatrix} $$

再进行列 SoftMax，这些被置为 $-\infty$ 的项就变成 $0$ 了：

$$ M=\begin{bmatrix} \text{Softmax}\left(\frac{\vec{\mathrm{Q}_1}\cdot\vec{\mathrm{K}_1}}{\sqrt{d_k}}\right) & \text{Softmax}\left(\frac{\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_1}}{\sqrt{d_k}}\right) & \dots & \text{Softmax}\left(\frac{\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_1}}{\sqrt{d_k}}\right) \\ & \text{Softmax}\left(\frac{\vec{\mathrm{Q}_2}\cdot\vec{\mathrm{K}_2}}{\sqrt{d_k}}\right) & \dots & \text{Softmax}\left(\frac{\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_2}}{\sqrt{d_k}}\right) \\ & & \ddots & \vdots \\ 0 & & & \text{Softmax}\left(\frac{\vec{\mathrm{Q}_i}\cdot\vec{\mathrm{K}_i}}{\sqrt{d_k}}\right) \end{bmatrix} $$

4 Value 值

计算了关联程度，下一步就是与 Value 矩阵相乘获得最终的更新，记上述矩阵 $p$ 行 $q$ 列元素为 $M_{pq}$，那么：

$$ \Delta\vec{\mathrm{E}_i}=\sum_{k=1}^{n}M_{ki}\boldsymbol{W}_V\vec{\mathrm{E}_k} $$

其中，$\Delta\vec{\mathrm{E}_i}$ 的维度为 $d_{\text{model}}$，$\vec{\mathrm{E}_i}$ 的维度为 $d_{\text{model}}$，那么显然 $\boldsymbol{W}_V$ 就是一个 $d_{\text{model}}\times d_{\text{model}}$ 的方阵。需要注意，这个矩阵是学习得来的参数，因此 Value 操作的参数量也是 $d_{\text{model}}\times d_{\text{model}}$​.

综上，注意力头总参数量为：$d_{\text{model}}(2d_q+d_{\text{model}})$

上述过程的结构可以以下图方式展现：

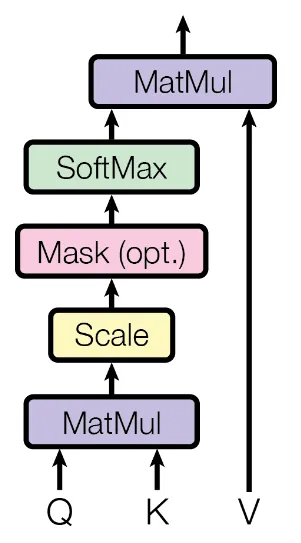
用公式来表示就是：

$$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$

5 多头注意力

实际情况中，$d_{\text{model}}$ 往往非常大，可以达到 $10^4$ 数量级，这就导致 $\boldsymbol{W}_V$ 这个 $d_{\text{model}}\times d_{\text{model}}$ 的方阵参数量非常大，占据了模型的大部分参数。

多头注意力的思想就是，与其用一个完整维度的大参数单头注意力，不如将其拆分为多个低维度的小参数注意力，称为多头注意力。这样的效果要好于单头注意力。

我们可以用低秩分解的思想，将 $\boldsymbol{W}_V$ 拆分为 $d_{\text{model}}\times d_v$ 和 $d_v\times d_{\text{model}}$ 的两个矩阵：$\boldsymbol{W}_{V\uparrow}$ 和 $\boldsymbol{W}_{V\downarrow}$. 那么，原来的 Value 计算步骤就变成了：

$$ \Delta\vec{\mathrm{E}_i}=\sum_{k=1}^{n}M_{ki}\boldsymbol{W}_{V\uparrow}\boldsymbol{W}_{V\downarrow}\vec{\mathrm{E}_k} $$

低秩拆分是一种有损压缩技术，可以在一定程度上保留数据的重要特征，但无法完全保留原始数据的所有信息。另外，我们也可以将这个操作理解为做了两次线性映射：先将 $\vec{\mathrm{E}_i}$ 从 $d_{\text{model}}$ 维空间线性映射到低维的 $d_v$ 空间，再从低维的 $d_v$ 空间重新线性映射回 $d_{\text{model}}$ 维空间（原论文中，拆分后的 $\boldsymbol{W}_{V\uparrow}$ 和 $\boldsymbol{W}_{V\downarrow}$ 就直接被记为 Linear 了）.

矩阵乘法可以看作线性映射，例如有一个 $n$ 维向量 $\vec{p}$，将它与 $m\times n$ 的矩阵 $\boldsymbol{M}$ 相乘可以得到一个 $m$ 维向量 $\vec{q}$：

$$ \boldsymbol{M}_{m\times n}\vec{p}_{n\times1}=\vec{q}_{m\times1} $$

这个矩阵 $\boldsymbol{M}$ 就实现了将 $n$ 维空间的向量 $\vec{p}$ 映射到 $m$ 维空间里，变成向量 $\vec{q}$​.

上述拆分后仍然是单头注意力，接下来就是叠加注意力头了。最简单想到的一种方式是，直接将单头注意力复制 $h$ 份，每个注意力头有独立的参数（如第 $i$ 个注意力头的参数 $\boldsymbol{W}^{Q}_i,\boldsymbol{W}^{K}_i,\boldsymbol{W}^{V\downarrow}_i,\boldsymbol{W}^{V\uparrow}_i$），最后将 $h$ 个注意力头的结果取平均。

但是原论文并没有用这个方式。在原论文中，将单头注意力复制 $h$ 份后，$\boldsymbol{W}_{V\uparrow}$ 并不是独立的参数，具体来说：

1. 每个注意力头拥有独立的参数 $\boldsymbol{W}^{Q}_i,\boldsymbol{W}^{K}_i,\boldsymbol{W}^{V\downarrow}_i$
2. 每个注意力头求得 $\overrightarrow{\text{head}}_i=\sum_{k=1}^{n}M_{ki}\boldsymbol{W}_{V\downarrow}\vec{\mathrm{E}_i}$，显然这个 $\vec{\text{head}}_i$ 是 $d_v$ 维的向量。
3. 将 $h$ 个注意力头得到的结果向量拼接得到 $\overrightarrow{\text{MultiHead}}=\mathrm{Concat}(\overrightarrow{\text{head}}_1,\overrightarrow{\text{head}}_2,\dots,\overrightarrow{\text{head}}_N)$，显然这个 $\overrightarrow{\text{MultiHead}}$ 是 $h\times d_v$ 维的向量。
4. 然后将 $\overrightarrow{\text{MultiHead}}$ 用 $\boldsymbol{W}_{V\uparrow}$ 重新映射回 $d_{\text{model}}$ 维的空间，显然此时 $\boldsymbol{W}_{V\uparrow}$ 应当是 $d_{\text{model}}\times hd_v$ 的矩阵。

综上，对于 $h$ 个注意力头的多头注意力，参数量为：

$$ hd_{\text{model}}(d_q+d_k+d_v)+hd_{\text{model}}d_v=hd_{\text{model}}(d_q+d_k+2d_v) $$

对于原论文，$d_q=d_k=d_v$，那么参数量为：$4hd_{\text{model}}d_q$​

上述过程的结构可以以下图方式展现：

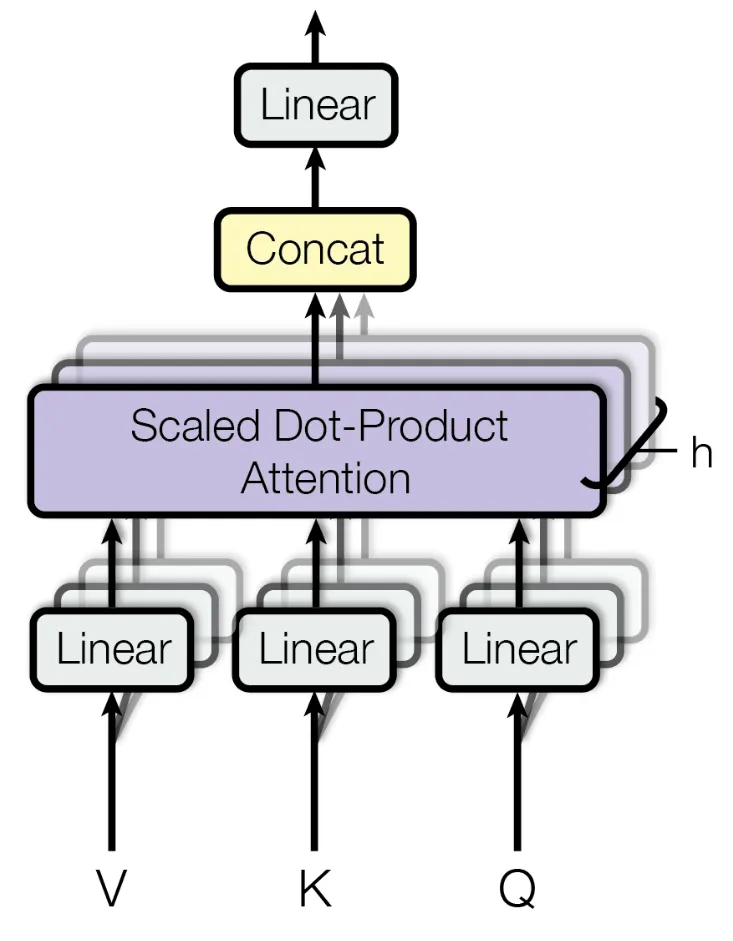
需要注意的是，上面原论文的图将 $\boldsymbol{W}_{V\downarrow}$ 表示为 Linear。虽说看着不一样，实际上是完全一样的，只是符号的区别。