链式前向星：一种静态链表存储，用边集数组和邻接表相结合，可以快速访问一个顶点的所有邻接点

链式前向星

数据储存

constexpr int MAXN = 1e5 + 10;
int h[MAXN], e[MAXN], ne[MAXN], idx;
// h   - 头节点
// e   - 邻接节点
// ne  - 链表指针
// idx - 当前用到的下标

存图

下标从 $0$ 开始：

（这种一定需要 memset(h, -1, sizeof(h)); 初始化）

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx++;
}

下标从 $1$ 开始：

（这种如果是多测也别忘记 memset(h, 0, sizeof(h)); 初始化）

void add(int a, int b)
{
    idx++;
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
}

遍历

下标从 $0$ 开始：

（~i 其实也是一样的）

for (int i = h[x]; i != -1; i = ne[i])
{
    int &cur = e[i];
    // do something...
}

下标从 $1$ 开始：

for (int i = h[x]; i; i = ne[i])
{
    int &cur = e[i];
    // do something...
}

旧版文章内容

时间复杂度：$O(\left|E\right|+\left|V\right|)$

此为遍历全图的复杂度。$\left|E\right|$ 为边数，$\left|V\right|$ 为顶点数。

代码实现：

#include <bits/stdc++.h>
#define SIZE 1000

using namespace std;

struct EDGE
{
    int to, weight, next;
} edge[SIZE];
int head[SIZE];

int V, E; // E边数，V顶点数
int cnt;  // 储存边时的下标

void init()
{
    cnt = 0;
    // 全部初始化为-1
    for (int i = 1; i <= V; i++)
        head[i] = -1;
};

void add_edge(int start, int end, int weight)
{
    edge[cnt].to = end;           // 终点
    edge[cnt].weight = weight;    // 长度
    edge[cnt].next = head[start]; // 下一条边
    head[start] = cnt++;
}

void print()
{
    for (int i = 1; i <= V; ++i)
        for (int j = head[i]; j != -1; j = edge[j].next)
            cout << "Start = " << i << ", End = " << edge[j].to << ", Weight = " << edge[j].weight << endl;
}

int main()
{
    cin >> V >> E;
    init();
    // 输入边
    for (int i = 0; i < E; i++)
    {
        int a, b, w;
        cin >> a >> b >> w;
        add_edge(a, b, w);
    }
    // 遍历全图
    print();
    return 0;
};

数据结构分析：

该数据结构可以看作用链表来储存以第 $n$ 个点为起点的边，struct EDGE 中的 next 便是指向下一个元素的“指针”，head[ ] 下标为 $n$ 的那位储存着第 $n$ 个点的链表的头指针。

整个建图过程类似于链表的头插法：将新元素指向原链表的第一个元素，然后把头指针改为指向新元素。

下面用一个具体例子演示：

输入：
6 9
1 3 1
1 2 2
1 5 6
2 5 3
2 4 5
3 5 4
5 4 1
5 6 2
4 6 3

该图画出来的样子：

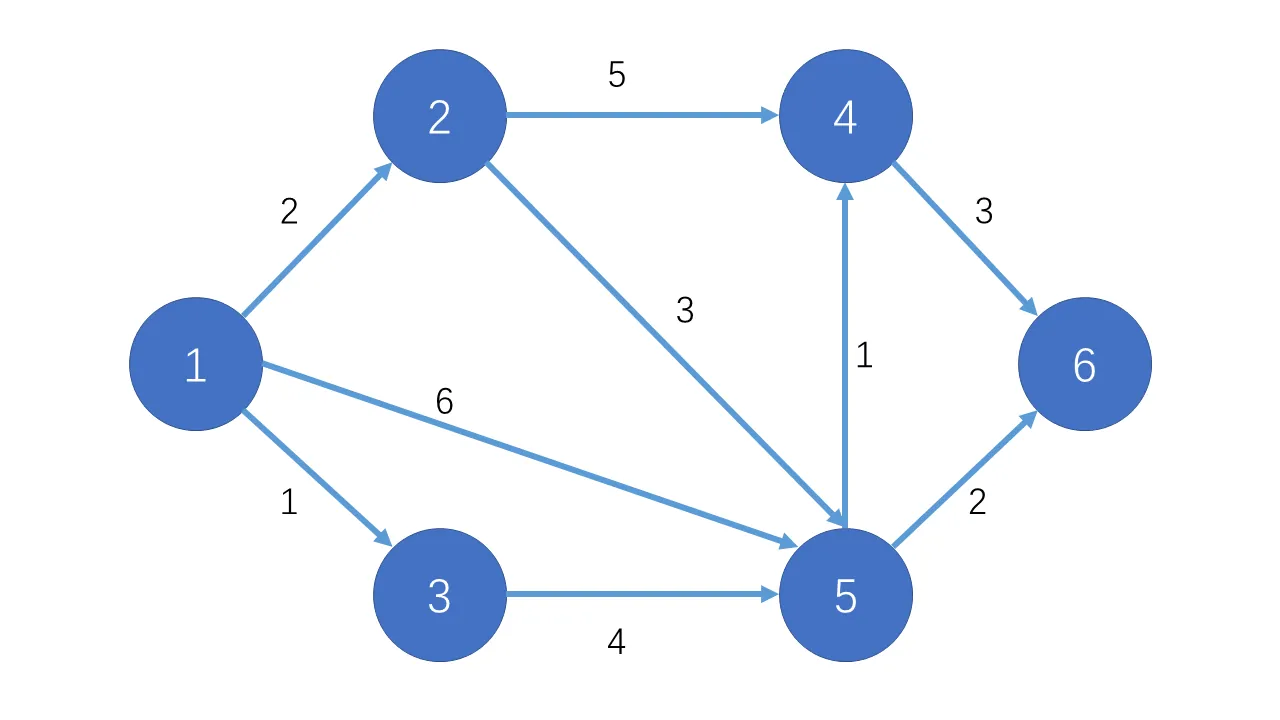
建图过程：

初始化：

声明数组 edge[E]、head[V+1]，E 为边数，V 为顶点数。本示例 E = 9, V = 6。
注意：如果为无向图，需要初始化双倍 edge[] 用于储存一条边的两个方向
将 head[1] ~ head[V] 初始化为 -1，代表链表结尾。（head[0] 这一位不使用）

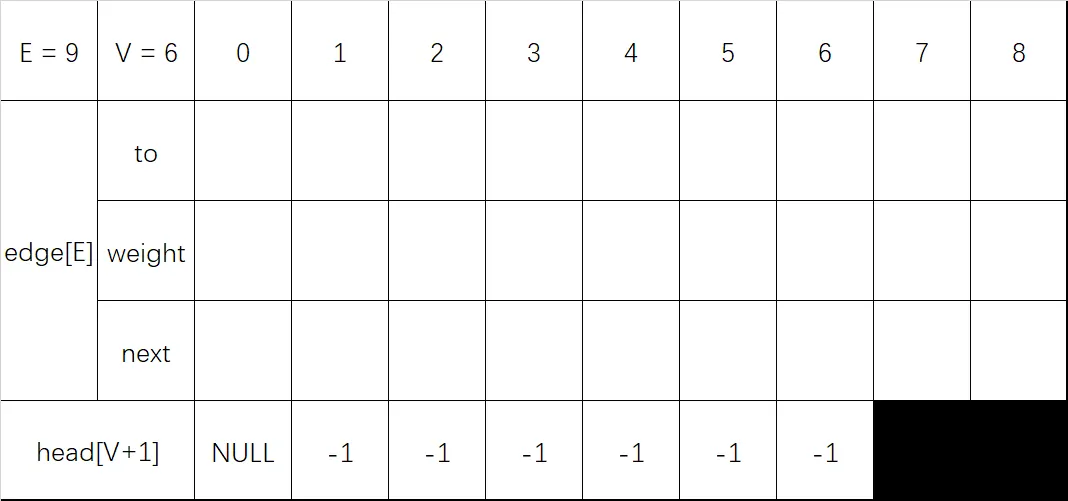
输入 1 3 1：

终点 to 设置为 3
长度 weight 设置为 1
next 设置为头指针 head[1] 的值 -1
更新头指针 head[1] 的值为当前节点 0（链表的头插法）

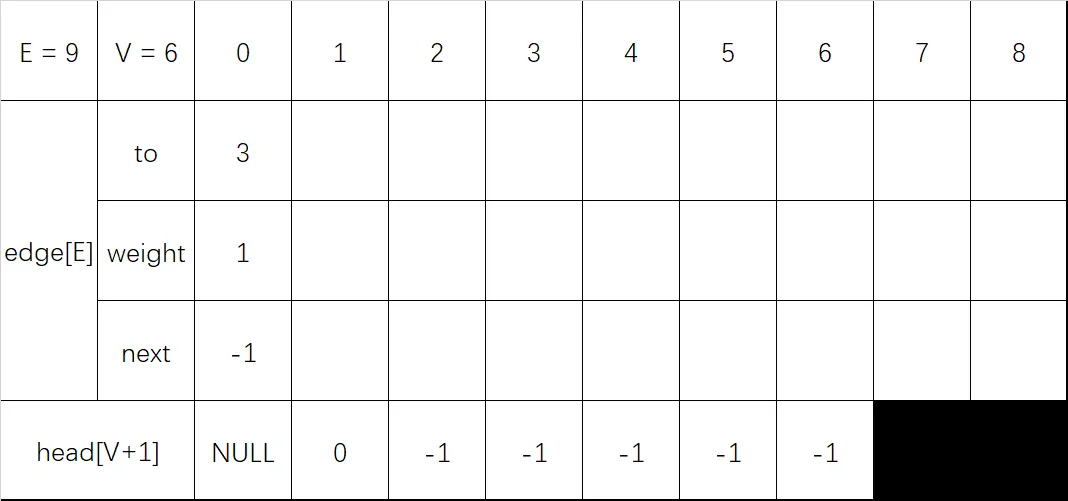
输入 1 2 2：

终点 to 设置为 2
长度 weight 设置为 2
next 设置为头指针 head[1] 的值 0
更新头指针 head[1] 的值为当前节点 1

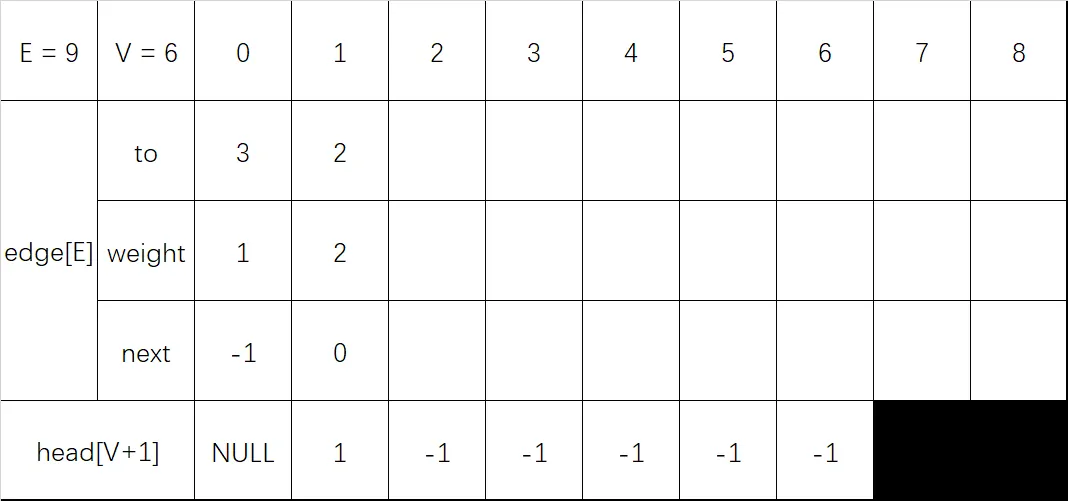
输入 1 5 6：

终点 to 设置为 5
长度 weight 设置为 6
next 设置为头指针 head[1] 的值 1
更新头指针 head[1] 的值为当前节点 2

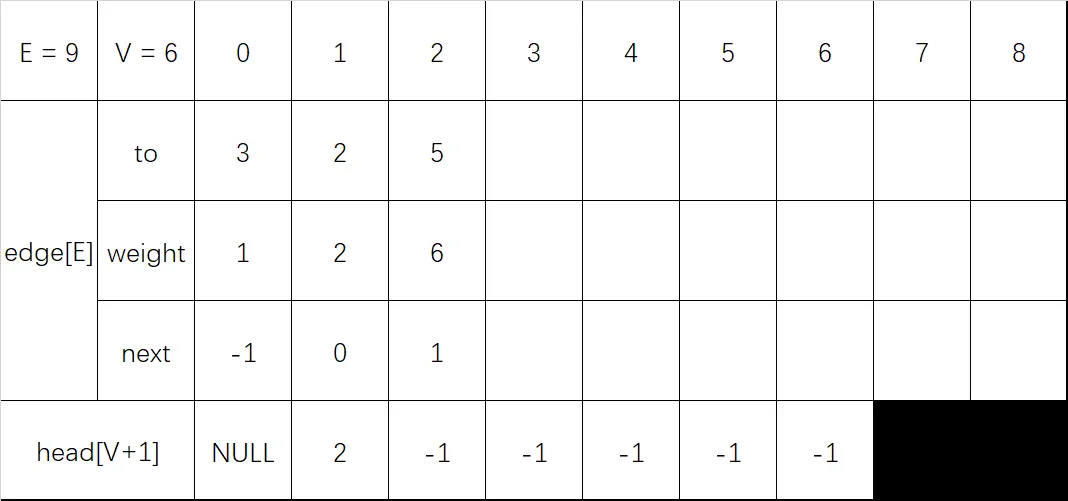
输入 2 5 3：

终点 to 设置为 5
长度 weight 设置为 3
next 设置为头指针 head[2] 的值 -1
更新头指针 head[2] 的值为当前节点 3

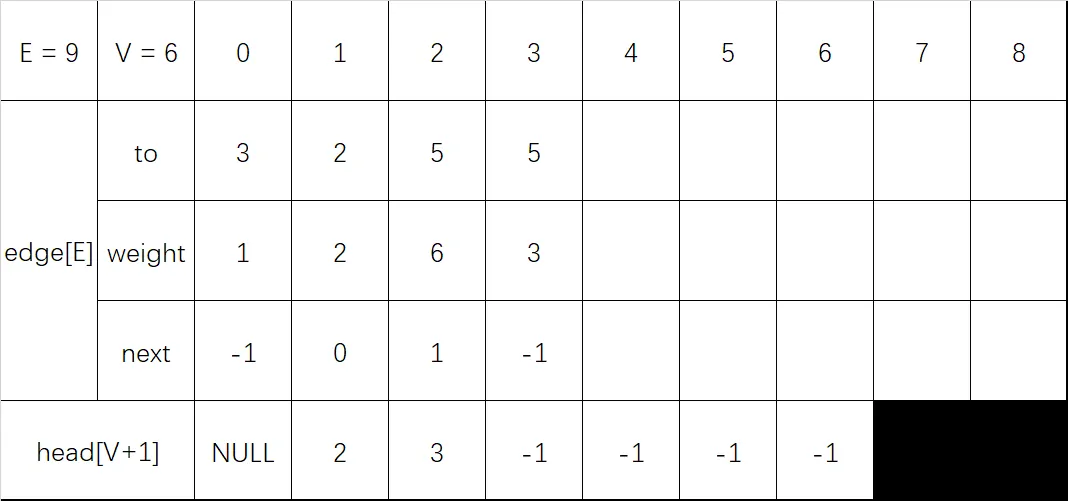
输入 2 4 5：

终点 to 设置为 4
长度 weight 设置为 5
next 设置为头指针 head[2] 的值 3
更新头指针 head[2] 的值为当前节点 4

输入 3 5 4：

终点 to 设置为 5
长度 weight 设置为 4
next 设置为头指针 head[3] 的值 -1
更新头指针 head[3] 的值为当前节点 5

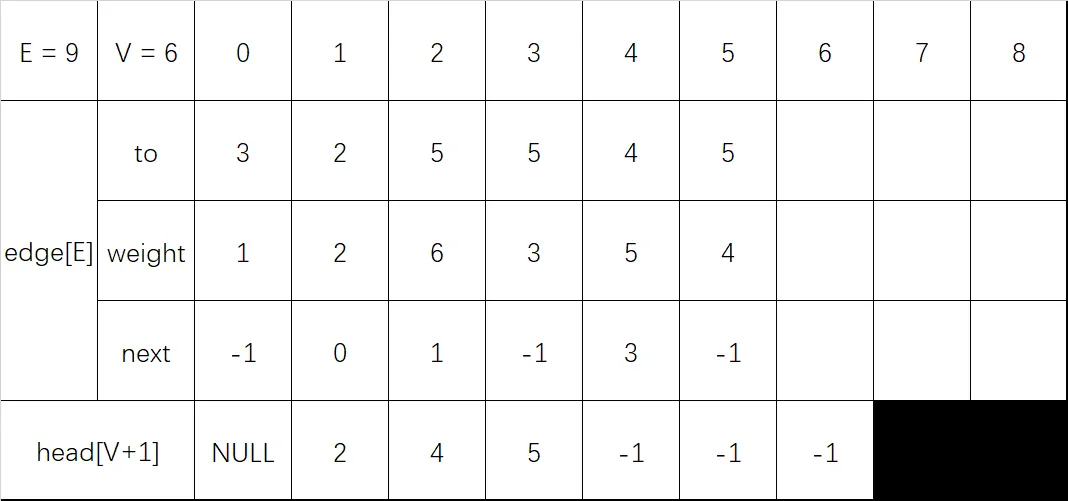
输入 5 4 1：(之后的过程略)

输入 5 6 2：

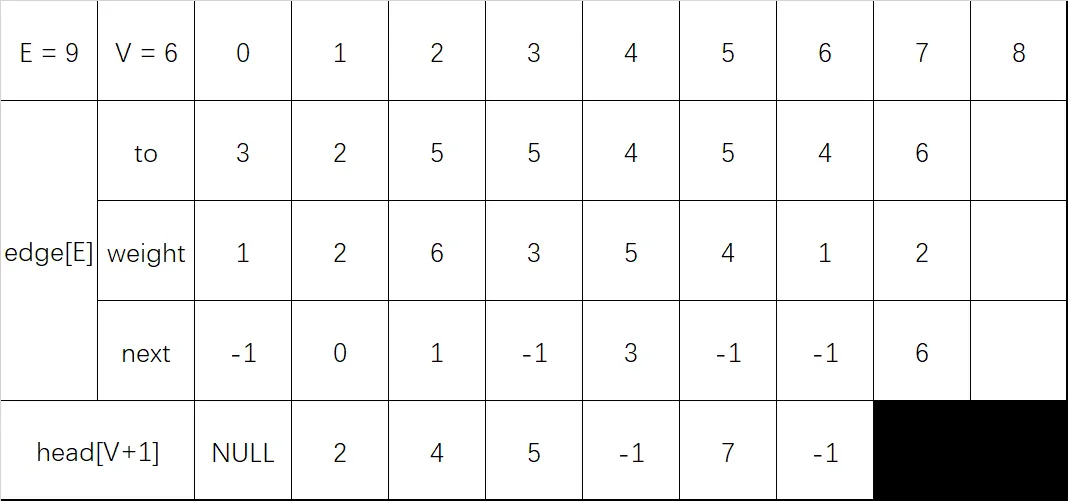
输入 4 6 3：

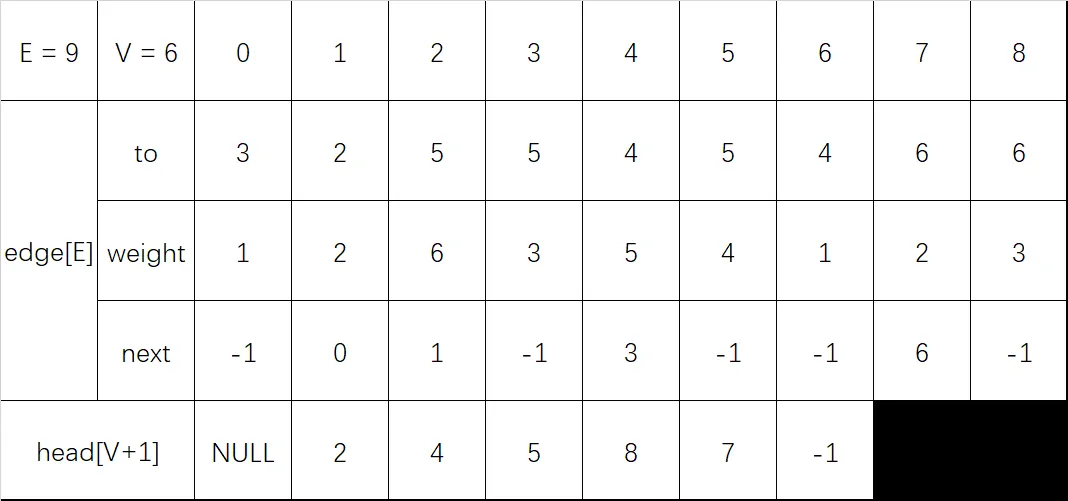
遍历过程：

// i为要遍历的点
for (int j = head[i]; j != -1; j = edge[j].next)
    cout << "Start = " << i << ", End = " << edge[j].to << ", Weight = " << edge[j].weight << endl;

例如要遍历以第 $1$ 个点为起点的所有边，那么首先找头指针 head[1] = 2，然后输出 edge[2]，其中 edge[2].next = 1，输出 edge[1]，其中 edge[1].next = 0，输出 edge[0]，其中 edge[0].next = -1，标志着已到链表结尾，遍历完成。

如果要遍历所有边，就写个 i 的从 1 到 V 的循环即可。

数据结构 | 链式前向星