求最小生成树（适合稠密图）：Prim (普林姆) 算法

Prim 算法

朴素版本

复杂度

时间复杂度：$O(\left|V\right|^2)$

$\left|V\right|$ 为顶点数，该版本适合稠密图，即 $\left|E\right|接近\left|V\right|^2$ 的图。

分析

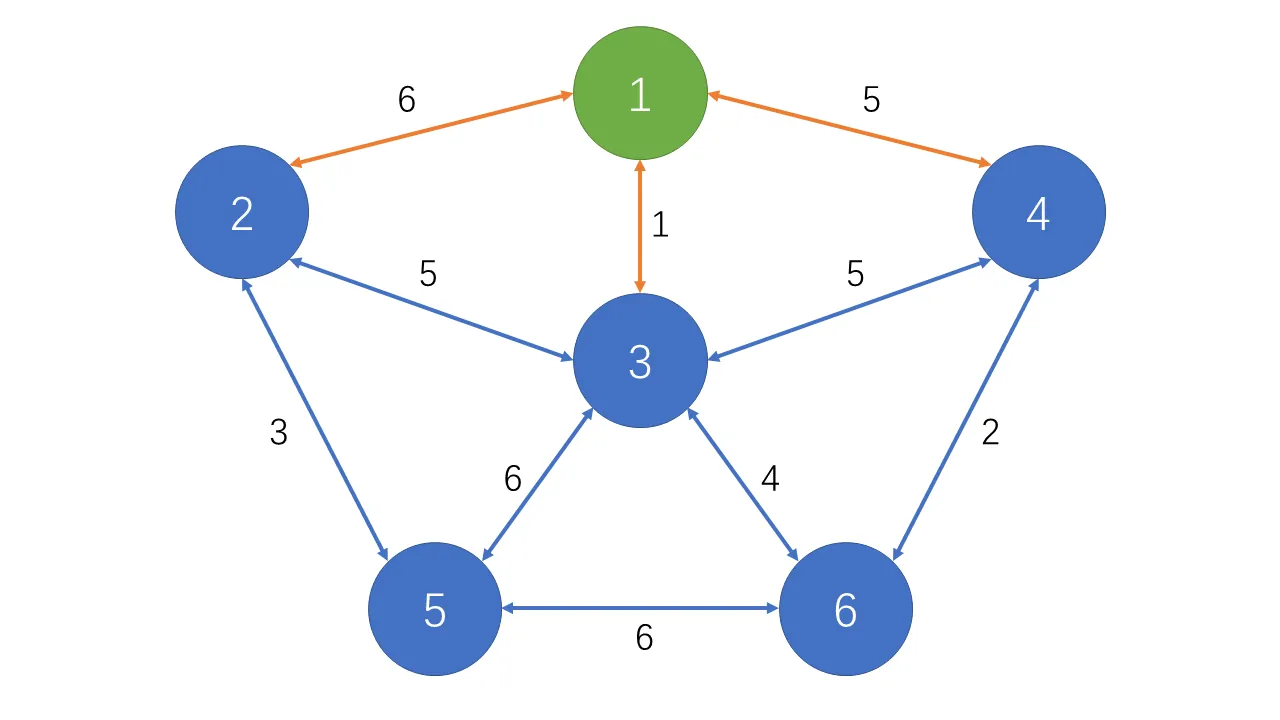
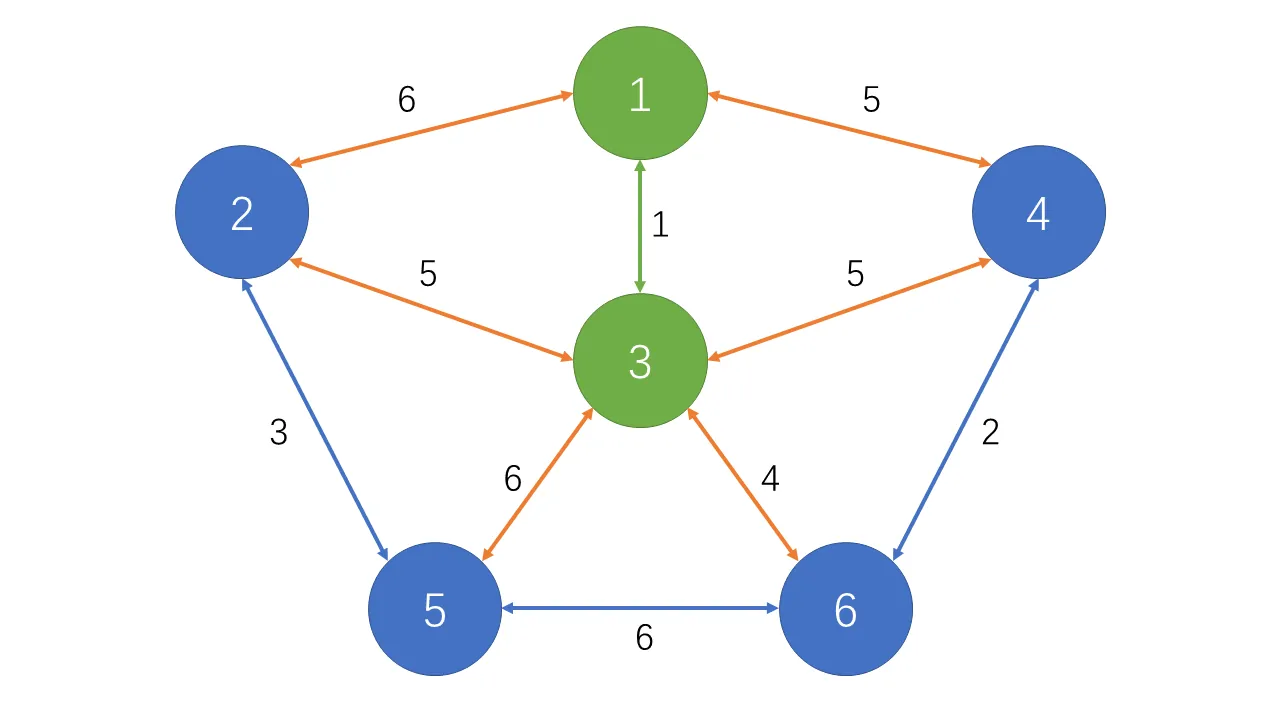
该算法的核心思路是，在能到达的边中选择最短的不会成环的边。如左图，我们从 $1$ 号点开始（可任选起点），目前 $1$ 号点的最短的边是 $1\leftrightarrow3$，因此选择该边。选择后可到达的边增多了，然后再在这些边中找到最短的边是 $3\leftrightarrow6$，则选择该边。后面不断进行该操作直到选择了 $\left|V\right|-1$ 条边。

上述思路与 Dijkstra 算法有相似之处，每次迭代均是选择最短的边。因此我们模仿 Dijkestra 的结构实现该算法，伪代码如下：

prim (G, dist[])
    初始化: dist[1~v]=+INF, dist[1]=0, ans=0
    for (循环v次)
        t=未选择的点的集合中dist[t]最小的顶点
        if (t为无穷大)
            return 图不连通
        ans加上dist[t]
        记t已选择
        for (j : 从t出发能到达的顶点的集合)
            if (若t到j的距离小于j到已选择点的距离)
                更新dist[j];
    return ans

注意，该算法中 dist 的含义不再是 Dijkstra 中到起点的距离，而是到已选择的点的最短距离，更新 dist[j] 时也直接使用边长即可。

代码实现

下面的代码和 Dijkstra 朴素版非常类似，大家可以对照查看，感受两个算法的异同。

const int MAXN = 510, INF = 0x3f3f3f3f; // INF代表无穷大
int g[MAXN][MAXN]; // 邻接矩阵存图
int dist[MAXN];    // 距离已选择点的最短距离
int vis[MAXN];     // 点是否选择
int v, e;          // v顶点数 e边数

int prim()
{
    int ans = 0;
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    for (int i = 0; i < v; i++)
    {
        int t = -1;
        for (int j = 1; j <= v; j++)
            if (!vis[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        if (dist[t] == INF)
            return INF;
        ans += dist[t];
        vis[t] = true;
        for (int j = 1; j <= v; j++)
            dist[j] = min(dist[j], g[t][j]);
    }
    return ans;
}

堆优化版本

复杂度

时间复杂度：$O((\left|E\right|+\left|V\right|)\log\left|V\right|)$

$\left|E\right|$ 为边数，$\left|V\right|$ 为顶点数，该版本适合稀疏图，即 $\left|E\right|\ll\left|V\right|^2$ 的图。

分析

朴素版本中，每次迭代都有一个查找最短边的过程，并且对所有点进行了更新操作，共需要 $2\left|V\right|$ 次循环。

针对查找最短边这一操作，二叉堆是一个很好的数据结构。我们建立一个小顶堆，即可在 $O(1)$ 时间内取得最小值。

针对更新操作，我们将存图方式改为邻接表，所以我们就可以只更新与该点相连的顶点，效率更高。

代码实现

下面的代码和 Dijkstra 堆优化版本非常类似，大家可以对照查看，感受两个算法的异同。

typedef pair<int, int> PII;
const int MAXN = 100010, INF = 0x3f3f3f3f;           // INF代表无穷大
int E, V;                                            // E边数 V顶点数
vector<PII> edge[MAXN];                              // 储存边，二元组为(权值,终点)
priority_queue<PII, vector<PII>, greater<PII>> pque; // 短的边在堆顶
int dist[MAXN];                                      // 储存节点到已选择点的最短距离
bool vis[MAXN];                                      // 是否已选择该点

int prim()
{
    int ans = 0, cnt = 0;
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    pque.push({dist[1], 1});
    while (!pque.empty())
    {
        PII cur = pque.top();
        pque.pop();
        if (vis[cur.second])
            continue;
        ans += cur.first;
        cnt++;
        vis[cur.second] = true;
        for (auto next : edge[cur.second])
        {
            if (dist[next.second] > next.first)
            {
                dist[next.second] = next.first;
                if (!vis[next.second])
                    pque.push({dist[next.second], next.second});
            }
        }
    }
    return cnt == V ? ans : INF;
}