题目 | typewriter - 颢天笔记

AtCoder Beginner Contest 246

F - typewriter

https://atcoder.jp/contests/abc246/tasks/abc246_f

Time Limit: 2 sec / Memory Limit: 1024 MB

Score : $500$ points

Problem Statement

We have a typewriter with $N$ rows. The keys in the ii-th row from the top can type the characters in a string $S_i$.

Let us use this keyboard to enter a string, as follows.

First, choose an integer $1 \le k \le N$.
Then, start with an empty string and only use the keys in the $k$-th row from the top to enter a string of length exactly $L$.

How many strings of length $L$ can be entered in this way? Since the answer can be enormous, print it modulo $998244353$.

Constraints

$N$ and $L$ are integers.
$1 \le N \le 18$
$1 \le L \le 10^9$
$S_i$ is a (not necessarily contiguous) non-empty subsequence of abcdefghijklmnopqrstuvwxyz.

Input

Input is given from Standard Input in the following format:

$N$ $L$
$S_1$
$S_2$
$\dots$
$S_N$

Output

Print the answer.

Sample Input 1

2 2
ab
ac

Sample Output 1

7

We can enter seven strings: aa, ab, ac, ba, bb, ca, cc.

Sample Input 2

4 3
abcdefg
hijklmnop
qrstuv
wxyz

Sample Output 2

1352

Sample Input 3

5 1000000000
abc
acde
cefg
abcfh
dghi

Sample Output 3

346462871

Be sure to print the answer modulo $998244353$.

我的笔记

容斥原理

我们要求 $|A\cup B\cup C|$，可以先求 $|A|+|B|+|C|$，发现有三个重复部分，那就再减去 $|A\cap B|,|B\cap C|,|A\cap C|$，发现减多了一个部分，那就再补回去一个 $|A\cap B\cap C|$

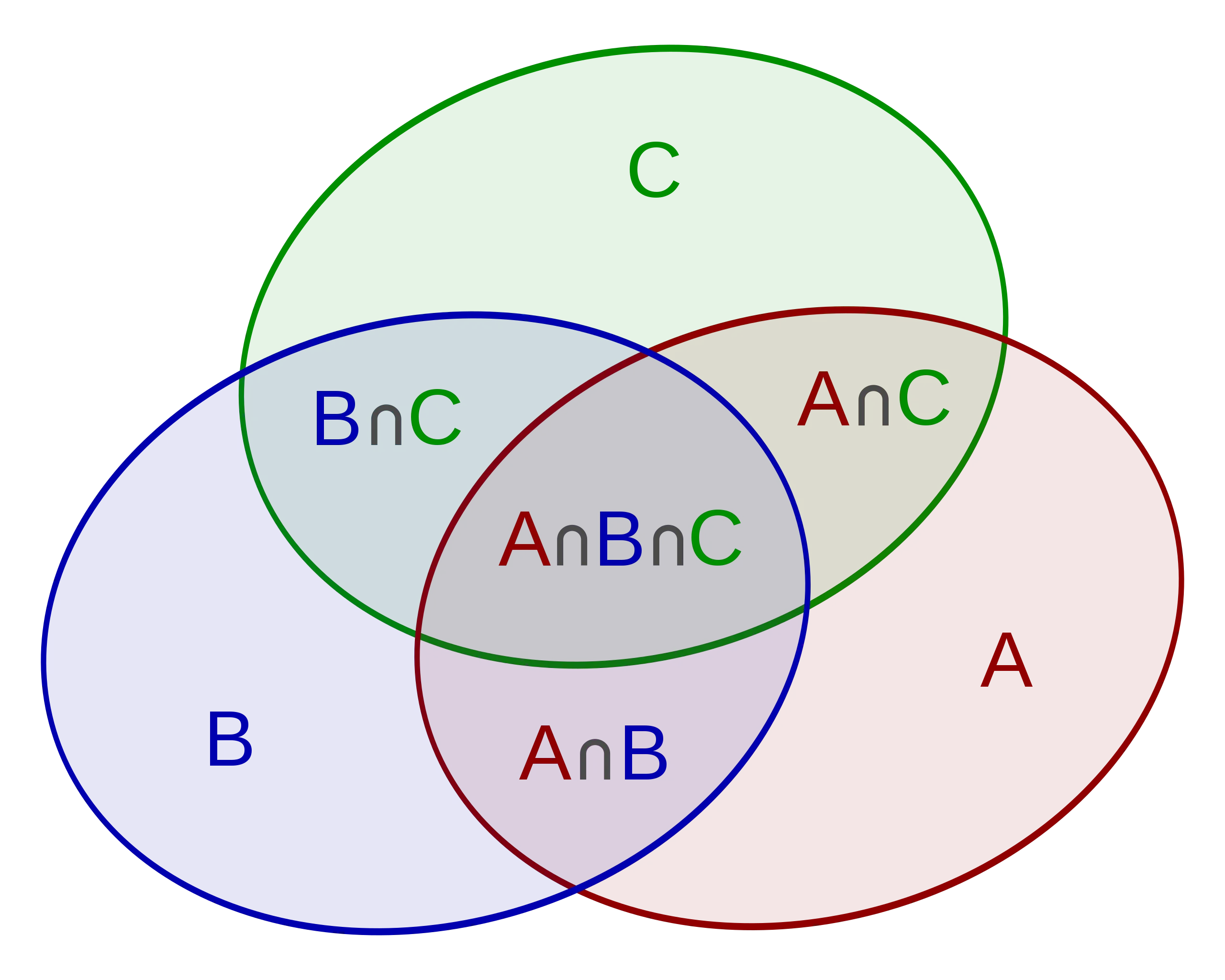
用数学语言描述容斥原理如下：

$$ {\displaystyle {\begin{aligned}\left|\bigcup _{i=1}^{n}A_{i}\right|={}&\sum _{i=1}^{n}|A_{i}|-\sum _{1\leq i<j\leq n}|A_{i}\cap A_{j}|+\sum _{1\leq i<j<k\leq n}|A_{i}\cap A_{j}\cap A_{k}|-\cdots +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|.\end{aligned}}} $$

（图片和公式来源：维基百科，使用 CC BY-NC-SA 4.0 许可）

题目转化

题目要求第 $1\sim N$ 行按键每行分别能组合出的长为 $L$ 的字符串的种数（后面简称种数）之和，便可以通过容斥原理转化为：（以 $N=3$ 为例）

$+$ 第 $1$ 行按键的种数 $+$ 第 $2$ 行按键的种数 $+$ 第 $3$ 行按键的种数

$-$ 第 $1、2$ 行按键都能组合出的种数 $-$ 第 $1、3$ 行按键都能组合出的种数 $-$ 第 $2、3$ 行按键都能组合出的种数

$+$ 第 $1、2、3$ 行按键都能组合出的种数

这所有情况加起来为 $2^{N}-1$ 种（因为 $2^{n} =\sum_{r=0}^{n}{C_{n}^{r}}$，减一是因为去除不选任何行的情况）

求种数

如果我们知道，第 $1$ 行按键有 $3$ 个不同的字母，如果要组成长为 $L$ 的字符串，那么种类就是 $3^L$

如果我们知道，第 $1、2$ 行按键有 $2$ 个都包含的字母，这两行按键都能组合出来的字符串的总数便是 $2^L$

因此不需要知道具体有那几个字母，只需知道字母个数即可。

位运算的巧妙

官方题解位运算更巧妙，不过我看着不习惯，还是换成了数组。运行时长长了 $30\%$ 左右，但是 AC 也是绰绰有余。

这里只说一个我觉得挺好的用法，就是 36 行的 for (int i = 1; i < (1 << N); i++) 和 43 行的 if (i & (1 << j))

前者用二进制的方法，只用了一个 for 循环就完成了容斥定理选 $1、2、\cdots、1和2、1和3、\cdots、1和2和3、\cdots$ 的操作。

选择方法是 $i$ 的第 $j$ 个二进制位为 $1$ 的时候就选第 $j+1$ 行，if 内用的 i & (1 << j) 便是这个目的

源码

#include <bits/stdc++.h>
#define MOD 998244353

using namespace std;

long long fast_pow(long long a, long long b)
{
    a %= MOD;
    long long ans = 1;
    while (b)
    {
        if (b % 2)
        {
            ans = ans * a % MOD;
        }
        b /= 2;
        a = a * a % MOD;
    }
    return ans;
}

int main()
{
    int N, L;
    cin >> N >> L;
    bool row[18][26];
    memset(row, false, sizeof(row));
    for (int i = 0; i < N; i++)
    {
        string keys;
        cin >> keys;
        for (auto &key : keys)
            row[i][key - 'a'] = true;
    }
    long long ans = 0;
    for (int i = 1; i < (1 << N); i++)
    {
        bool these_rows[26];
        memset(these_rows, true, sizeof(these_rows));
        int selected_row_cnt = 0, selected_key_cnt = 0;
        for (int j = 0; j < N; j++)
        {
            if (i & (1 << j))
            {
                selected_row_cnt++;
                for (int k = 0; k < 26; k++)
                {
                    these_rows[k] &= row[j][k];
                }
            }
        }
        for (int i = 0; i < 26; i++)
        {
            if (these_rows[i])
                selected_key_cnt++;
        }
        if (selected_row_cnt % 2)
        {
            ans += fast_pow(selected_key_cnt, L);
            ans %= MOD;
        }
        else
        {
            ans += MOD - fast_pow(selected_key_cnt, L);
            ans %= MOD;
        }
    }
    cout << ans << endl;
    return 0;
}

题目 | typewriter