检定素数的算法：埃氏筛 (埃拉托斯特尼筛法, Sieve of Eratosthenes)、欧拉筛 (线性筛, Euler's sieve)

埃氏筛

复杂度

• 时间复杂度：$O(n\log \log n)$
• 空间复杂度：$O(n)$

$n$ 为计算范围

代码实现

结果为一个范围从 $0\sim \text{MAXN}$ 的 bool 数组 is_prime，每一位储存该数字是否是素数。

const int MAXN = 1e5 + 10;
bool is_prime[MAXN]; // is_prime储存该数是否为素数

void init_prime()
{
    memset(is_prime, true, sizeof(is_prime));
    is_prime[0] = is_prime[1] = false; // 特判0、1不是素数
    for (int i = 2; i < MAXN; i++)     // 使用埃氏筛处理>1的情况
        if (is_prime[i])
            for (int j = 2; j * i < MAXN; j++)
                is_prime[i * j] = false;
}

算法分析

原理

从 $2$ 开始，如果该数为素数，就筛掉这个数的所有倍数。

这个思路非常简单易懂，因此埃氏筛比下面要讲的欧拉筛好写。

举例

$2$ 筛除 $4、6、8、10、12、14、16\cdots$
$3$ 筛除 $6、9、12、15、18、21、24\cdots$
$4$ 是合数，不筛除其他数字
$5$ 筛除 $10、15、20、25、30、35、40\cdots$
$⋮$

欧拉筛

时间复杂度

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

$n$ 为计算范围

代码实现

结果为一个下标 $0\sim \text{MAXN}$ 的 bool 数组 not_prime，每一位储存该数字是否不是素数。一个下标 $0\sim \text{primesize}$ 的 int 数组 prime，里面从小到大存放着范围 $[0,\text{MAXN}]$ 的素数。

为什么这里使用 not_prime 而不是 is_prime，其实只是为了省去全部 memset 为 true 的时间，加快效率。不过实际也不会有很大的效率区别，如果自己不习惯的话可以也改成 is_prime 版本。

// prime储存素数序列，primesize即素数数量，not_prime储存该数是否不是素数
const int MAXN = 1e5 + 10;
int prime[MAXN], primesize = 0;
bool not_prime[MAXN];

void init_prime()
{
    not_prime[0] = not_prime[1] = true; // 特判0、1不是素数
    for (int i = 2; i < MAXN; i++)      // 使用欧拉筛处理>1的情况
    {
        if (!not_prime[i])
            prime[primesize++] = i;
        for (int j = 0; j < primesize && i * prime[j] < MAXN; j++)
        {
            not_prime[i * prime[j]] = true;
            if (i % prime[j] == 0)
                break;
        }
    }
}

算法分析

埃氏筛会将一个数多次筛除，如 $30$ 会被 $2,3,5$ 筛除三次，浪费一定的时间。
欧拉筛只会用该数的最小质因子筛除该数，例如 $30$ 只会被 $2$ 筛除一次，节约时间。

该算法的灵魂就是每一步停止筛除的判断，对应到代码即 if (i % prime[j] == 0) break; 这一条。

原理

$\text{prime}$ 数组中的素数是递增的，当 $i$ 是 ${\text{prime}}_j$ 的倍数，那么 $i\times {\text{prime}}_{j+1}$ 这个合数肯定已经被 ${\text{prime}}_j$ 乘以某个数筛掉。因此当我们发现 $i$ 是 ${\text{prime}}_j$ 的倍数时，就可以 break 掉当前循环停止筛出。

简单证明如下：

因为 ${\text{prime}}_j\mid i$，即 $i={\text{prime}}_j\times k(k\in \mathbb{Z})$ ，那么：

$$i\times {\text{prime}}_{j+1}=({\text{prime}}_j\times k)\times {\text{prime}}_{j+1}=k^{\prime }\times {\text{prime}}_j$$

接下去的素数同理，所以不用筛下去了。

因此，在满足 ${\text{prime}}_j\mid i$ 这个条件之前以及第一次满足该条件时，${\text{prime}}_j$ 必定是 ${\text{prime}}_j\times i$ 的最小因子。

举例

模拟该算法的操作：从 $2$ 开始

• $2$ 为素数，将其加入 prime[ ]，当前 prime[1] = {2}

  • 筛除 $2\ast 2$
  • $2mod2=0$，停止筛除

• $3$ 为素数，将其加入 prime[ ]，当前 prime[2] = {2, 3}

  • 筛除 $3\ast 2$
  • 筛除 $3\ast 3$
  • $3mod3=0$，停止筛除

• $4$ 为合数

  • 筛除 $4\ast 2$
  • $4mod2=0$，停止筛除

• $5$ 为素数，将其加入 prime[ ]，当前 prime[3] = {2, 3, 5}

  • 筛除 $5\ast 2$
  • 筛除 $5\ast 3$
  • 到达 primesize，停止筛除

• $6$ 为合数

  • 筛除 $6\ast 2$
  • $6mod2=0$，停止筛除

​ $⋮$

就拿在 $4mod2=0$ 时停止筛除这个情况举例，当处于这个情况时，如果我们不停下，下一个要筛的就是 $4\times 3$，但是因为 $4$ 里面包含有 $2$，就说明 $4\times 3$ 一定能被 $2\times 6$ 筛去，再往后 $4\times 4$ 一定能被 $2\times 8$ 筛去，也就是当满足这个条件后，应当停止筛除。

时间复杂度对比

一个为 $O(n\log \log n)$，一个为 $O(n)$，虽说从时间复杂度上看，线性筛绝对占优势，如下图（假设底数为 $e$）

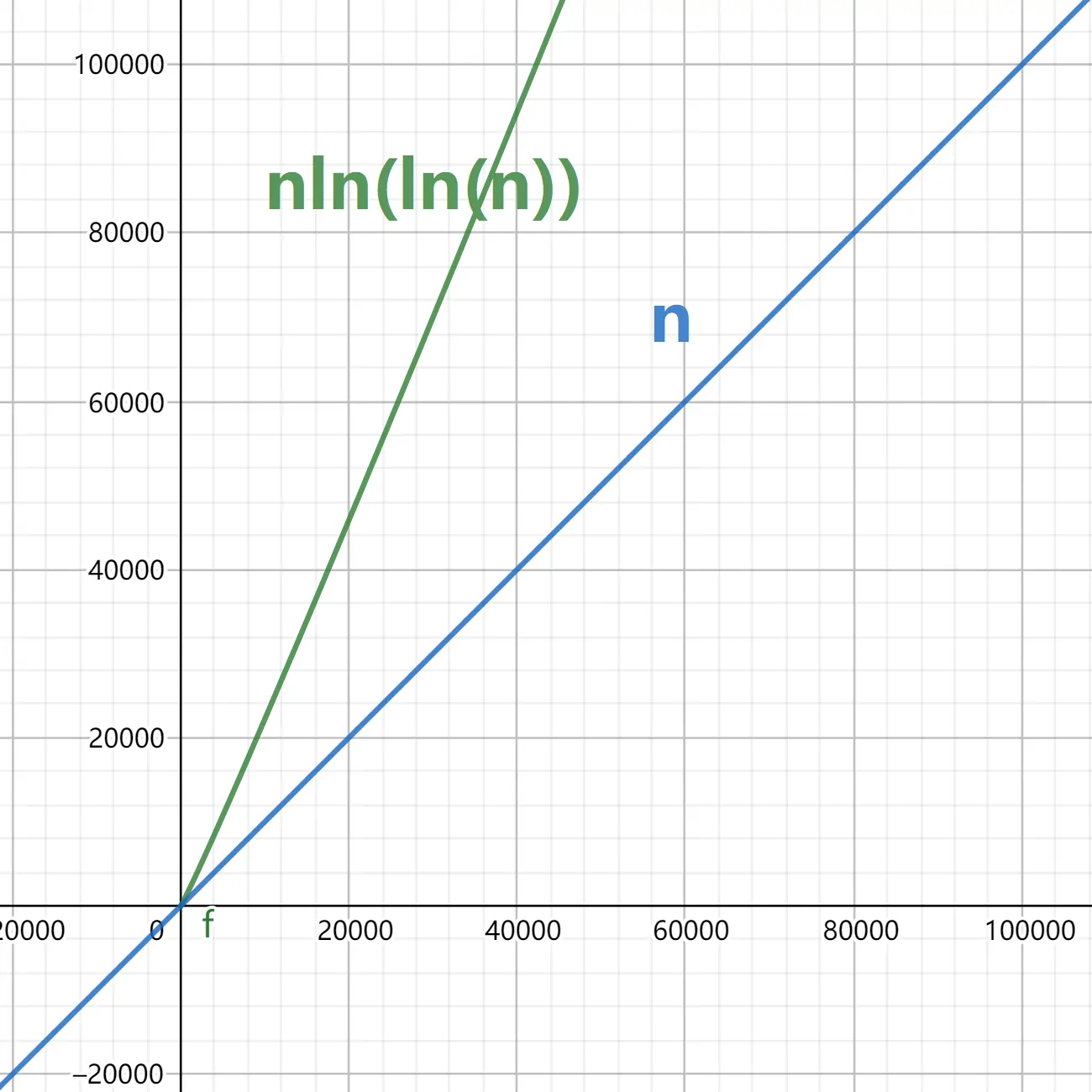
但在较小数据范围时，优势较小。而且线性筛内部包含有取模运算，在特定数据范围内可能速度不如埃氏筛。