在队列的基础上维护一个单调性的数据结构：单调队列 (Monotonic Queue)

在栈的基础上维护一个单调性的数据结构：单调栈 (Monotonic Stack)

单调队列

复杂度

时间复杂度：$O(n)$

空间复杂度：$O(n)$

（$n$ 为计算范围）

代码实现

STL 队列

// val[ ]: 储存数据的数组
// n: 需要计算的范围
// k: 给定的区间大小
// q: STL双向队列，储存val[ ]中元素的数组序号
deque<int> q;
for (int i = 0; i < n; i++)
{
    // 去尾操作
    while (!q.empty() && val[q.back()] > val[i])
        q.pop_back();
    // 新元素（的序号）入队
    q.push_back(i);
    // 判断是否需要进行下面两个操作
    if (i >= k - 1)
    {
        // 删头操作
        if (q.front() < i - k + 1)
            q.pop_front();
        // 输出操作
        cout << val[q.front()] << ' ';
    }
}

数组模拟队列

// val[ ]: 储存数据的数组
// n: 需要计算的范围
// k: 给定的区间大小
// q: 数组队列，储存val[ ]中元素的数组序号
// h, t: 队头、队尾指针，(0, -1)为空
int q[MAXN], h = 0, t = -1;
for (int i = 0; i < n; i++)
{
    while (h <= t && val[q[t]] > val[i])
        t--;
    q[++t] = i;
    if (i >= k - 1)
    {
        if (q[h] < i - k + 1)
            h++;
        cout << val[q[h]] << ' ';
    }
}

分析

（以单调递减序列为例）

流程：去尾操作 -> 入队操作 -> 删头操作 -> 输出操作 -> (循环)

去尾操作：

a. 若队列为空：直接跳到下一步

b. 若队列非空，若当前序号对应的数字比队尾小（即符合单调递减）：不去尾，跳到下一步

c. 若队列非空，若当前序号对应的数字比队尾小（不符合单调递减）：弹出队尾，再次比较，循环操作直到队尾符合条件或队列空

入队操作：

将当前数字对应的序号入队

（判断是否需要进行下面两个操作：当读取过的数据还没有k个时，不需要删头操作，也不需要输出）

删头操作：

a. 若队首（也就是队列最大值）还处于当前区间内：则队首对应的数字就是区间最大值，不删头，跳到下一步

b. 若队首（也就是队列最大值）处于当前区间外：弹出队首，再次比较，循环操作直到队首符合条件，此时队首对应的原数字就是区间最大值

输出操作：

输出队首序号对应到原数组中的数字，即当前区间最大值

例题

POJ2823 - Sliding Window: http://poj.org/problem?id=2823

单调栈

复杂度

时间复杂度：$O(n)$

空间复杂度：$O(n)$

（$n$ 为计算范围）

代码实现

STL 栈

// val[ ]: 储存数据的数组
// n: 需要计算的范围
// s: STL栈，储存val[ ]中元素的数组序号
stack<int> s;
for (int i = 0; i < n; i++)
{
    // 删除操作
    while (!s.empty() && val[s.top()] > val[i])
        s.pop();
    // 输出操作
    cout << (s.empty() ? -1 : val[s.top()]) << ' ';
    // 新元素（的序号）入队
    s.push(i);
}

数组模拟栈

// val[ ]: 储存数据的数组
// n: 需要计算的范围
// s: 数组栈，储存val[ ]中元素的数组序号
// t: 栈顶指针，0为空
int s[MAXN], t;
for (int i = 0; i < n; i++)
{
    while (idx && num[s[t]] >= num[i])
        t--;
    cout << (!t ? -1 : val[s[t]]) << ' ';
    s[++t] = i;
}

分析

与单调队列几乎一样，就是单调队列去掉了删头操作。

例题

POJ3250 - Bad Hair Day: http://poj.org/problem?id=3250

POJ2559 - Largest Rectangle in a Histogram: http://poj.org/problem?id=2559

二维单调队列

复杂度

时间复杂度：$O(n^2)$

空间复杂度：$O(n^2)$

（$n$ 为计算范围）

分析

对于二维情况，我们的思路就是，先用二维压缩为一维，再处理一维情况。核心思想就是，要求一个 $a\times b$ 的矩阵最小值，可以先将每行的最小值求出来，一共 $a$ 个数，然后再求这 $a$ 个数的最小值，得到的便是矩阵中的最小值。

以 $5\times5$ 的矩阵为例，我们要在其中求 $3\times3$ 的子矩阵的元素的最小值：

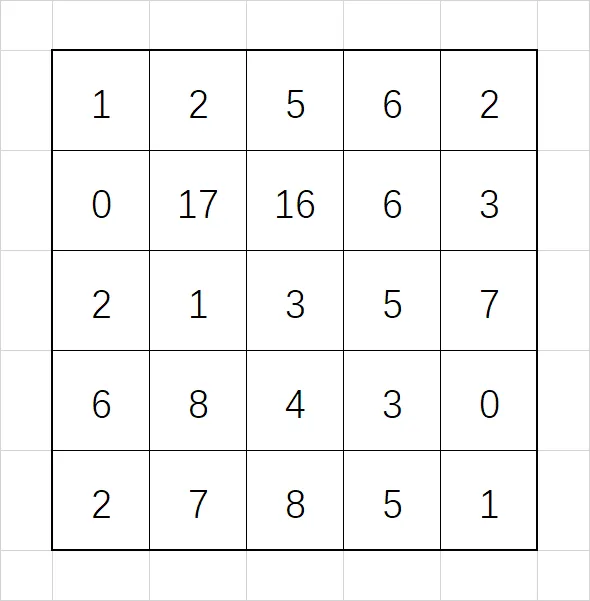
第一步，我们对每行分别使用单调队列求区间最小值，得到如下结果（灰色代表无意义数据）：

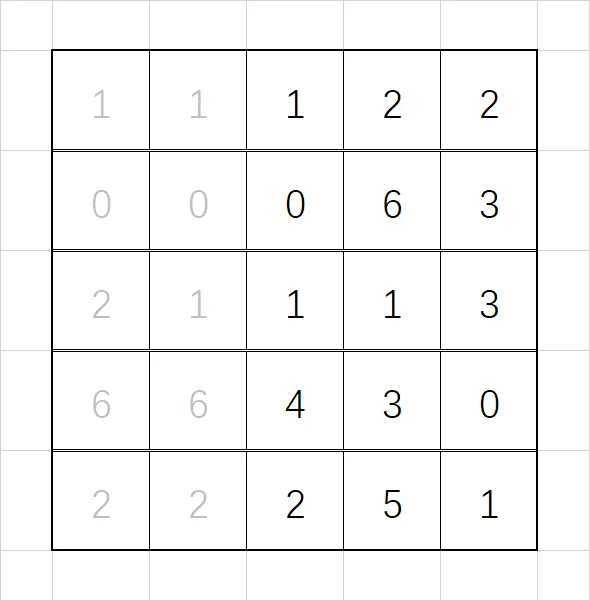
第二步，我们对每列分别使用单调队列求区间最小值，得到以下结果（灰色代表无意义数据）：

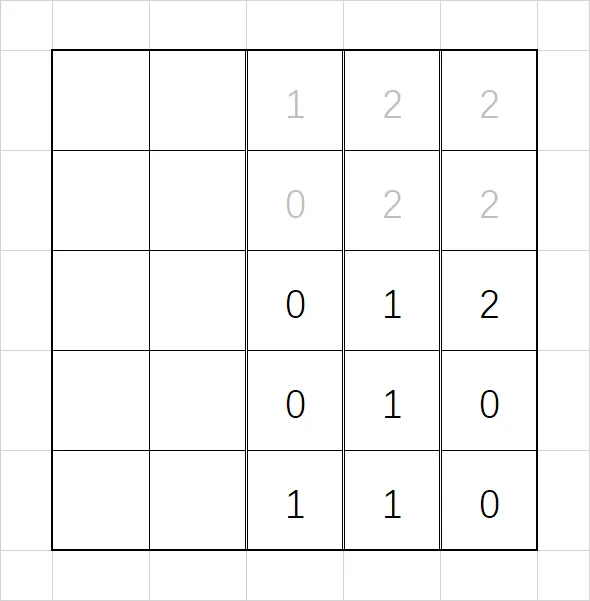
此时，第 $i$ 行第 $j$ 列的值就代表着，以 $(i,j)$ 为右下顶点的 $3\times3$ 子矩阵的最小值。

代码实现

与一维单调队列一致，只不过是使用了两次而已。

例题

AcWing 1091 - 理想的正方形: https://www.acwing.com/problem/content/description/1093/