搜索算法是利用计算机的高性能来有目的的穷举一个问题解空间的部分或所有的可能情况，从而求出问题的解的一种方法。

深度优先搜索 (Depth First Search, DFS)

广度优先搜索 (Breadth First Search, BFS)

深度优先搜索 (DFS)

搜索方式

深度优先搜索，从名字上来看就是搜索深度更优先的搜索方式。它会“执着”地走到头，只有无路可走时，它才会后退（回溯）一步，寻找新的路径。若用 DFS 来遍历下面这颗树，那么下图节点上的数字便是 DFS 遍历的先后顺序，我们接下来就具体描述下该顺序：

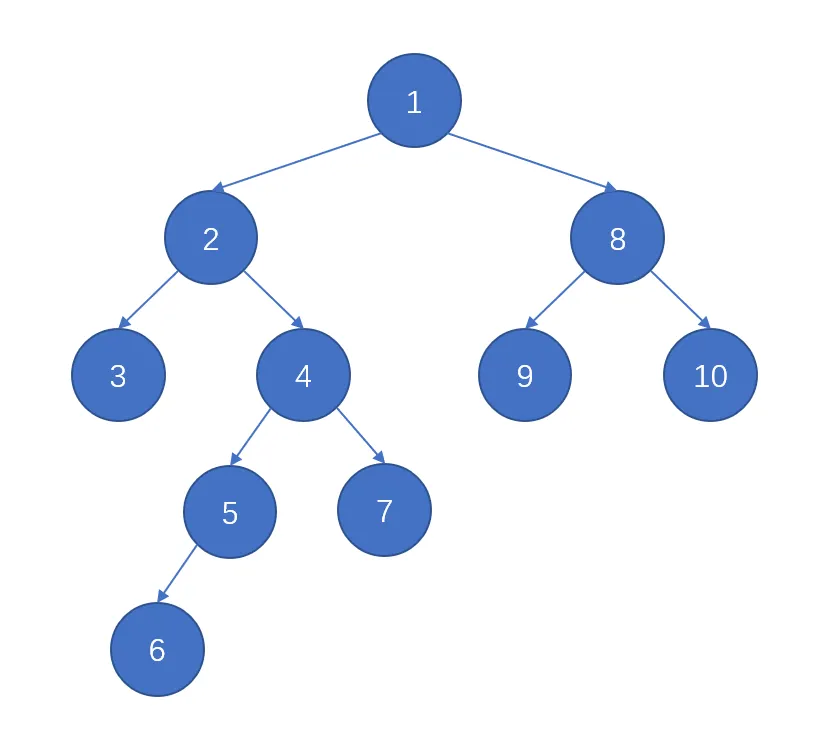
  • 向深搜索 $1\rightarrow2\rightarrow3$，无路可走。
  • 回溯一步 $2\leftarrow3$，有新的路线。
  • 向深搜索 $2\rightarrow4\rightarrow5\rightarrow6$，无路可走。
  • 回溯一步 $5\leftarrow6$，没有新路线，再回溯一步 $4\leftarrow5$，有新的路线。
  • 向深搜索 $4\rightarrow7$，无路可走。
  • 回溯一步 $4\leftarrow7$，没有新路线，再回溯一步 $2\leftarrow4$，没有新路线，再回溯一步 $1\leftarrow2$，有新的路线。
  • $\cdots\cdots$
  • 所有节点遍历完成

通过例子，我们大概已经明白 DFS 的搜索方式了。当然上面只是例子，DFS 能处理的并不只是树，也能够遍历图，原理是一样的。

时空复杂度

DFS 俗称暴力搜索，因为它遍历了所有可能情况，因此它的时间复杂度较高，能处理的数据规模较小。

但 DFS 每次搜索时只记录一条路径的信息，因此空间复杂度较低，为搜索深度。

代码模板

type dfs(type x, ... ) // 可以存在多个变量
{
    if( ... ) // 达成目标，找到答案
    {
        ... // 输出答案或判断最优解等等
        return;
    }
    if( ... ) // 达到搜索边界（即到边界了还没搜到，有时没有此步骤）
    {
        return;
    }
    for( ... ) // 遍历所有子节点
    {
        if( ... ) // 可以转移状态，一般用标志变量判断
        {
            ... // 修改标志变量，表明此节点不可转移
            dfs( ... ) // 搜索子节点，经常为x+1
            ... // 还原标志变量，表面此节点可转移
        }
    }
}

典型题型

洛谷P1706 - 全排列问题: https://www.luogu.com.cn/problem/P1706

洛谷P1219 - [USACO1.5]八皇后 Checker Challenge: https://www.luogu.com.cn/problem/P1219

广度优先搜索 (BFS)

搜索方式

广度（宽度）优先搜索，侧重点就在搜索的广度。它会搜索完当前深度的所有节点，才会深入一层，搜索下一层的节点。若用 BFS 来遍历下面这颗树，那么下图节点上的数字便是 BFS 遍历的先后顺序，我们接下来就具体描述下该顺序：

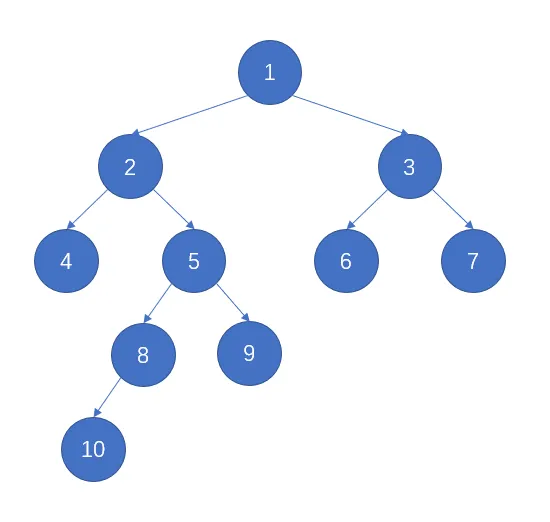
  • 遍历深度为 $1$ 的节点 $1$
  • 遍历深度为 $2$ 的节点 $2,3$
  • 遍历深度为 $3$ 的节点 $4,5,6,7$
  • 遍历深度为 $4$ 的节点 $8,9$
  • 遍历深度为 $5$ 的节点 $10$
  • 所有节点遍历完成

通过例子，我们大概已经明白 BFS 的搜索方式了。可以发现一个性质就是，如果路径长度为 $1$，BFS 遍历到的节点深度就等于距起点的距离。因此可以通过 BFS 处理一些最短路问题。

时空复杂度

BFS 也可以将所有情况遍历到，那么时间复杂度和 DFS 差不多。但 BFS 我们往往找到答案就会终止，并且可能更快找到答案，因此有时时间复杂度比 DFS 更好。

BFS 在每层遍历时需要保存该层所有节点，因此空间复杂度较高。

代码实现模板

bool vis[MAXN]; // 标记是否搜索过，有时也可直接用depth来判断
int depth[MAXN]; // 储存搜索深度，有时可能为二维数组或map
queue<type> que; // STL队列，不过数组模拟队列效率更高

type bfs(type start)
{
    que.push(start); // 起点入队
    depth[start] = 0; // 起点深度0
    vis[start] = true; // 标记起点
    while (!que.empty())
    {
        type now = que.front(); // 当前节点设置为队首
        que.pop(); // 弹出队首
        if ( ... ) // 如果达到目标条件
        {
            ans = depth[now]; // 储存答案
            return; // 搜索结束
        }
        for( ... ) // 遍历now节点的所有子节点，可用数组表示方向
        {
            type next = ... // 计算出子节点
            if (!vis[next] && ... ) // 如果子节点未搜索过，且范围符合题目条件
            {
                vis[next] = true; // 标记子节点
                depth[next] = depth[now] + 1; // 子节点深度+1
                que.push(next); // 子节点入队
                // 有时题目还需输出具体路径，可用一个数组储存每个节点的上一个节点，然后在此处对数组赋值。输出时，从结尾递归反向输出即可获得具体的路径。
            }
        }
    }
}

典型题型

POJ1077 - Eight: http://poj.org/problem?id=1077

POJ3984 - 迷宫问题: http://poj.org/problem?id=3984