机器学习 | LoRA
LoRA (Low-Rank Adaptation):一种模型微调方法,通过在预训练的深度学习模型中添加低秩矩阵,以实现更高效的参数更新和模型自适应。
本篇文章为论文笔记,图片截取自原论文。
1 背景
在大语言模型的应用中,往往先训练一个通用的预训练模型,再基于预训练模型进行垂直场景的微调。但大语言模型往往具有很高的参数量,例如 GPT-3 有 1750 亿的参数,如果对它做每个场景的微调,每个微调都要对所有参数进行优化,每个微调也得保存对应的微调参数,这样的训练计算量和储存需求量是不可接受的。
在这个背景下,一些优化方案被提出。例如向原模型中插入适配器层 (Adapter Layer),微调时仅更新适配器层的参数,保持预训练参数不变。这样每个微调只需要优化极少的适配器参数,每个微调也只需要保存适配器参数,降低了训练计算量和储存需求。但向原模型中插入适配器层,会导致模型变深,在 Batch Size 较小的推理场景下,会严重拖慢模型的推理速度。
LoRA 提出了一种新式的微调方案,通过添加低秩的适配器矩阵与原参数相加实现微调效果,低秩矩阵保证了训练计算量和储存需求量较低。同时简单的相加操作,使微调参数可以和预训练参数合并,合并后的模型与原模型结果完全一致,不影响推理速度。
2 LoRA
2.1 核心思想
对于全量微调方案,公式表示如下:
$$ \max_{\Phi}\sum_{(x,y)\in Z}\sum_{t=1}^{|y|}\log(P_{\Phi}(y_t|x,y_{<t})) $$
其中,$\Phi$ 代表预训练模型的参数,通过该公式可以看出我们要优化整个 $\Phi$ 来最大化模型的预测准确率。
对于 LoRA 微调方案,公式表示如下:
$$ \max_{\Theta}\sum_{(x,y)\in Z}\sum_{t=1}^{|y|}\log(P_{\Phi_0+\Delta\Phi(\Theta)}(y_t|x,y_{<t})) $$
其中,$\Theta$ 代表适配器的参数,通过该公式可以看出,通过适配器参数 $\Theta$ 决定了 $\Delta\Phi$,将其与预训练参数相加后则为模型的实际参数。我们要通过优化参数 $\Theta$ 来最大化模型的预测准确率。
2.2 方法细节
低秩更新
首先要注意 LoRA 中的 Low-Rank 含义,论文做出了一个重要的假设:下游微调任务对预训练参数 $W_0$ 做出的更新矩阵 $\Delta W$ 是低秩的。
$$ h=(W_0+\Delta W)x $$
在这个假设下,就可以对 $d\times d$ 的更新矩阵 $\Delta W$ 进行低秩分解,将其分解为 $d\times r$ 和 $r\times d$ 的两个投影矩阵 $B$ 和 $A$。其中 $r$ 可以取得很小,这样就能显著降低更新矩阵的参数量,即从 $d^2$ 降低到 $2dr$.
$$ \begin{align} &\begin{cases} h=(W_0+\Delta W)x\\ \Delta W_{d\times d}=B_{d\times r}A_{r\times d} \end{cases}\\ \Rightarrow &h=(W_0+BA)x \end{align} $$
初始化
然后需要注意 $B,A$ 的初始值,其中 $A$ 被初始化为均值 $0$ 方差 $\sigma^2$ 的高斯分布,$B$ 被初始化为零矩阵,因此初始情况下 $\Delta W=BA=\boldsymbol{0}$.
流程图
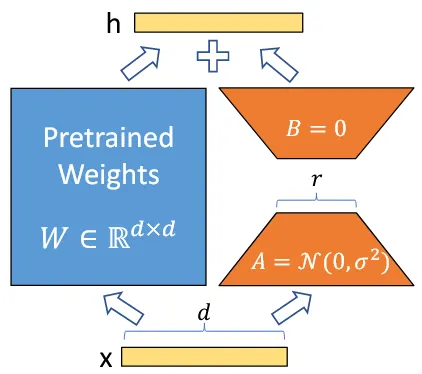
可合并
同时,注意到预训练参数 $W_0$ 和更新矩阵 $\Delta W$ 是进行的相加操作,根据矩阵乘法的分配律 $A\times(B+C)=A\times B+A\times C$,可以知道:
$$ h=(W_0+\Delta W)x=W_0x+\Delta Wx $$
即像上图流程一样将 $W_0$ 和 $\Delta W$ 拆开分别计算,和将 $W_0$ 和 $\Delta W$ 合并后计算式完全等价的。
那么,如果我们想要不额外引入计算代价,那么就完全可以将 LoRA 适配层与预训练权重合并,合并后的模型和原模型结构完全一致。但这样的代价就是得保存全部微调权重。
如果我们想要节省储存空间,那么就可以不合并权重,这样如果对一个预训练权重有多个微调,那么只需要保存一份原始权重和多个很小的 LoRA 适配权重,节省大量储存空间。
作用位置
最后,在 LoRA 应用于 Transformer 架构的 LLM 中时,论文提出的方法只向注意力参数添加适配层,即仅微调注意力参数 $Q,K,V,O$,而注意力层之间的多层感知机模块则不进行微调。
3 QLoRA
在模型推理中,量化技术可以使模型所需显存成倍降低,使小显存显卡也能运行大参数量的模型(虽然可能会非常慢),但量化技术并不能应用于模型微调中。
QLoRA 是 LoRA 技术的衍生技术,它将量化技术引入 LoRA 微调,使在不显著损失效果的情况下在 48G 显存显卡微调 650 亿参数大模型成为可能。它提出了三个重要方法:
- 4-bit 归一化浮点数量化 (4-bit NormalFloat Quantization)
- 双重量化 (Double Quantization)
- 页面优化 (Paged Optimizers)
3.1 归一化浮点数量化
首先了解一下分位数量化的流程:
- 将所有样本的数据进行排序,得到各自的 $2^k+1$ 分位数(只有 $2^k$ 个)。
- 将分位数编码为 $k$ 比特二进制数。
- 将所有样本映射到对应的分位数编码。
通过分位数编码,可以保证每个编码分组中数的数量相等,是信息论最优的数据类型。但可以发现它的开销很大,第一步的排序就有 $O(n\log n)$ 的复杂度。
归一化浮点数量化的思想基于分位数量化,它假定预训练神经网络的参数分布大多符合 $N(0,\sigma)$,那么就可以用正态分布的分位数来量化模型参数,绕开了高复杂度的排序操作。归一化浮点数量化的流程如下:
- 获取 $N(0,1)$ 分布的 $2^k+1$ 分位数。
- 将模型参数从 $N(0,\sigma)$ 归一化到 $N(0,1)$,即所有值在 $[-1,1]$ 范围。
- 接下来按照分位数量化的步骤操作即可。
下文 4 位归一化浮点数记作 NF4.
3.2 双重量化
可以注意到,上面提到的归一化浮点数量化会引入一个量化参数 $\sigma$(后面记作 $c_2$),如果对于一个 64 大小的量化块,使用 32 位浮点数储存 $c_2$,那么平均每个参数要多消耗 $32\text{bit}/64=0.5\text{bit}$ 空间,双重量化便是为了节省量化参数 $c_2$ 所需空间而提出的。
双重量化使用块大小 256,将原始 32 位浮点数量化到 8 位浮点数,同时又额外引入了一个 32 位浮点量化参数 $c_1$ 储存 $c_2$ 的均值。这样操作之后,平均每个参数要消耗 $8\text{bit}/64+32\text{bit}/(256\cdot 64)\approx0.127\text{bit}$,降低了约 $75\%$。
3.3 页面优化
这一点主要与硬件有关,用到了 NVIDIA 的统一内存特性,支持 CPU 和 GPU 之间的内存页面交换(就好像操作系统中内存与外存的页面交换).
3.4 总体形式
回顾原版的 LoRA 公式如下(添加了数据类型):
$$ y^{\text{BF16}}=W_0^{\text{BF16}}x^{\text{BF16}}+B^{\text{BF16}}A^{\text{BF16}}x^{\text{BF16}} $$
通过上面三个重要方法,QLoRA 的公式表示如下:
$$ y^{\text{BF16}}=\text{doubleDequant}(c_1^{\text{FP32}},c_2^{\text{k-bit}},W_0^{\text{NF4}})x^{\text{BF16}}+B^{\text{BF16}}A^{\text{BF16}}x^{\text{BF16}} $$
其中,双重量化的展开形式为:
$$ \text{doubleDequant}(c_1^{\text{FP32}},c_2^{\text{k-bit}},W_0^{\text{NF4}})=\text{dequant}(\text{dequant}(c_1^{\text{FP32}},c_2^{\text{k-bit}}),W_0^{\text{NF4}}) $$
可以注意到,QLoRA 的量化反而并不是作用于 LoRA,而是作用于预训练权重。这也好理解,因为 LoRA 模块大小非常小,模型参数主要还是来源于预训练权重,优化重点当然是预训练权重了。
4 AdaLoRA
LoRA 技术对所有层一视同仁设定了固定的秩,忽略了不同模块、不同层在微调任务中的重要性差异。给重要的层分配高秩,给次要的层分配低秩,把算力用到刀刃上,可以在权重大小不变的情况下提升模型效果。
AdaLoRA 是 LoRA 技术的衍生,它提出了一种动态调整模块分配的秩的方法,使算力得到合理分配。
4.1 奇异值分解
假设 $M$ 是一个 $m\times n$ 阶矩阵,其中的元素全部属于实数域或复数域。如此则存在一个分解使得:
$$ M=U\Sigma V^* $$
其中 $U$ 是 $m\times m$ 阶酉矩阵(即 $UU^*=I$),$\Sigma$ 是 $m\times n$ 阶非负实数对角矩阵,$V^*$ 是 $n\times n$ 阶酉矩阵,是 $V$ 的共轭转置。这样的分解就称作 $M$ 的奇异值分解。$\Sigma$ 对角线上的元素 $\Sigma_{i,i}$ 即为 $M$ 的奇异值。(来源:Wikipedia,使用 CC BY-SA 4.0 协议)
矩阵的奇异值代表了矩阵在线性变换过程中的缩放因子。具体来说,矩阵的奇异值可以告诉我们在矩阵作用下,原始空间中的向量会以多大的倍数进行缩放。这些奇异值按照大小排列,最大的奇异值对应的方向表示矩阵变换的主要方向,而较小的奇异值则表示次要方向上的缩放因子。
综上,矩阵的奇异值即可作为分配秩的依据,如果矩阵的某些奇异值非常小,就说明这些奇异值对矩阵效果的影响很小,将它们裁剪掉不会显著影响矩阵的效果。但是奇异值分解的代价昂贵,复杂度为 $O(\min(m^2n,mn^2)$,不可能在训练过程做这个操作。
4.2 近似操作
AdaLoRA 使用了一个巧妙的方法规避显式奇异值分解操作。首先回顾原版 LoRA 的增量矩阵:
$$ \Delta W=BA $$
在 AdaLoRA 中,增量矩阵被拆分为”奇异值分解“的形式:
$$ \Delta W=P\Lambda Q $$
拆分为该形式后,直接将参数交给优化器去训练,得到的结果就相当于进行了奇异值分解。其中 $\Lambda$ 初始化为 $0$,$P,Q$ 初始化为高斯分布。
不过有一点需要注意的是,奇异值分解要求 $P,Q$ 为酉矩阵(即 $PP^*=I$),优化器显然不会遵守这个限制。因此人工添加正则化参数来约束优化器:
$$ R(P,Q)=||P^{\mathrm{T}}P-I||_F^2+||QQ^{\mathrm{T}}-I||_F^2 $$
这个正则化参数挺好理解的,当 $P,Q$ 越近似于酉矩阵时损失值越小,因此让优化器能够尽量找到近似于酉矩阵的 $P,Q$ 参数。
4.3 评估重要性
通过近似奇异值分解后,就要评估每个奇异值的重要性了。
可以直接选用比较大小的方式,将奇异值的大小作为奇异值的重要性,裁剪掉最小的奇异值(即赋值为 $0$),保留大奇异值来减小矩阵秩。论文同时提出了另一种方法,估计当某个参数变为 $0$ 后损失函数值的变化。
同时需要注意的是,将奇异值赋值为 $0$ 在实际实现中,只是使用遮罩 (mask) 覆盖,并没有真正删除。这个操作是为了在错误删除后能够恢复,减小出错概率。
本文采用 CC BY-SA 4.0 许可,本文 Markdown 源码:Haotian-BiJi