树链剖 (pōu) 分：树链剖分用于将树分割成若干条链的形式，使它组合成线性结构，然后就可以用其他的数据结构（例如线段树）维护信息。

树链剖分

树链剖分有很多形式，本文介绍的为其中的重 (zhòng) 链剖分，下文树链剖分均指重链剖分。

1. 剖分方式

对于一棵树的一个节点，称它的子树最大的子节点为重子节点，其他子节点为轻子节点。特别的，树根看作轻子节点。

标记好轻重子节点后，从一个节点到它的重子节点连边，称这种边为重边，与它的轻子节点连边，这种边成为轻边。

由相接的重边构成的一条链便称为一条重链，通过上面描述的方法，即可将一棵树分成互不重复的重链。

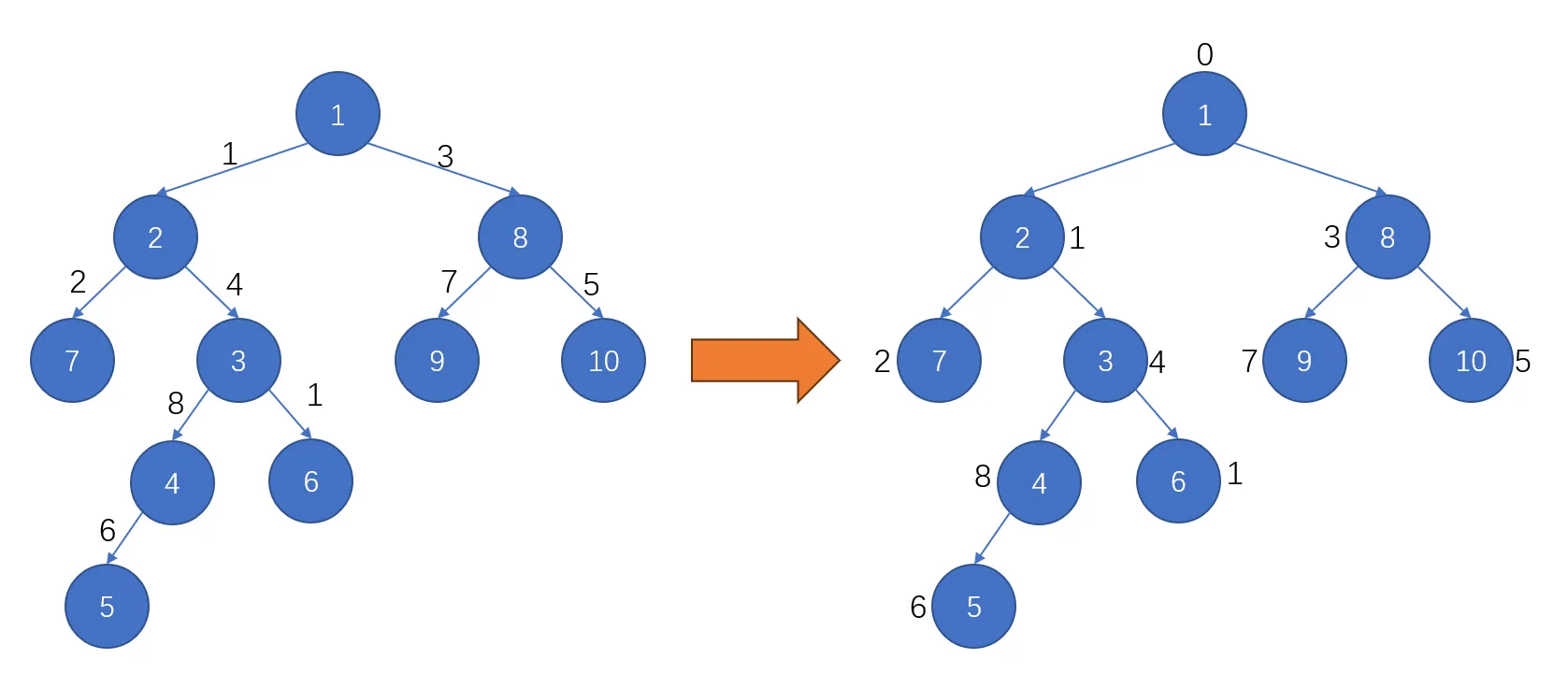
一个可视化的例子如下，右图中被绿框框住的便是分出的链：

图片来源：OI-Wiki
使用协议：CC BY-SA 4.0

2. 代码实现

要进行树链剖分，需要维护每个节点的以下信息：

节点深度 dep
父节点 fa
重子节点 son
子树大小 siz
所在重链的顶部节点 top
节点的 DFS 遍历序 dfn
DFS 序对于的节点编号 rnk，其为 dfn 的逆：$\mathrm{rnk}(\cdot)=\mathrm{dfn}^{-1}(\cdot)$

使用两次 DFS 生成上面的信息，第一次生成前 $4$ 个，第二次生成后 $3$ 个。DFS 的思路也比较好理解，直接看代码就能看懂。

注意：

DFS 遍历时，重边优先遍历。
代码中的树存的双向边，因此需要进行父节点判重。
代码中的树使用链式前向星储存，下标从 $1$ 开始。

void dfs1(int now)
{
    son[now] = -1;
    siz[now] = 1;
    for (int i = h[now]; i; i = ne[i])
    {
        int &nxt = e[i];
        if (nxt == fa[now])
            continue;
        fa[nxt] = now;
        dep[nxt] = dep[now] + 1;
        dfs1(nxt);
        siz[now] += siz[nxt];
        if (son[now] == -1 || siz[son[now]] < siz[nxt])
            son[now] = nxt;
    }
}

void dfs2(int now, int tp)
{
    top[now] = tp;
    dfn[now] = ++cnt;
    rnk[cnt] = now;
    if (son[now] == -1)
        return;
    dfs2(son[now], tp);
    for (int i = h[now]; i; i = ne[i])
    {
        int &nxt = e[i];
        if (nxt == son[now] || nxt == fa[now])
            continue;
        dfs2(nxt, nxt);
    }
}

3. 重链性质

树链剖分的目的就是将树型结构转为线性结构，从而可以套用线性数据结构解决问题。那么剖分出来的链一定要有一些独特的性质，方便对它套用线性数据结构。

每条链包含的节点不重不漏

树上的节点属于且仅属于一条重链，同时所有的重链将整棵树完全剖分。

同一重链内节点的 DFS 序连续

由于重边优先遍历，所以同一重链中的节点是 DFS 序是连续的。将节点按 DFN 排序后的序列就是剖分后的链。可以看上图中的绿色序号。

树上每条路径都可以拆分成不超过 $\log n$ 条重链

向下经过一条轻边时，所在子树大小至少 $\div 2$，因此对于树上任意一条路径，把它拆分成从 LCA 分别向两边往下走，最多走 $\log n$ 次。

4. 应用方式

4.1. 求最近公共祖先

要求查询两个节点的 LCA，那么每次让深度大的链往上跳，最后深度较小的节点就是 LCA。对于链的深度，定义为这个链的顶端节点的深度。

如果要查询 DFN 序为 $7,10$ 两个节点的 LCA：

$7$ 所在链的深度为 $6$，$10$ 所在链的深度为 $3$，因此 $7$ 往上跳到 $5$.
$5$ 所在链的深度为 $1$，$10$ 所在链的深度为 $3$，因此 $10$ 往上跳到 $2$.
发现 $2,5$ 处在同一个链上（检查链顶节点相同），此时浅的便是 LCA，即 $2$ 是 LCA.

int lca(int u, int v) 
{
    while (top[u] != top[v])
    {
        if (dep[top[u]] > dep[top[v]])
            u = fa[top[u]];
        else
            v = fa[top[v]];
    }
    return dep[u] > dep[v] ? v : u;
}

树链剖分解决 LCA 预处理的时间复杂度为 $O(n)$，查询的时间复杂度为 $O(\log n)$.

4.2. 路径上维护（权值在点上）

根据重链性质——同一重链内节点的 DFS 序连续，因此就可以用线段树或树状数组维护连续区间的信息，从而相当于维护了树上每一条路径的信息。下面用线段树维护树上路径的权值和举例。

建树

线段树数组中 $\text{sum}_i$ 储存的是用线段树维护的区间和，$\text{add\_val}_i$ 是线段树的加法懒惰标记，$w_i$ 是节点 $i$ 的权重。

首先建树时，向长度为 $1$ 的区间导入初始权值 $\text{sum}_i=w_{\mathrm{rnk}(i)}$，注意这里的对应关系，要用 $\mathrm{rnk}(i)$ 获取到 DFS 序为 $i$ 的节点编号。

int sum[MAXN], add_val[MAXN];
void build(int s, int t, int p)
{
    if (s == t)
    {
        sum[p] = w[rnk[s]];
        return;
    }
    int m = s + (t - s) / 2;
    build(s, m, p * 2);
    build(m + 1, t, p * 2 + 1);
    sum[p] = sum[p * 2] + sum[p * 2 + 1];
}

路径操作

用线段树维护树链时，线段树的代码是不需要变化的，需要改变的只是调用函数的方式。如果要对树上一条个路径进行操作，需要将其拆分为一条条链，然后分别对每一条链的区间进行操作，如果该操作是查询，那最后将每一条链的答案整合得到最终答案即可。

例如要对 DFS 序为 $7,15$ 两点的路径进行操作，那么将这条路径拆分成链：$7,1\sim5,11\sim12,15$ 这四条链，然后分别对这四条链进行操作，便是对 $7,15$ 两点的路径进行了操作。

那如何编写代码来找到要操作的链区间呢？我们的思路是每次深度大的链往上跳，向上跳的时候对刚才那条链进行操作。其实和上一节的求 LCA 一模一样，只不过现在在向上跳的同时要执行操作。

代码结构如下，对于具体的操作，下文也有对应代码：

int do_something(int a, int b)
{
    while (top[a] != top[b])
    {
        int ta = top[a], tb = top[b];
        if (dep[ta] >= dep[tb])
        {
            // do something in range [dfn[ta], dfn[a]]
            a = fa[ta];
        }
        else
        {
            // do something in range [dfn[tb], dfn[b]]
            b = fa[tb];
        }
    }
    if (dep[a] > dep[b])
        swap(a, b);
    // do something in range [dfn[a], dfn[b]]
    return ans;
}

路径区间查询

int query_sum(int a, int b)
{
    int ans = 0;
    while (top[a] != top[b])
    {
        int ta = top[a], tb = top[b];
        if (dep[ta] >= dep[tb])
        {
            ans += get_sum(dfn[ta], dfn[a], 1, n, 1);
            a = fa[ta];
        }
        else
        {
            ans += get_sum(dfn[tb], dfn[b], 1, n, 1);
            b = fa[tb];
        }
    }
    if (dep[a] > dep[b])
        swap(a, b);
    ans += get_sum(dfn[a], dfn[b], 1, n, 1);
    return ans;
}

下面用一个例子说明，如果要查询 DFN 序为 $7,13$ 两个节点的路径权值和：

$7$ 所在链的深度为 $6$，$13$ 所在链的深度为 $2$，因此 $7$ 往上跳到 $5$. 同时查询线段树区间 $7\sim7$ 的结果加入答案。
$5$ 所在链的深度为 $1$，$13$ 所在链的深度为 $2$，因此 $13$ 往上跳到 $1$. 同时查询线段树区间 $11\sim13$ 的结果加入答案。
发现 $1,5$ 处在同一个链上（检查链顶节点相同），查询线段树区间 $1\sim5$ 的结果加入答案，结束算法。

路径区间修改

这里用加法举例，其他其实也是完全一样的。

void add_to(int a, int b, int c)
{
    while (top[a] != top[b])
    {
        int ta = top[a], tb = top[b];
        if (dep[ta] >= dep[tb])
        {
            add(dfn[ta], dfn[a], c, 1, n, 1);
            a = fa[ta];
        }
        else
        {
            add(dfn[tb], dfn[b], c, 1, n, 1);
            b = fa[tb];
        }
    }
    if (dep[a] > dep[b])
        swap(a, b);
    add(dfn[a], dfn[b], c, 1, n, 1);
}

4.3. 路径上维护（权值在边上）

上一节的权值在每个点上，一条路径的权值和就是路径上每个点的和。但有些时候，给定的是边的权值，一条路径的权值是这条路径包含的边的权值和，此时就要做出一点调整。

首先需要调整的是第一个 DFS，它将一条边的边权赋给这条边深度较深的那个节点，将权值在边上的问题转换回了权值在点上的问题。这样就能套用原来的做法解决这个新问题了（根节点的权值为 $0$）.

下面代码中的第 12 行便是修改之处。

void dfs1(int now)
{
    son[now] = -1;
    siz[now] = 1;
    for (int i = h[now]; i; i = ne[i])
    {
        int &nxt = e[i];
        if (nxt == fa[now])
            continue;
        fa[nxt] = now;
        dep[nxt] = dep[now] + 1;
        val[nxt] = w[i]; // 将边权转化成子节点点权
        dfs1(nxt);
        siz[now] += siz[nxt];
        if (son[now] == -1 || siz[son[now]] < siz[nxt])
            son[now] = nxt;
    }
}

将权值转化到点上后，后面 build 函数建树时，就用 $\mathrm{val}_i$ 中的数据而不是边权数据 $w_i$ 了：

但是，此时如果沿用之前的路径操作，会出现问题。就以上面的示意图为例，如果要求 $6\leftrightarrow7$ 的路径权值和，那就会把 $6,3,2,7$ 四个点的权值加起来，但很明显 $2$ 号节点的权值是 $1\leftrightarrow2$ 这条边的，并不属于 $6\leftrightarrow7$ 的路径，此时发生了错误。

要解决这个错误实际上也很简单，就是在加上最后一条链时，将顶端那个点排除在外，这样就不会加入错误的边了。这样，路径操作的结构变为：（区别在倒数第三行）

int do_something(int a, int b)
{
    while (top[a] != top[b])
    {
        int ta = top[a], tb = top[b];
        if (dep[ta] >= dep[tb])
        {
            // do something in range [dfn[ta], dfn[a]]
            a = fa[ta];
        }
        else
        {
            // do something in range [dfn[tb], dfn[b]]
            b = fa[tb];
        }
    }
    if (dep[a] > dep[b])
        swap(a, b);
    // do something in range [dfn[a] + 1, dfn[b]]
    return ans;
}

算法 | 树链剖分